24.1.1 圆 课件(共19张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.1.1 圆 课件(共19张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
圆
24.1 圆的有关性质
课堂导航
理解并掌握圆的有关概念
能灵活运用圆的有关概念解决相关的实际问题
情景引入
观察 圆是常见的图形,生活中的许多物体都给我们以圆的形象
新知探究
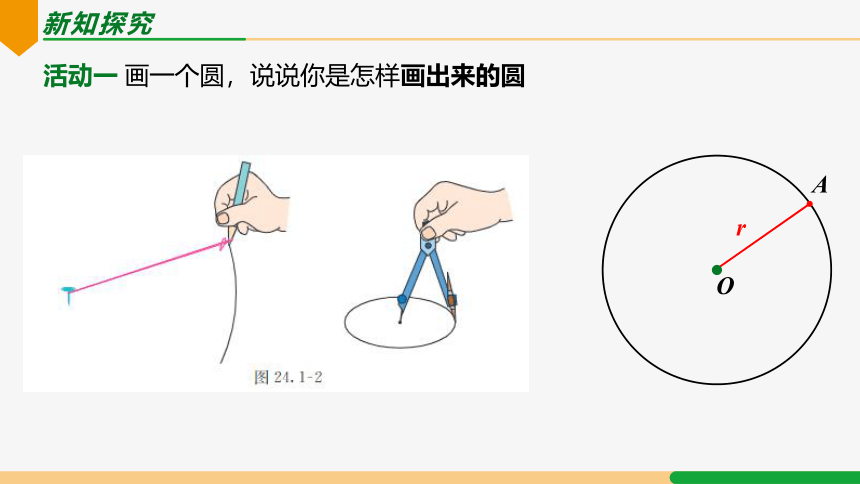
活动一 画一个圆,说说你是怎样画出来的圆
O
r
A
知识要点1
圆的定义1
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
其中,固定的端点O叫做圆心。
线段OA叫做半径。
以点O为圆心的圆,记作“⊙O”,读作“圆O”。
O
r
A
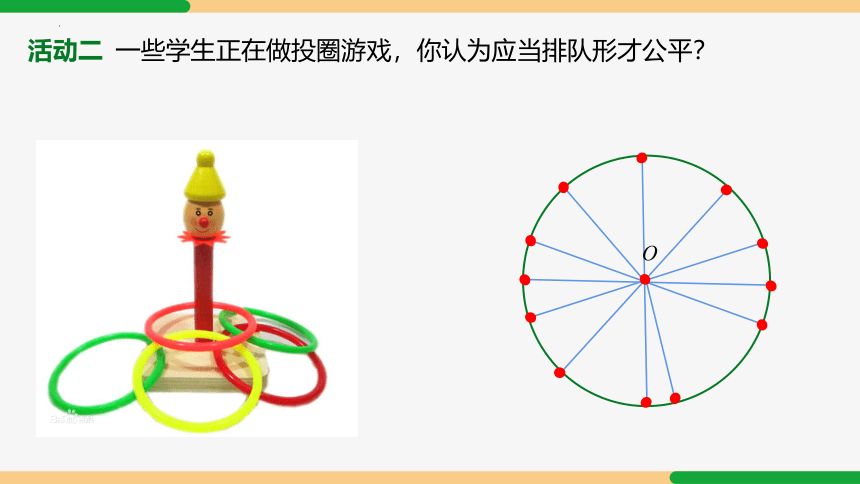
活动二 一些学生正在做投圈游戏,你认为应当排队形才公平?
O
2.到定点的距离等于定长的点都在同一个圆上。
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长 r的点组成的图形。
知识要点2
圆的定义2
O
r
A
1.圆上各点到定点(圆心O)的距离都等于定长(半径r);
经过圆心的弦(如图中的AB)叫做直径。
连接圆上任意两点的线段(如图AC)叫做弦。
·
C
O
A
B
直径都是弦,是圆中最长的弦,但弦不一定是直径。
·
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB ,读作“圆弧AB”或“弧AB”。
小于半圆的弧(如图中的AB)叫做劣弧;
大于半圆的弧(用三个字母表示,如图中的ACB)叫做优弧.
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆。
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧。
圆心相同,半径不相等的两个圆叫做同心圆。
能够互相重合的两个圆叫做等圆。
B
A
注意:1.半径相等的两个圆是等圆;
2.同圆或等圆的半径相等。
O
在同圆或等圆中,能够互相重合的弧叫做等弧。
针对练习
1 判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
典例讲解
例1 矩形 ABCD 的对角线 AC、BD 相交于点 O.
求证:A、B、C、D 四个点在以 O 为圆心的同一圆上.
A
B
C
D
O
证明:∵ 四边形 ABCD 是矩形,
∴ AO = OC,OB = OD.
又∵ AC = BD,
∴ OA = OB = OC = OD.
∴ A、B、C、D 在以 O 为圆心, OA 为半径的圆上.
例2 . 如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若∠AOC = 70°,且 AD∥OC,求∠AOD 的度数.
解:∵AD∥OC,
∴∠DAO =∠AOC = 70°.
又∵OD = OA,
∴∠ADO =∠DAO = 70°.
∴∠AOD = 180-70°-70° = 40°.
课堂小结
定义
圆
有关概念
弦
弧
直径是圆中最长的弦
半圆
优弧:大于半圆的弧
劣弧:小于半圆的弧
等圆或同圆
等弧
旋转定义
集合定义
O
r
A
·
C
O
A
B
课堂练习
1. 以下命题:
(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径;
(4)直径是圆中最长的弦;
(5)直径不是弦;
(6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
2. 填空:
(1)______是圆中最长的弦,它是______的 2 倍.
(2)图中有 条直径, 条非直径的弦,
圆中以 A 为一个端点的优弧有 条,劣弧有 条.
直径
半径
1
2
4
4
A
B
C
D
O
F
E
3.已知:如图,在⊙O中,AB为弦,C、D两点在 AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO.
∴OC=OD.
4. 如图,MN 是半圆 O 的直径,正方形 ABCD 的顶点 A、D 在半圆上,顶点 B、C 在直径 MN 上.
(1) 求证:OB = OC;
(2) 设⊙O 的半径为 10,求正方形 ABCD 的边长
证明:如图,连接 OA,OD,
则 OA = OD.
∵ 四边形 ABCD 是正方形,
∴ AB = CD,∠ABO =∠DCO = 90°.
∴ Rt△ABO≌Rt△DCO(HL).
∴ OB = OC.
在 Rt△ABO 中,AB2 + BO2 = AO2,
即 (2x)2 + x2 = 102.
(2) 设⊙O 的半径为 10,求正方形 ABCD 的边长
解析:设 OB = x,
则 AD = BC = OB + OC = 2x.
解得 x = (舍去负值)
∴ 正方形 ABCD 的边长为 2x =
圆
24.1 圆的有关性质
课堂导航
理解并掌握圆的有关概念
能灵活运用圆的有关概念解决相关的实际问题
情景引入
观察 圆是常见的图形,生活中的许多物体都给我们以圆的形象
新知探究
活动一 画一个圆,说说你是怎样画出来的圆
O
r
A
知识要点1
圆的定义1
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆。
其中,固定的端点O叫做圆心。
线段OA叫做半径。
以点O为圆心的圆,记作“⊙O”,读作“圆O”。
O
r
A
活动二 一些学生正在做投圈游戏,你认为应当排队形才公平?
O
2.到定点的距离等于定长的点都在同一个圆上。
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长 r的点组成的图形。
知识要点2
圆的定义2
O
r
A
1.圆上各点到定点(圆心O)的距离都等于定长(半径r);
经过圆心的弦(如图中的AB)叫做直径。
连接圆上任意两点的线段(如图AC)叫做弦。
·
C
O
A
B
直径都是弦,是圆中最长的弦,但弦不一定是直径。
·
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB ,读作“圆弧AB”或“弧AB”。
小于半圆的弧(如图中的AB)叫做劣弧;
大于半圆的弧(用三个字母表示,如图中的ACB)叫做优弧.
圆的任意一条直径的两个端点把圆分成的两条弧,每一条弧都叫做半圆。
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧。
圆心相同,半径不相等的两个圆叫做同心圆。
能够互相重合的两个圆叫做等圆。
B
A
注意:1.半径相等的两个圆是等圆;
2.同圆或等圆的半径相等。
O
在同圆或等圆中,能够互相重合的弧叫做等弧。
针对练习
1 判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(7)圆心相同,半径相等的两个圆是同心圆;
(8)半径相等的两个圆是等圆.
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
典例讲解
例1 矩形 ABCD 的对角线 AC、BD 相交于点 O.
求证:A、B、C、D 四个点在以 O 为圆心的同一圆上.
A
B
C
D
O
证明:∵ 四边形 ABCD 是矩形,
∴ AO = OC,OB = OD.
又∵ AC = BD,
∴ OA = OB = OC = OD.
∴ A、B、C、D 在以 O 为圆心, OA 为半径的圆上.
例2 . 如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,且点 C、D 在 AB 的异侧,连接 AD、OD、OC.若∠AOC = 70°,且 AD∥OC,求∠AOD 的度数.
解:∵AD∥OC,
∴∠DAO =∠AOC = 70°.
又∵OD = OA,
∴∠ADO =∠DAO = 70°.
∴∠AOD = 180-70°-70° = 40°.
课堂小结
定义
圆
有关概念
弦
弧
直径是圆中最长的弦
半圆
优弧:大于半圆的弧
劣弧:小于半圆的弧
等圆或同圆
等弧
旋转定义
集合定义
O
r
A
·
C
O
A
B
课堂练习
1. 以下命题:
(1)半圆是弧,但弧不一定是半圆;
(2)过圆上任意一点只能作一条弦,且这条弦是直径;
(3)弦是直径;
(4)直径是圆中最长的弦;
(5)直径不是弦;
(6)优弧大于劣弧;
(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
2. 填空:
(1)______是圆中最长的弦,它是______的 2 倍.
(2)图中有 条直径, 条非直径的弦,
圆中以 A 为一个端点的优弧有 条,劣弧有 条.
直径
半径
1
2
4
4
A
B
C
D
O
F
E
3.已知:如图,在⊙O中,AB为弦,C、D两点在 AB上,且AC=BD.
求证:OC=OD.
证明:∵OA、OB为⊙O的半径,
∴OA=OB. ∴∠A=∠B.
又∵AC=BD,
∴△ACO≌△BDO.
∴OC=OD.
4. 如图,MN 是半圆 O 的直径,正方形 ABCD 的顶点 A、D 在半圆上,顶点 B、C 在直径 MN 上.
(1) 求证:OB = OC;
(2) 设⊙O 的半径为 10,求正方形 ABCD 的边长
证明:如图,连接 OA,OD,
则 OA = OD.
∵ 四边形 ABCD 是正方形,
∴ AB = CD,∠ABO =∠DCO = 90°.
∴ Rt△ABO≌Rt△DCO(HL).
∴ OB = OC.
在 Rt△ABO 中,AB2 + BO2 = AO2,
即 (2x)2 + x2 = 102.
(2) 设⊙O 的半径为 10,求正方形 ABCD 的边长
解析:设 OB = x,
则 AD = BC = OB + OC = 2x.
解得 x = (舍去负值)
∴ 正方形 ABCD 的边长为 2x =
同课章节目录
