24.1.2 垂直于弦的直径 课件(共22张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 24.1.2 垂直于弦的直径 课件(共22张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 26.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 06:04:58 | ||
图片预览







文档简介
(共22张PPT)
垂直于弦的直径
24.1 圆的有关性质
课堂导航
理解圆的轴对称性及垂径定理的推导
能初步应用垂径定理进行计算和证明
新知探究
O
活动一:思考圆是轴对称图形吗?你怎样得出这个结论?你还发现了什么呢?
知识要点1
圆的对称性
圆是轴对称图形,任何一条直径所在直线都是它的对称轴
O
圆的对称轴是任意一条过圆心的直线
A
试证:圆是轴对称图形,任何一条直径所在直线都是它的对称轴
O
A′
M
·
O
A
A′
C
D
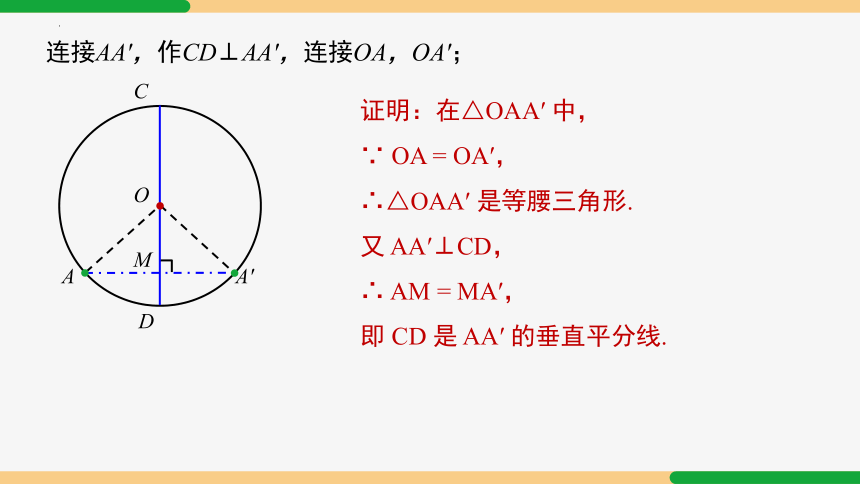
连接AA′,作CD⊥AA′,连接OA,OA′;
证明:在△OAA′ 中,
∵ OA = OA′,
∴△OAA′ 是等腰三角形.
又 AA′⊥CD,
∴ AM = MA′,
即 CD 是 AA′ 的垂直平分线.
知识要点2
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
A′
C
D
M
∵ CD 是⊙O 的直径,CD⊥AA′,(条件)
∴AM = A′M,
(结论)
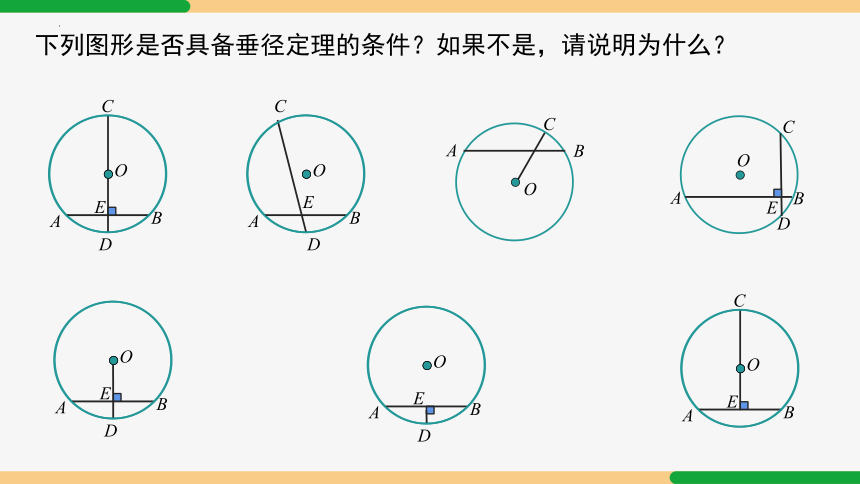
下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
O
A
B
C
A
B
D
C
O
E
A
B
O
C
D
E
A
B
O
C
D
E
A
B
O
D
E
A
B
O
C
E
E
A
B
O
D
知识要点3
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵ AM = A′M,CD 是⊙O 的直径
∴CD⊥AA′,
·
O
A
A′
C
D
M
·
O
A
B
C
D
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦 (不是直径)
(4)这条直线平分 (不是直径)弦所对的优弧
(5)这条直线平分 (不是直径)弦所对的劣弧
活动三:垂径定理及推论的规律
任意两条件
其余三结论
知二得三
·
O
A
A′
C
D
M
典例讲解
例1 如图,OE⊥AB 于 E,若⊙O 的半径为 10 cm,OE = 6 cm,求 AB的长
·
O
A
B
E
解析:连接 OA.
∴ AB = 2AE = 16 (cm).
∵ OE⊥AB,
例2 赵州桥是我国隋代建造的石拱桥,距今约有 1400 年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
由垂径定理,得 AD = AB = 18.5 ,
设⊙O 的半径为 R m.
在 Rt△AOD 中,
AO = R,OD = R - 7.23,AD = 18.5.
由勾股定理,得AO2=OD2+DB2
解得 R ≈ 27.3.
即赵州桥主桥拱的半径约为 27.3 m.
∴ R2 = (R - 7.23)2 + 18.52,
解:如图,过桥拱所在圆的圆心 O 作 AB 的垂线,交 于点 C,交弦 AB 于点 D,则 CD = 7.23.
知识要点4
垂径定理的应用
垂径定理转化直角三角形中应用勾股定理来解决
·
·
O
A
B
E
C
半径、弦长、弦心距、弓形高
(知二求二)
例3 求下列圆弧的圆心
A
B
课堂小结
轴对称图形
垂径定理
定理
推论
方法
垂直于弦的直径平分这条弦,并且平分弦所对两条的弧.
两条辅助线:连半径,作弦心距
构造直角三角形,利用勾股定理,建立方程.
思路
(1)直线过圆心;(2)垂直于弦;(3)平分弦;
(4)平分优弧;(5)平分劣弧 (弦不是直径)
·
O
A
B
E
C
对称
知二得三
方程思想
构造
对折
课堂练习
1.如图,在 O中,AB=8,OA=5,则OE= ,ED= .
2.如图,在 O中,OA=5,ED=2,则OE= ,AB= .
3.如图,在 O中,AB=8,ED=2,则OA= ,OE= .
3
2
3
8
3
5
5.已知⊙O 的半径为 10 cm,弦 MN ∥EF,且 MN = 12 cm,EF = 16 cm,则弦 MN 和 EF 之间的距离为 cm.
14 或 2
4. 如图 a、b,一弓形弦长为 cm,弓形所在的圆的半径为 7 cm,则弓形的高为________cm.
C
图 b
D
C
B
O
A
D
O
A
B
图 a
2 或 12
5.如图,⊙M 与x轴交于A,B 两点,与y轴交于C,D 两点,若M(2,0),B(5,0),则C点的坐标是 .
·
O
A
B
M
C
D
x
y
6.如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面AB宽度
【详解】连接OA,
∵桥拱半径OC为5m,∴OA=5m,
∵CD=8m,∴OD=8 5=3(m),
∴AD= (m)
∴AB=2AD=2×4=8(m),故选D.
圆管涵是公路路基排水中常用的涵洞结构类型,它不仅力学性能好,且构造简单、施工方便.某水平放置的圆管涵圆柱形排水管道的截面是直径为 1 m 的圆,如图所示,若水面宽 AB = 0.8 m,求水的最大深度.
解:如图,作 OC⊥AB 于点 C,连接 OA,
∴∠ACO = 90°, AC = AB.
∵ AB = 0.8 m,
∴ AC = 0.4 m.
∵ 直径为 1 m,∴ OA = 0.5 m.
在 Rt△AOC 中,根据勾股定理,得
∴ 0.3 + 0.5 = 0.8 (m).
∴ 水深的最大深度为 0.8 m.
垂直于弦的直径
24.1 圆的有关性质
课堂导航
理解圆的轴对称性及垂径定理的推导
能初步应用垂径定理进行计算和证明
新知探究
O
活动一:思考圆是轴对称图形吗?你怎样得出这个结论?你还发现了什么呢?
知识要点1
圆的对称性
圆是轴对称图形,任何一条直径所在直线都是它的对称轴
O
圆的对称轴是任意一条过圆心的直线
A
试证:圆是轴对称图形,任何一条直径所在直线都是它的对称轴
O
A′
M
·
O
A
A′
C
D
连接AA′,作CD⊥AA′,连接OA,OA′;
证明:在△OAA′ 中,
∵ OA = OA′,
∴△OAA′ 是等腰三角形.
又 AA′⊥CD,
∴ AM = MA′,
即 CD 是 AA′ 的垂直平分线.
知识要点2
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧
·
O
A
A′
C
D
M
∵ CD 是⊙O 的直径,CD⊥AA′,(条件)
∴AM = A′M,
(结论)
下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
O
A
B
C
A
B
D
C
O
E
A
B
O
C
D
E
A
B
O
C
D
E
A
B
O
D
E
A
B
O
C
E
E
A
B
O
D
知识要点3
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
∵ AM = A′M,CD 是⊙O 的直径
∴CD⊥AA′,
·
O
A
A′
C
D
M
·
O
A
B
C
D
(1)一条直线过圆心
(2)这条直线垂直于弦
(3)这条直线平分弦 (不是直径)
(4)这条直线平分 (不是直径)弦所对的优弧
(5)这条直线平分 (不是直径)弦所对的劣弧
活动三:垂径定理及推论的规律
任意两条件
其余三结论
知二得三
·
O
A
A′
C
D
M
典例讲解
例1 如图,OE⊥AB 于 E,若⊙O 的半径为 10 cm,OE = 6 cm,求 AB的长
·
O
A
B
E
解析:连接 OA.
∴ AB = 2AE = 16 (cm).
∵ OE⊥AB,
例2 赵州桥是我国隋代建造的石拱桥,距今约有 1400 年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
由垂径定理,得 AD = AB = 18.5 ,
设⊙O 的半径为 R m.
在 Rt△AOD 中,
AO = R,OD = R - 7.23,AD = 18.5.
由勾股定理,得AO2=OD2+DB2
解得 R ≈ 27.3.
即赵州桥主桥拱的半径约为 27.3 m.
∴ R2 = (R - 7.23)2 + 18.52,
解:如图,过桥拱所在圆的圆心 O 作 AB 的垂线,交 于点 C,交弦 AB 于点 D,则 CD = 7.23.
知识要点4
垂径定理的应用
垂径定理转化直角三角形中应用勾股定理来解决
·
·
O
A
B
E
C
半径、弦长、弦心距、弓形高
(知二求二)
例3 求下列圆弧的圆心
A
B
课堂小结
轴对称图形
垂径定理
定理
推论
方法
垂直于弦的直径平分这条弦,并且平分弦所对两条的弧.
两条辅助线:连半径,作弦心距
构造直角三角形,利用勾股定理,建立方程.
思路
(1)直线过圆心;(2)垂直于弦;(3)平分弦;
(4)平分优弧;(5)平分劣弧 (弦不是直径)
·
O
A
B
E
C
对称
知二得三
方程思想
构造
对折
课堂练习
1.如图,在 O中,AB=8,OA=5,则OE= ,ED= .
2.如图,在 O中,OA=5,ED=2,则OE= ,AB= .
3.如图,在 O中,AB=8,ED=2,则OA= ,OE= .
3
2
3
8
3
5
5.已知⊙O 的半径为 10 cm,弦 MN ∥EF,且 MN = 12 cm,EF = 16 cm,则弦 MN 和 EF 之间的距离为 cm.
14 或 2
4. 如图 a、b,一弓形弦长为 cm,弓形所在的圆的半径为 7 cm,则弓形的高为________cm.
C
图 b
D
C
B
O
A
D
O
A
B
图 a
2 或 12
5.如图,⊙M 与x轴交于A,B 两点,与y轴交于C,D 两点,若M(2,0),B(5,0),则C点的坐标是 .
·
O
A
B
M
C
D
x
y
6.如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,求水面AB宽度
【详解】连接OA,
∵桥拱半径OC为5m,∴OA=5m,
∵CD=8m,∴OD=8 5=3(m),
∴AD= (m)
∴AB=2AD=2×4=8(m),故选D.
圆管涵是公路路基排水中常用的涵洞结构类型,它不仅力学性能好,且构造简单、施工方便.某水平放置的圆管涵圆柱形排水管道的截面是直径为 1 m 的圆,如图所示,若水面宽 AB = 0.8 m,求水的最大深度.
解:如图,作 OC⊥AB 于点 C,连接 OA,
∴∠ACO = 90°, AC = AB.
∵ AB = 0.8 m,
∴ AC = 0.4 m.
∵ 直径为 1 m,∴ OA = 0.5 m.
在 Rt△AOC 中,根据勾股定理,得
∴ 0.3 + 0.5 = 0.8 (m).
∴ 水深的最大深度为 0.8 m.
同课章节目录
