5.8 三元一次方程组 课件(共23张PPT)-2023-2024学年八年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 5.8 三元一次方程组 课件(共23张PPT)-2023-2024学年八年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 804.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览





文档简介
北师大版 数学 八年级上册
第五章 二元一次方程组
?8 三元一次方程组
学习目标
1.理解三元一次方程(组)的定义,会判断一个方程组是不是三元一次方程组。
2.会用代入消元法和加减消元法解三元一次方程组,进一步体会消元思想.(重难点)
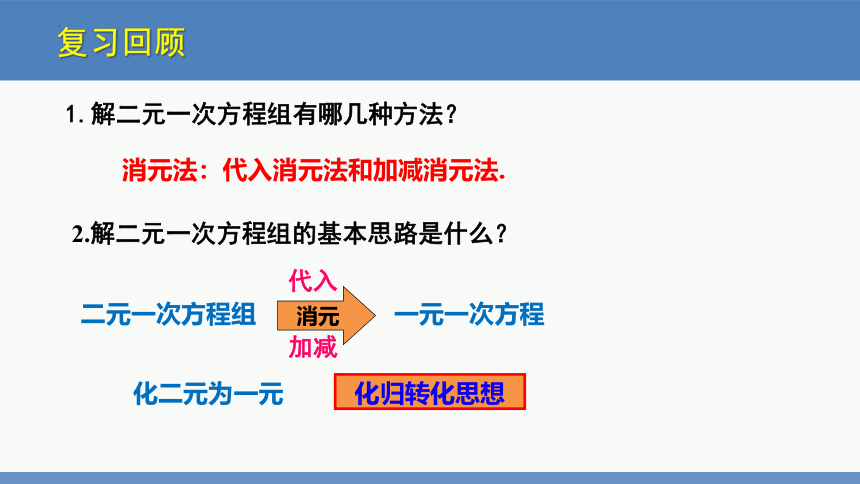
复习回顾
1.解二元一次方程组有哪几种方法?
2.解二元一次方程组的基本思路是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化二元为一元
化归转化思想
消元法:代入消元法和加减消元法.
③
一、创设情境,引入新知
问题:已知甲、乙、丙三数的和是23,甲数比乙数大1,甲数的2倍与乙数的和比丙数大20,求这三个数.
我们知道当问题中有两个未知数,两个等量关系时,可以列二元一次方程组解决.
但上述问题中有几个未知数,几个等量关系,该如何设未知数呢?
有三个未知数,三个等量关系,因此可以设三个未知数.
①
②
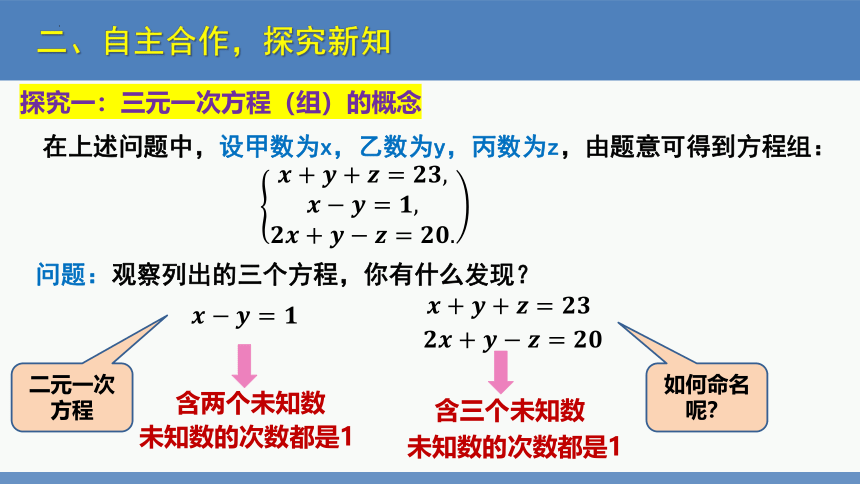
在上述问题中,设甲数为x,乙数为y,丙数为z,由题意可得到方程组:
二、自主合作,探究新知
探究一:三元一次方程(组)的概念
????+????+????=????????,?????????=????,????????+?????????=????????.
?
问题:观察列出的三个方程,你有什么发现?
未知数的次数都是1
含两个未知数
?????????=????
?
二元一次方程
如何命名呢?
未知数的次数都是1
含三个未知数
????+????+????=????????
?
????????+?????????=????????
?
二、自主合作,探究新知
像这样,共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
在这个方程组中,????+????+????=????????和????????+?????????=????????都含有三个未知数,并且所含未知数的项的次数都是1,这样的方程叫做三元一次方程.
?
知识要点
1.下列方程组中,是三元一次方程的是( )
A.????????+????=???? B.????+????????+????????=????
C.????????+????+????=???? D.????????????+?????????????=????
?
2.下列方程组中,是三元一次方程组的是( )
A.????+????+????=????????+????+????????=????????+????+????=???? B.????+????+????=????????+????????????=?????????????????????=????????
C. ????+????+????=?????????????+????=????????=????+???? D.????+????=????????+????????=????????+????=????
?
二、自主合作,探究新知
跟踪练习
D
C
二、自主合作,探究新知
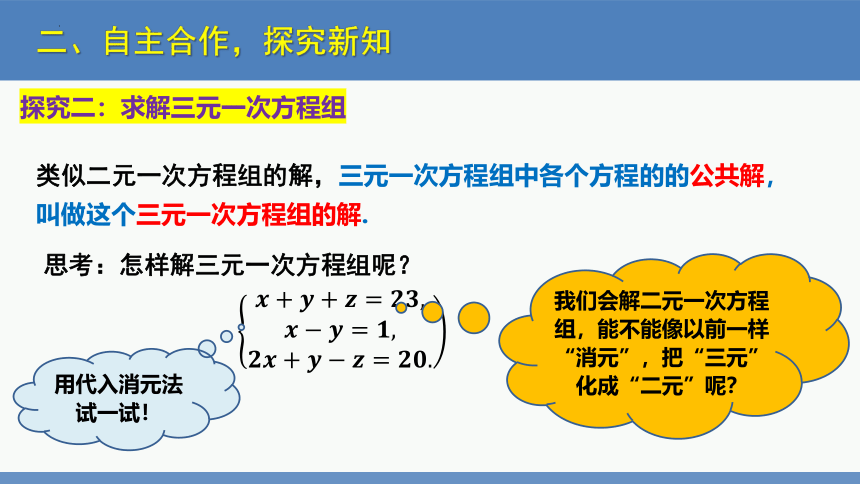
探究二:求解三元一次方程组
类似二元一次方程组的解,三元一次方程组中各个方程的的公共解,叫做这个三元一次方程组的解.
思考:怎样解三元一次方程组呢?
????+????+????=????????,?????????=????,????????+?????????=????????.
?
我们会解二元一次方程组,能不能像以前一样“消元”,把“三元”化成“二元”呢?
用代入消元法试一试!
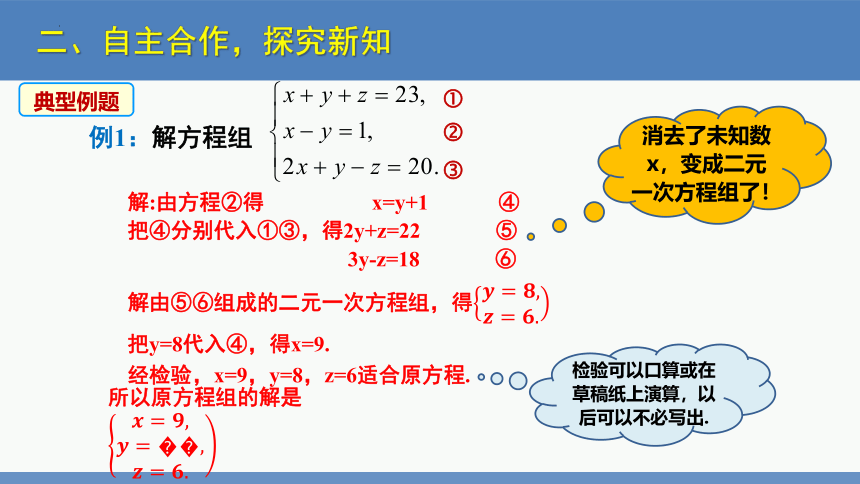
例1:解方程组
?
?
?
二、自主合作,探究新知
典型例题
解:由方程②得 x=y+1 ④
把④分别代入①③,得2y+z=22 ⑤
3y-z=18 ⑥
把y=8代入④,得x=9.
经检验,x=9,y=8,z=6适合原方程.
解由⑤⑥组成的二元一次方程组,得????=????,????=????.
?
所以原方程组的解是????=????,????=??,????=????.
?
消去了未知数x,变成二元一次方程组了!
检验可以口算或在草稿纸上演算,以后可以不必写出.
二、自主合作,探究新知
做一做
(1)解上面的方程组时,你能用代入消元法先消去未知数y(或z),从而得到方程组的解吗?
(2)你还有其他方法吗?与同伴进行交流.
解:(1)由方程②可变形为y=x-1 ,代入①和③中,可以先消去y.
议一议:上述不同的解法有什么共同之处?与二元一次方程组的解法有什么联系?解三元一次方程组的思路是什么?
(2)可以先利用加减消元,由方程①+③可消去z,得3x+2y=43
再与方程②联立即可求出x,y的值,进而求出z的值.
知识要点
二、自主合作,探究新知
解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
二、自主合作,探究新知
典型例题
例2:一个三位数,各位数字之和是14,个位数字、百位数字的和等于十位数字,百位数字的7倍比个位数字、十位数字的和大2,求这个三位数。
解:设个位数字是x,十位数字是y,百位数字是z.
解得
答:这个数是275.
2.三元一次方程组????+????=????????+????=????????+????=????的解是( )
A.????=????????=????????=???? B.????=????????=????????=???? C. ????=????????=????????=???? D.????=????????=????????=????
?
1.下列方程组中,是三元一次方程组的是( )
A.????????=????????????+????=????????+????+????=???? B.?????????????+????=??????????????????+????=????????=?????
C. ????+?????????=????????????????=?????????????????=???? D.????+????=????????+????=????????+????=????
?
三、即学即练,应用知识
D
A
4.解方程组?????????????+????=????,①????????+?????????????=????????,②????+????+????=????,③ 时,第一次消去未知数的最佳方法是( )
A.加减法消去x,①-③×2与②-③×2
B.加减法消去y,①+③与①×3+②
C.加减法消去z,①+②与③+②
D.代入法消去x,y,z中的任何一个
?
3.已知x,y,z满足方程组????+????=????,①????+????=????,②????+????=????,③ 则x+y+z的值为( )
A.4 B.5 C.8 D.10
?
三、即学即练,应用知识
A
C
三、即学即练,应用知识
5.小华到学校超市买铅笔11支,作业本5本,笔芯2支,共花12.5元;小刚在这家超市买同样的铅笔10 支,同样的作业本4本,同样的笔芯1支,共花10元.则买这样的铅笔1支、作业本1本、笔芯1支共需 元.
2.5
0
6.若????=????, ????=?????,????=????, 是三元一次方程?????????(?????????)????+????????=????的一组解,则m的值为 .
?
三、即学即练,应用知识
7.解方程组:????+?????????=?????, ①????+?????????=?????, ②????+?????????=????????, ③
?
解:由①+②,得 2y=-6,解得 y =-3,
②+③,得2x= 14,解得x=7,
把x=7,y=-3代入①,得-3+z-7=-5,解得z=5,
∴原方程组的解为????=????,????=?????,????=????.
?
四、课堂小结
三元一次方程组
含有三个未知数,并且所含未知数的项的次数都是1的方程叫做三元一次方程.
共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
三元一次方程(组)的概念
三元一次方程组中各个方程的的公共解,叫做这个三元一次方程组的解.
“消元法”——把“三元”化为“二元”,再化为“一元”.
三元一次方程组的解法
五、当堂达标检测
D
1.下列方程组中,是三元一次方程组的是( )
A.????=?????????????????????+????????+????????=?????????????????????=???? B.?????????????????=????????????+????????+????????=????????????+????=????
C. ????+????=????????+????=????????+????=???? D.????+????=????????+????=????????????+????=????????
?
2.解三元一次方程组?????????+????=?????,①????+?????????????=????,②????+????=????, ③ 要使解法较为简单,首先应进行的变形为( )
A.①+② B.①-② C.①+③ D.②-③
?
A
五、当堂达标检测
3.已知????=????,????=????,????=???? 是方程组????????+????????=????,????????+????????=????,????????+????????=????的解,则a+b+c的值是( )
A.3 B.2 C.1 D.无法确定
?
A
4.解方程组?????????????+????=????, ①????????+?????????????=????????,②????+?????????????=????, ③ 以下解法中不正确的是( )
A.由①,②消去z,再由①,③消去z
B.由①,③消去z,再由②,③消去z
C.由①,③消去y,再由①,②消去y
D.由①,②消去z,再由①,③消去y
?
D
五、当堂达标检测
5.解方程组:????+????+????=????????, ①????=????????? ,②????????+????=????+????????,③
?
?
五、当堂达标检测
解:由①+②+③,得 2x+2y+2z =90,即 x+y+z = 45 ④.
④-①,得z= 18;④-②,得x= 12;④-③,得y=15.
因此,原方程组的解为????=????????,????=????????,????=????????.
?
6.解方程组:????+????=????????, ①????+????=????????, ②????+????=????????, ③
?
五、当堂达标检测
7.某次运动会上,我国运动员顽强拼搏,获得金、银、铜牌共342枚.其中金牌枚数比银牌与铜牌枚数之和少40.铜牌枚数比金牌与银牌枚数之差多40,问金、银、铜牌各获得多少?
解:设获得金牌x枚,银牌y枚,铜牌z枚.
根据题意,得????+????+????=????????????,????+????????=????+????,?????????+????????=????,
解得????=????????????,????=????????????,????=????????.
答:获得金牌151枚,银牌108枚,铜牌83枚.
?
教材习题5.9;
六、布置作业
第五章 二元一次方程组
?8 三元一次方程组
学习目标
1.理解三元一次方程(组)的定义,会判断一个方程组是不是三元一次方程组。
2.会用代入消元法和加减消元法解三元一次方程组,进一步体会消元思想.(重难点)
复习回顾
1.解二元一次方程组有哪几种方法?
2.解二元一次方程组的基本思路是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化二元为一元
化归转化思想
消元法:代入消元法和加减消元法.
③
一、创设情境,引入新知
问题:已知甲、乙、丙三数的和是23,甲数比乙数大1,甲数的2倍与乙数的和比丙数大20,求这三个数.
我们知道当问题中有两个未知数,两个等量关系时,可以列二元一次方程组解决.
但上述问题中有几个未知数,几个等量关系,该如何设未知数呢?
有三个未知数,三个等量关系,因此可以设三个未知数.
①
②
在上述问题中,设甲数为x,乙数为y,丙数为z,由题意可得到方程组:
二、自主合作,探究新知
探究一:三元一次方程(组)的概念
????+????+????=????????,?????????=????,????????+?????????=????????.
?
问题:观察列出的三个方程,你有什么发现?
未知数的次数都是1
含两个未知数
?????????=????
?
二元一次方程
如何命名呢?
未知数的次数都是1
含三个未知数
????+????+????=????????
?
????????+?????????=????????
?
二、自主合作,探究新知
像这样,共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
在这个方程组中,????+????+????=????????和????????+?????????=????????都含有三个未知数,并且所含未知数的项的次数都是1,这样的方程叫做三元一次方程.
?
知识要点
1.下列方程组中,是三元一次方程的是( )
A.????????+????=???? B.????+????????+????????=????
C.????????+????+????=???? D.????????????+?????????????=????
?
2.下列方程组中,是三元一次方程组的是( )
A.????+????+????=????????+????+????????=????????+????+????=???? B.????+????+????=????????+????????????=?????????????????????=????????
C. ????+????+????=?????????????+????=????????=????+???? D.????+????=????????+????????=????????+????=????
?
二、自主合作,探究新知
跟踪练习
D
C
二、自主合作,探究新知
探究二:求解三元一次方程组
类似二元一次方程组的解,三元一次方程组中各个方程的的公共解,叫做这个三元一次方程组的解.
思考:怎样解三元一次方程组呢?
????+????+????=????????,?????????=????,????????+?????????=????????.
?
我们会解二元一次方程组,能不能像以前一样“消元”,把“三元”化成“二元”呢?
用代入消元法试一试!
例1:解方程组
?
?
?
二、自主合作,探究新知
典型例题
解:由方程②得 x=y+1 ④
把④分别代入①③,得2y+z=22 ⑤
3y-z=18 ⑥
把y=8代入④,得x=9.
经检验,x=9,y=8,z=6适合原方程.
解由⑤⑥组成的二元一次方程组,得????=????,????=????.
?
所以原方程组的解是????=????,????=??,????=????.
?
消去了未知数x,变成二元一次方程组了!
检验可以口算或在草稿纸上演算,以后可以不必写出.
二、自主合作,探究新知
做一做
(1)解上面的方程组时,你能用代入消元法先消去未知数y(或z),从而得到方程组的解吗?
(2)你还有其他方法吗?与同伴进行交流.
解:(1)由方程②可变形为y=x-1 ,代入①和③中,可以先消去y.
议一议:上述不同的解法有什么共同之处?与二元一次方程组的解法有什么联系?解三元一次方程组的思路是什么?
(2)可以先利用加减消元,由方程①+③可消去z,得3x+2y=43
再与方程②联立即可求出x,y的值,进而求出z的值.
知识要点
二、自主合作,探究新知
解三元一次方程组的基本思路是:通过“代入”或“加减”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
“三元”
“二元”
二元一次方程组
一元一次方程
二、自主合作,探究新知
典型例题
例2:一个三位数,各位数字之和是14,个位数字、百位数字的和等于十位数字,百位数字的7倍比个位数字、十位数字的和大2,求这个三位数。
解:设个位数字是x,十位数字是y,百位数字是z.
解得
答:这个数是275.
2.三元一次方程组????+????=????????+????=????????+????=????的解是( )
A.????=????????=????????=???? B.????=????????=????????=???? C. ????=????????=????????=???? D.????=????????=????????=????
?
1.下列方程组中,是三元一次方程组的是( )
A.????????=????????????+????=????????+????+????=???? B.?????????????+????=??????????????????+????=????????=?????
C. ????+?????????=????????????????=?????????????????=???? D.????+????=????????+????=????????+????=????
?
三、即学即练,应用知识
D
A
4.解方程组?????????????+????=????,①????????+?????????????=????????,②????+????+????=????,③ 时,第一次消去未知数的最佳方法是( )
A.加减法消去x,①-③×2与②-③×2
B.加减法消去y,①+③与①×3+②
C.加减法消去z,①+②与③+②
D.代入法消去x,y,z中的任何一个
?
3.已知x,y,z满足方程组????+????=????,①????+????=????,②????+????=????,③ 则x+y+z的值为( )
A.4 B.5 C.8 D.10
?
三、即学即练,应用知识
A
C
三、即学即练,应用知识
5.小华到学校超市买铅笔11支,作业本5本,笔芯2支,共花12.5元;小刚在这家超市买同样的铅笔10 支,同样的作业本4本,同样的笔芯1支,共花10元.则买这样的铅笔1支、作业本1本、笔芯1支共需 元.
2.5
0
6.若????=????, ????=?????,????=????, 是三元一次方程?????????(?????????)????+????????=????的一组解,则m的值为 .
?
三、即学即练,应用知识
7.解方程组:????+?????????=?????, ①????+?????????=?????, ②????+?????????=????????, ③
?
解:由①+②,得 2y=-6,解得 y =-3,
②+③,得2x= 14,解得x=7,
把x=7,y=-3代入①,得-3+z-7=-5,解得z=5,
∴原方程组的解为????=????,????=?????,????=????.
?
四、课堂小结
三元一次方程组
含有三个未知数,并且所含未知数的项的次数都是1的方程叫做三元一次方程.
共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
三元一次方程(组)的概念
三元一次方程组中各个方程的的公共解,叫做这个三元一次方程组的解.
“消元法”——把“三元”化为“二元”,再化为“一元”.
三元一次方程组的解法
五、当堂达标检测
D
1.下列方程组中,是三元一次方程组的是( )
A.????=?????????????????????+????????+????????=?????????????????????=???? B.?????????????????=????????????+????????+????????=????????????+????=????
C. ????+????=????????+????=????????+????=???? D.????+????=????????+????=????????????+????=????????
?
2.解三元一次方程组?????????+????=?????,①????+?????????????=????,②????+????=????, ③ 要使解法较为简单,首先应进行的变形为( )
A.①+② B.①-② C.①+③ D.②-③
?
A
五、当堂达标检测
3.已知????=????,????=????,????=???? 是方程组????????+????????=????,????????+????????=????,????????+????????=????的解,则a+b+c的值是( )
A.3 B.2 C.1 D.无法确定
?
A
4.解方程组?????????????+????=????, ①????????+?????????????=????????,②????+?????????????=????, ③ 以下解法中不正确的是( )
A.由①,②消去z,再由①,③消去z
B.由①,③消去z,再由②,③消去z
C.由①,③消去y,再由①,②消去y
D.由①,②消去z,再由①,③消去y
?
D
五、当堂达标检测
5.解方程组:????+????+????=????????, ①????=????????? ,②????????+????=????+????????,③
?
?
五、当堂达标检测
解:由①+②+③,得 2x+2y+2z =90,即 x+y+z = 45 ④.
④-①,得z= 18;④-②,得x= 12;④-③,得y=15.
因此,原方程组的解为????=????????,????=????????,????=????????.
?
6.解方程组:????+????=????????, ①????+????=????????, ②????+????=????????, ③
?
五、当堂达标检测
7.某次运动会上,我国运动员顽强拼搏,获得金、银、铜牌共342枚.其中金牌枚数比银牌与铜牌枚数之和少40.铜牌枚数比金牌与银牌枚数之差多40,问金、银、铜牌各获得多少?
解:设获得金牌x枚,银牌y枚,铜牌z枚.
根据题意,得????+????+????=????????????,????+????????=????+????,?????????+????????=????,
解得????=????????????,????=????????????,????=????????.
答:获得金牌151枚,银牌108枚,铜牌83枚.
?
教材习题5.9;
六、布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
