10.4 分式的加减 课件(共27张PPT)-2023-2024学年七年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 10.4 分式的加减 课件(共27张PPT)-2023-2024学年七年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览





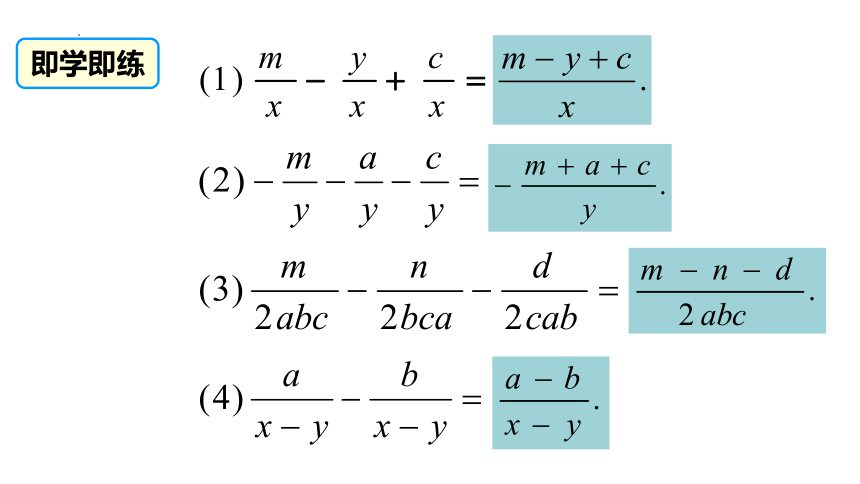


文档简介
(共27张PPT)
第九章 整式
第2节 分式的运算
10.4 分式的加减
1.理解并掌握分式的加减法法则,体会类比思想.
2.运用法则进行分式的加减运算,体会化归思想.
思考
1.同分母分数相加减, 不变, 相加减;异分母分数相加减,先 ,变为 ,
再 .
分母
分子
通分
同分母分数
加减
同分母分数的加减法则是否可以推广到同分母分式的加减呢
如何计算
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减.
上述法则可用式子表示为
即学即练
解:(1)
=
=
例题1 计算:
教材第78页
解:(2)
=
=
=
解:
=
=
注意:结果要化为最简分式!
=
例题1
=
教材第78页
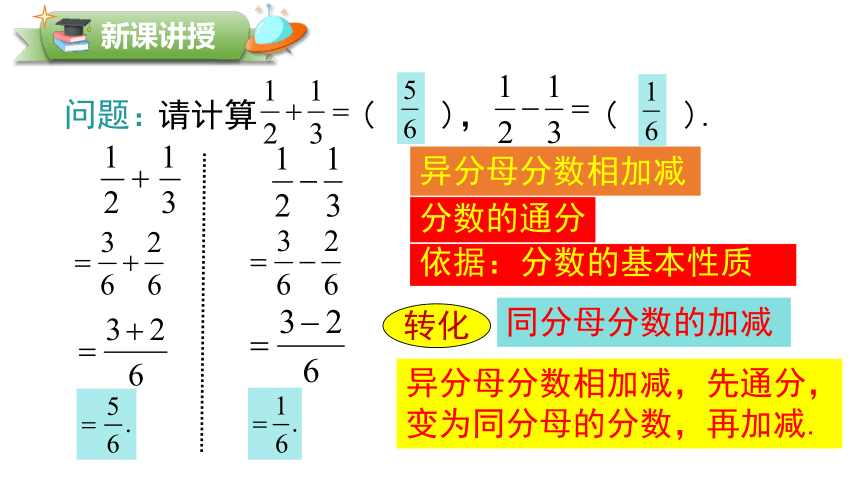
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
异分母分式的加减法则
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
知识总结
最小公倍数:24
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分数的值.
通分的关键是确定几个分母的最小公倍数
问题1:通分: 与
解:
分式的通分
想一想:
联想分数的通分,由上述两个问题你能想出如何将分式进行通分吗?
(b≠0).
问题2:填空:
通分的定义
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
通分先要确定公分母,如果各分母的系数是整数,通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母.这样的公分母叫做最简公分母
例题2 将分式 化成分母分别为下列整式的分式:
(1)2x; (2)xy;
(3)x2y2; (4)x(x+2).
解:(1)
=
教材第80页
例题2 将分式 化成分母分别为下列整式的分式:
(1)2x; (2)xy;
(3)x2y2; (4)x(x+2).
教材第80页
解:原式 =
=
例题3 计算:
解:原式 =
=
教材第81页
=
例题3 计算:
解:原式 =
=
解:原式 =
=
教材第81页
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
知识总结
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
例题4 计算:
x
A
D
D
B
6.如图的解题过程中,第①步出现错误,但最后所求的值是正确的,则图中被污染的x的值是________.
5
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
第九章 整式
第2节 分式的运算
10.4 分式的加减
1.理解并掌握分式的加减法法则,体会类比思想.
2.运用法则进行分式的加减运算,体会化归思想.
思考
1.同分母分数相加减, 不变, 相加减;异分母分数相加减,先 ,变为 ,
再 .
分母
分子
通分
同分母分数
加减
同分母分数的加减法则是否可以推广到同分母分式的加减呢
如何计算
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减.
上述法则可用式子表示为
即学即练
解:(1)
=
=
例题1 计算:
教材第78页
解:(2)
=
=
=
解:
=
=
注意:结果要化为最简分式!
=
例题1
=
教材第78页
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
异分母分式的加减法则
异分母分式相加减,先通分,变为同分母的分式,再加减.
上述法则可用式子表示为
知识总结
最小公倍数:24
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分数的值.
通分的关键是确定几个分母的最小公倍数
问题1:通分: 与
解:
分式的通分
想一想:
联想分数的通分,由上述两个问题你能想出如何将分式进行通分吗?
(b≠0).
问题2:填空:
通分的定义
根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.
通分先要确定公分母,如果各分母的系数是整数,通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母.这样的公分母叫做最简公分母
例题2 将分式 化成分母分别为下列整式的分式:
(1)2x; (2)xy;
(3)x2y2; (4)x(x+2).
解:(1)
=
教材第80页
例题2 将分式 化成分母分别为下列整式的分式:
(1)2x; (2)xy;
(3)x2y2; (4)x(x+2).
教材第80页
解:原式 =
=
例题3 计算:
解:原式 =
=
教材第81页
=
例题3 计算:
解:原式 =
=
解:原式 =
=
教材第81页
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
知识总结
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
例题4 计算:
x
A
D
D
B
6.如图的解题过程中,第①步出现错误,但最后所求的值是正确的,则图中被污染的x的值是________.
5
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
