代入消元法
图片预览






文档简介
课件14张PPT。8.2 消 元(1)
————代入消元法 团风县实验中学 王红艳 主讲创设问题情境,导入新课 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.如果某队为了争取较好名次,想在全部22场比赛中得40分,那么这个队胜负场数应分别是多少?你会用一元一次方程来解答这个问题吗?以上的方程组与方程有什么联系?解:设胜x场,负y场;③是一元一次方程,求解当然容易了!解:设胜x场;则有:2x+(22-x)=40由①我们可以得到:y=22-x
再将②中的y换为22-x,就得到了③由上面的方法求出方程组的解,你有何体会? 二元一次方程组中有两个未知数,如果消去其中的一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程。我们就可以先解出一个未知数,然后就可以很简单的求出另一个未知数。这种将未知数的个数有多化少、逐一解决的想法叫做消元思想。2x+(22-x)=40解:由① ,得 y=22-x ③
将③代入② ,得 2x+(22-x)=40
x=18
将x=18代入③,得 y=4
解:将①代入② ,得 3(y+5)-8y=20
3y+15-8y=20
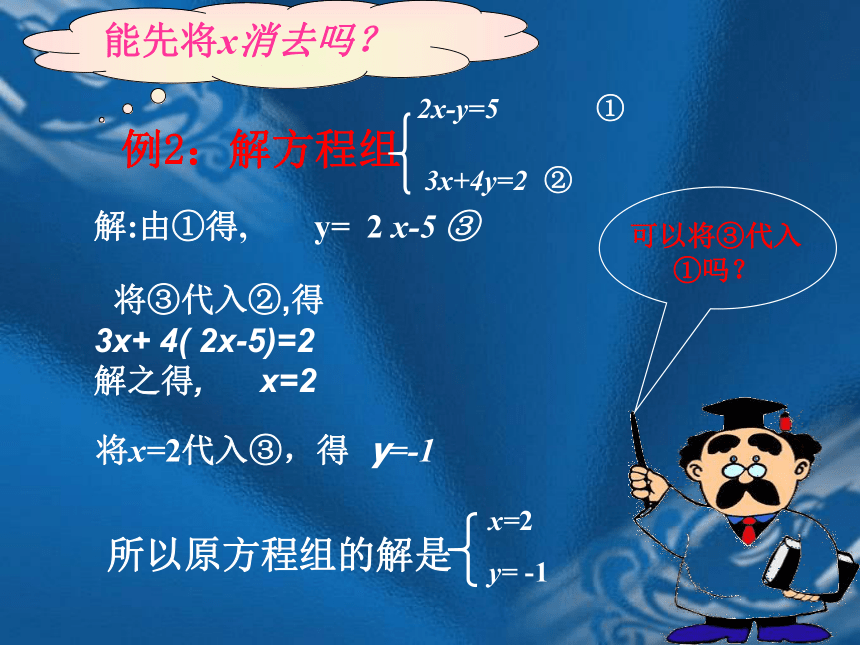
y=-1在实践中学习把y=-1代入②可以吗?能先将x消去吗?解:由①得, y= 2 x-5 ③ 将x=2代入③,得 y=-1可以将③代入①吗?将③代入②,得3x+ 4( 2x-5)=2
解之得, x=2
解法2:由①得,x=(5+y)/2 ③ , 将③代入②,
3(5+y)/2+4y=2
y=-1哪种方法更简单? 小结:所以在解题过程中,通常将其中一个未知数较简单(最好是1或-1)的方程作适当变形,写成用一个未知数表示另一个未知数的形式,再代入另一个方程中,如上例中,方程①中y的系数是-1,用含x式子表示y,比较简便。
将y=-1代入③,得 x= 2将③代入② ,得 2x-(21-3x)=-11 x=2 解:由①,得 5y=21-3x ③ 把求出的解代入原方程组,可以知道你解得对不对。 例3:解方程组代入①,消去 了!把②变形得:标准的代入消元法还有没有更简便的方法?将x=2代入③中,得y=3简便的整体代入消元法(A)由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2)。(B)由①,得 ③,把③代入②,得 。(C)由②,得 ③,把③代入①,得 。(D)把②代入 ①,得11-2y-y=2,把(3x看作一个整体)D细心选一选1、已知方程3x+y=5,用含x的代数式表示y,则得 ,用含y的代数式表示x,则得———— 。
2、用代入法解方程组{3x+4y=5 ① 较简便的解
法步骤是:先把方程———— 变形为 ——————,再代入方程————,求得———的值,然后再求———的值。
3、已知2x+3y=-5,则3(3y+2x)-2(x+y)-y的值————————(考虑整体代入)耐心填一填2y-3x=0②y=5-3xx=(5-y) /3②3x=2y①yx解:3(3y+2x)-2(x+y)-y =9y+6x-2x-2y-y
=4x+6y =2(2x+3y)=-10
今天通过学习你体会到解二元一次方程的基本思路是什么?有哪些步骤?代入消元法的步骤②将y=ax+b代入方程组中的另一个方程中,消去y,得到关于二的一元一次方程; ③解这个一元一次方程,求出x的值; ④把求得的x值代入方程y=ax+b中,求出y的值,再写出方程组解的形式;⑤检验得到的解是不是原方程组的解.这一步不是完全必要的,若能肯定解题无误,这一点可以省略。 1、解二元一次方程组-310/3感悟数学,
娱乐生活!
————代入消元法 团风县实验中学 王红艳 主讲创设问题情境,导入新课 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.如果某队为了争取较好名次,想在全部22场比赛中得40分,那么这个队胜负场数应分别是多少?你会用一元一次方程来解答这个问题吗?以上的方程组与方程有什么联系?解:设胜x场,负y场;③是一元一次方程,求解当然容易了!解:设胜x场;则有:2x+(22-x)=40由①我们可以得到:y=22-x
再将②中的y换为22-x,就得到了③由上面的方法求出方程组的解,你有何体会? 二元一次方程组中有两个未知数,如果消去其中的一个未知数,将二元一次方程组转化为我们熟悉的一元一次方程。我们就可以先解出一个未知数,然后就可以很简单的求出另一个未知数。这种将未知数的个数有多化少、逐一解决的想法叫做消元思想。2x+(22-x)=40解:由① ,得 y=22-x ③
将③代入② ,得 2x+(22-x)=40
x=18
将x=18代入③,得 y=4
解:将①代入② ,得 3(y+5)-8y=20
3y+15-8y=20
y=-1在实践中学习把y=-1代入②可以吗?能先将x消去吗?解:由①得, y= 2 x-5 ③ 将x=2代入③,得 y=-1可以将③代入①吗?将③代入②,得3x+ 4( 2x-5)=2
解之得, x=2
解法2:由①得,x=(5+y)/2 ③ , 将③代入②,
3(5+y)/2+4y=2
y=-1哪种方法更简单? 小结:所以在解题过程中,通常将其中一个未知数较简单(最好是1或-1)的方程作适当变形,写成用一个未知数表示另一个未知数的形式,再代入另一个方程中,如上例中,方程①中y的系数是-1,用含x式子表示y,比较简便。
将y=-1代入③,得 x= 2将③代入② ,得 2x-(21-3x)=-11 x=2 解:由①,得 5y=21-3x ③ 把求出的解代入原方程组,可以知道你解得对不对。 例3:解方程组代入①,消去 了!把②变形得:标准的代入消元法还有没有更简便的方法?将x=2代入③中,得y=3简便的整体代入消元法(A)由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2)。(B)由①,得 ③,把③代入②,得 。(C)由②,得 ③,把③代入①,得 。(D)把②代入 ①,得11-2y-y=2,把(3x看作一个整体)D细心选一选1、已知方程3x+y=5,用含x的代数式表示y,则得 ,用含y的代数式表示x,则得———— 。
2、用代入法解方程组{3x+4y=5 ① 较简便的解
法步骤是:先把方程———— 变形为 ——————,再代入方程————,求得———的值,然后再求———的值。
3、已知2x+3y=-5,则3(3y+2x)-2(x+y)-y的值————————(考虑整体代入)耐心填一填2y-3x=0②y=5-3xx=(5-y) /3②3x=2y①yx解:3(3y+2x)-2(x+y)-y =9y+6x-2x-2y-y
=4x+6y =2(2x+3y)=-10
今天通过学习你体会到解二元一次方程的基本思路是什么?有哪些步骤?代入消元法的步骤②将y=ax+b代入方程组中的另一个方程中,消去y,得到关于二的一元一次方程; ③解这个一元一次方程,求出x的值; ④把求得的x值代入方程y=ax+b中,求出y的值,再写出方程组解的形式;⑤检验得到的解是不是原方程组的解.这一步不是完全必要的,若能肯定解题无误,这一点可以省略。 1、解二元一次方程组-310/3感悟数学,
娱乐生活!
