2023-2024学年人教版九年级数学上册第24章 圆 单元综合训练(无答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册第24章 圆 单元综合训练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 18:25:44 | ||
图片预览


文档简介
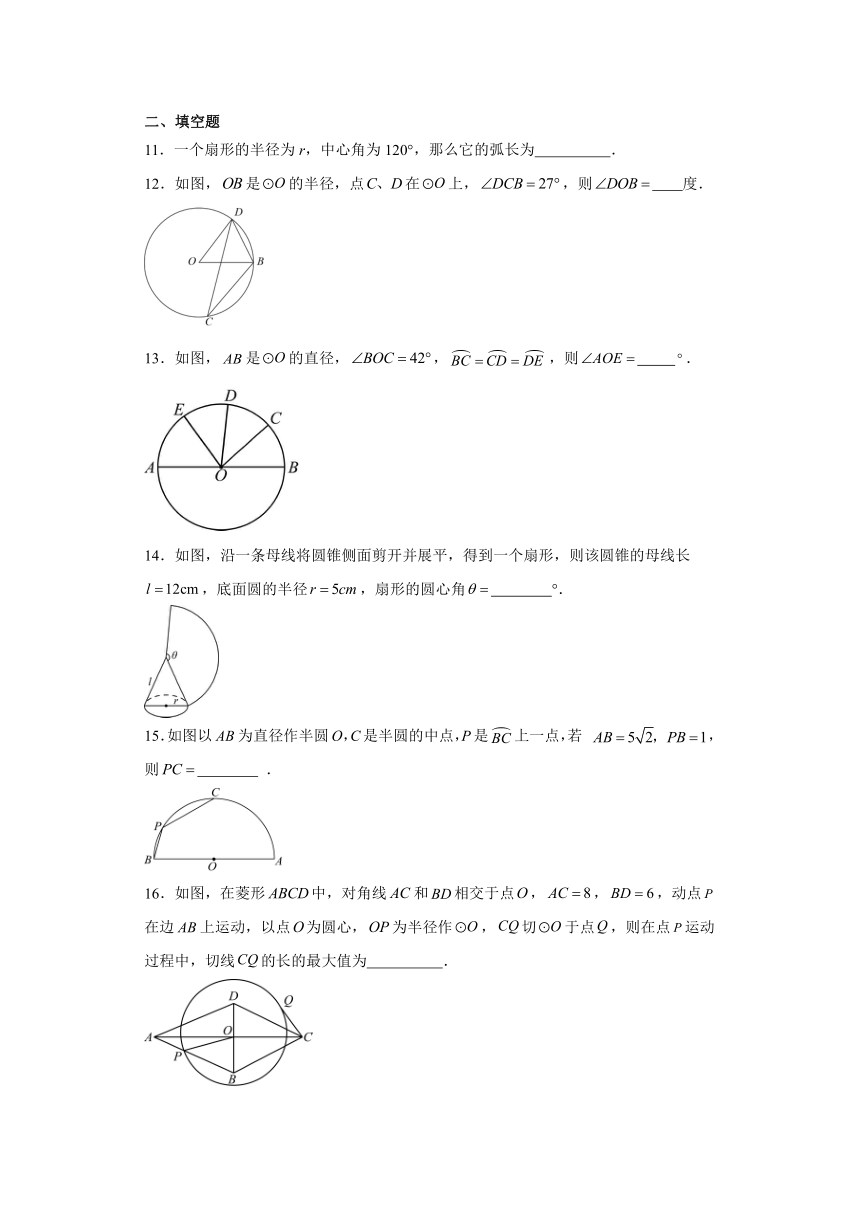
第24章 圆 单元综合训练
一、单选题
1.下列结论不正确的是( )
A.圆心也是圆的一部分 B.一个圆中最长的弦是直径
C.圆是轴对称图形 D.等弧所在的圆一定是等圆或同圆
2.平面内有两点、,的半径为5,若,则点与的位置关系是( )
A.点在外 B.点在上 C.点在内 D.无法判断
3.已知的半径是,圆心O到直线l的距离是,则直线l与的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
4.利用圆的等分,在半径为3的圆中作出如图的图案,则相邻两等分点之间的距离为( )
A.3 B. C.4 D.6
5.下列说法正确的是( )
A.平分弦的直径垂直于弦 B.圆的切线垂直于圆的半径
C.三角形的外心到三角形三边的距离相等 D.同弧或等弧所对的圆周角相等
6.如图,为的直径,弦于点,已知,则的长为( )
A.16 B.12 C.10 D.8
7.如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线与相交于C,D两点,若,则的长为( )
A. B.4 C. D.
8.如图,在半径为4的中,将劣弧沿弦翻折,折叠后的恰好与,相切,则阴影部分的面积为( )
A. B. C. D.
9.如图,是的直径,内接于,延长在外相交于点,若,则的度数是( )
A. B. C. D.
10.如图,点A是上一定点,点B是上一动点、连接、、、分别将线段、绕点A顺时针旋转到,,连接,,,,下列结论正确的有( )
①点在上;②;③;④当时,与相切.
A.4个 B.3个 C.2个 D.1个
二、填空题
11.一个扇形的半径为r,中心角为120°,那么它的弧长为 .
12.如图,是的半径,点在上,,则 度.
13.如图,是的直径,,,则 .
14.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,则该圆锥的母线长,底面圆的半径,扇形的圆心角 °.
15.如图以为直径作半圆O,C是半圆的中点,P是上一点,若 ,则 .
16.如图,在菱形中,对角线和相交于点,,,动点在边上运动,以点为圆心,为半径作,切于点,则在点运动过程中,切线的长的最大值为 .
三、解答题
17.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.
求证:OD=CD.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,CD=6,求AE的长.
19.如图,AB是的直径,C为半圆O上一点,直线l经过点C,过点A作于点D,连接AC,当AC平分时,求证:直线l是的切线.
20.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=35°.
(1)求∠AOB的度数;
(2)若OE=6,求扇形EOF的面积.
21.在⊙O中,弦与直径相交于点P.
若,,则= ;= ;
若的度数为m度、的度数为n度,猜想:∠APD的度数与m、n之间的数量关系,并证明你的结论
22.如图,AB是的直径,弦AD平分,过点D的切线交AC于点E.
(1)DE与AC有怎样的位置关系?为什么?
(2)若,,求线段DE的长度.
23.如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过P点作FP⊥PE交AC于F点,经过P、E、F三点确定⊙O.
(1)试说明:点C也一定在⊙O上.
(2)点E在运动过程中,∠PFE的度数是否变化?若不变,求出∠PFE的度数;若变化,说明理由.
(3)求线段EF的取值范围,并说明理由.
24.如图,内接于,弦、相交于点,.
(1)如图1,求证:为的直径;
(2)如图2,过点作,求证:;
(3)如图3,在(2)的条件下,与相交于点,连接并延长交于点,连接,沿所在直线作劣弧的轴对称图形经过点,,,求线段的长度.
一、单选题
1.下列结论不正确的是( )
A.圆心也是圆的一部分 B.一个圆中最长的弦是直径
C.圆是轴对称图形 D.等弧所在的圆一定是等圆或同圆
2.平面内有两点、,的半径为5,若,则点与的位置关系是( )
A.点在外 B.点在上 C.点在内 D.无法判断
3.已知的半径是,圆心O到直线l的距离是,则直线l与的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
4.利用圆的等分,在半径为3的圆中作出如图的图案,则相邻两等分点之间的距离为( )
A.3 B. C.4 D.6
5.下列说法正确的是( )
A.平分弦的直径垂直于弦 B.圆的切线垂直于圆的半径
C.三角形的外心到三角形三边的距离相等 D.同弧或等弧所对的圆周角相等
6.如图,为的直径,弦于点,已知,则的长为( )
A.16 B.12 C.10 D.8
7.如图,是的直径,分别以点O和点B为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线与相交于C,D两点,若,则的长为( )
A. B.4 C. D.
8.如图,在半径为4的中,将劣弧沿弦翻折,折叠后的恰好与,相切,则阴影部分的面积为( )
A. B. C. D.
9.如图,是的直径,内接于,延长在外相交于点,若,则的度数是( )
A. B. C. D.
10.如图,点A是上一定点,点B是上一动点、连接、、、分别将线段、绕点A顺时针旋转到,,连接,,,,下列结论正确的有( )
①点在上;②;③;④当时,与相切.
A.4个 B.3个 C.2个 D.1个
二、填空题
11.一个扇形的半径为r,中心角为120°,那么它的弧长为 .
12.如图,是的半径,点在上,,则 度.
13.如图,是的直径,,,则 .
14.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,则该圆锥的母线长,底面圆的半径,扇形的圆心角 °.
15.如图以为直径作半圆O,C是半圆的中点,P是上一点,若 ,则 .
16.如图,在菱形中,对角线和相交于点,,,动点在边上运动,以点为圆心,为半径作,切于点,则在点运动过程中,切线的长的最大值为 .
三、解答题
17.如图,点O是△ABC的内心,AO的延长线和△ABC的外接圆相交于点D,连结CD.
求证:OD=CD.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,CD=6,求AE的长.
19.如图,AB是的直径,C为半圆O上一点,直线l经过点C,过点A作于点D,连接AC,当AC平分时,求证:直线l是的切线.
20.如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=35°.
(1)求∠AOB的度数;
(2)若OE=6,求扇形EOF的面积.
21.在⊙O中,弦与直径相交于点P.
若,,则= ;= ;
若的度数为m度、的度数为n度,猜想:∠APD的度数与m、n之间的数量关系,并证明你的结论
22.如图,AB是的直径,弦AD平分,过点D的切线交AC于点E.
(1)DE与AC有怎样的位置关系?为什么?
(2)若,,求线段DE的长度.
23.如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过P点作FP⊥PE交AC于F点,经过P、E、F三点确定⊙O.
(1)试说明:点C也一定在⊙O上.
(2)点E在运动过程中,∠PFE的度数是否变化?若不变,求出∠PFE的度数;若变化,说明理由.
(3)求线段EF的取值范围,并说明理由.
24.如图,内接于,弦、相交于点,.
(1)如图1,求证:为的直径;
(2)如图2,过点作,求证:;
(3)如图3,在(2)的条件下,与相交于点,连接并延长交于点,连接,沿所在直线作劣弧的轴对称图形经过点,,,求线段的长度.
同课章节目录
