24.1圆的有关性质 同步练习 (含答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1圆的有关性质 同步练习 (含答案)2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 18:44:22 | ||
图片预览


文档简介
24.1圆的有关性质 同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.90° D.100°
2.如图,点、、在上,若,则的度数是( )
A.18° B.36° C.54° D.72°
3.如图,BD是⊙O的直径,点A,C在⊙O上,=,∠_AOB= 60°,则∠BDC的度数是( )
A.60° B.45° C.35° D.30°
4.如图,的半径为6,半径于点D,,则的长是( )
A.3 B.2 C. D.
5.如图,C,D是以线段AB为直径的⊙O上两点(位于AB两侧),CD=AD,且∠ABC=70°,则∠BAD的度数是( )
A.50° B.45° C.35° D.30°
6.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B D.无法确定
7.如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是( )
A.30≤x≤60 B.30≤x≤90 C.30≤x≤120 D.60≤x≤120
8.如图所示,半径为5的中,弦BC,ED所对的圆心角分別是,.已知,则弦BC的弦心距等于( ).
A.4 B.3 C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是
10.
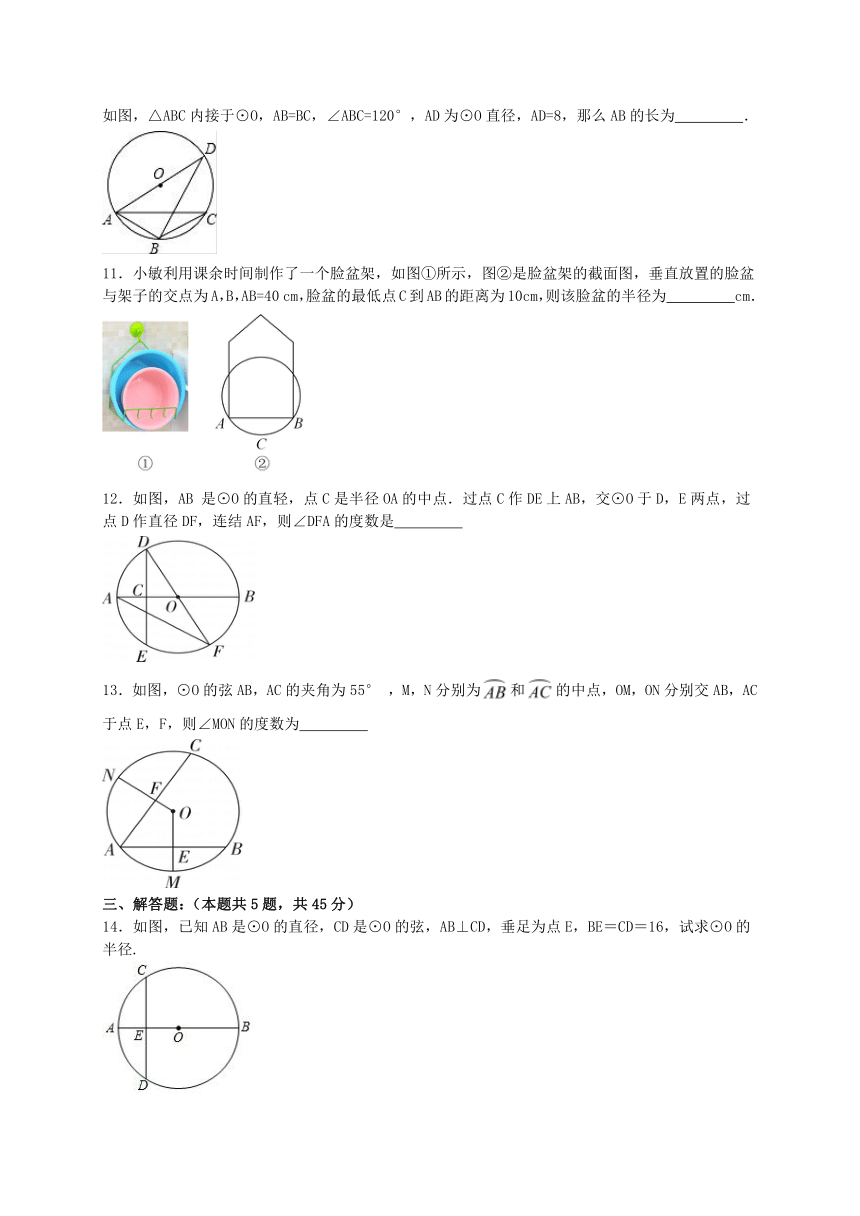
如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O直径,AD=8,那么AB的长为 .
11.小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
12.如图,AB 是⊙O的直轻,点C是半径OA的中点.过点C作DE上AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA的度数是
13.如图,⊙O的弦AB,AC的夹角为55° ,M,N分别为和的中点,OM,ON分别交AB,AC于点E,F,则∠MON的度数为
三、解答题:(本题共5题,共45分)
14.如图,已知AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,BE=CD=16,试求⊙O的半径.
15.如图所示,CD是的直径,OE是的半径,交于点,且,求的度数.
16.已知:如图,在△ABC中,AB为⊙O的直径,BC,AC分别交⊙O于D、E两点,若 ,求证:AB=AC
17.如图,是的直径,弦于点E,点P在上,.
(1)求证:;
(2)若,求的半径.
18.如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB不符合题意的关系式.
参考答案:
1.D 2.B 3.D 4.A 5.C 6.C 7.A 8.B
9.120°
10.4
11.25
12.30°
13.125°
14.解:连接OD,
设OB=OD=R,则OE=16﹣R,
∵直径AB⊥CD,CD=16,
∴∠OED=90°,DE= CD=8,
由勾股定理得:OD2=OE2+DE2
则R2=(16﹣R)2+82
解得:R=10,
∴⊙O的半径为10.
15.解:连结OB,
∵AB=OC,OB=OC,
∴AB=OB,
∴∠A=∠BOC,
∵OB=OE,
∴∠OBE=∠E,
又∵∠OBE=∠A+∠BOC=2∠A,
∴∠E=2∠A,
∴∠EOD=∠E+∠A=3∠A=84°,
∴∠A=28°.
16.证明:连接AD ∵AB为圆O的直径, ∴∠ADB=∠ADC=90°,∵ , ∴∠BAD=∠CAD, ∵在△ABD和△ACD中, ,∴△ABD≌△ACD(ASA). ∴AB=AC
17.(1)证明:∵,,
∴,
∴;
(2)解:连接,
设,则,
∵弦于点E,,
∴,
∵,
∴,
在中:,
∴,
解得:,
∴的半径为5.
18.(1)解:如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE
(2)解:BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF
(3)解:小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
∴△BAC≌△GAC(ASA),
∴AG=AB= BG,
∴CF=2AB
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.90° D.100°
2.如图,点、、在上,若,则的度数是( )
A.18° B.36° C.54° D.72°
3.如图,BD是⊙O的直径,点A,C在⊙O上,=,∠_AOB= 60°,则∠BDC的度数是( )
A.60° B.45° C.35° D.30°
4.如图,的半径为6,半径于点D,,则的长是( )
A.3 B.2 C. D.
5.如图,C,D是以线段AB为直径的⊙O上两点(位于AB两侧),CD=AD,且∠ABC=70°,则∠BAD的度数是( )
A.50° B.45° C.35° D.30°
6.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B D.无法确定
7.如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是( )
A.30≤x≤60 B.30≤x≤90 C.30≤x≤120 D.60≤x≤120
8.如图所示,半径为5的中,弦BC,ED所对的圆心角分別是,.已知,则弦BC的弦心距等于( ).
A.4 B.3 C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4:3:5,则∠D的度数是
10.
如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O直径,AD=8,那么AB的长为 .
11.小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
12.如图,AB 是⊙O的直轻,点C是半径OA的中点.过点C作DE上AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA的度数是
13.如图,⊙O的弦AB,AC的夹角为55° ,M,N分别为和的中点,OM,ON分别交AB,AC于点E,F,则∠MON的度数为
三、解答题:(本题共5题,共45分)
14.如图,已知AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,BE=CD=16,试求⊙O的半径.
15.如图所示,CD是的直径,OE是的半径,交于点,且,求的度数.
16.已知:如图,在△ABC中,AB为⊙O的直径,BC,AC分别交⊙O于D、E两点,若 ,求证:AB=AC
17.如图,是的直径,弦于点E,点P在上,.
(1)求证:;
(2)若,求的半径.
18.如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB不符合题意的关系式.
参考答案:
1.D 2.B 3.D 4.A 5.C 6.C 7.A 8.B
9.120°
10.4
11.25
12.30°
13.125°
14.解:连接OD,
设OB=OD=R,则OE=16﹣R,
∵直径AB⊥CD,CD=16,
∴∠OED=90°,DE= CD=8,
由勾股定理得:OD2=OE2+DE2
则R2=(16﹣R)2+82
解得:R=10,
∴⊙O的半径为10.
15.解:连结OB,
∵AB=OC,OB=OC,
∴AB=OB,
∴∠A=∠BOC,
∵OB=OE,
∴∠OBE=∠E,
又∵∠OBE=∠A+∠BOC=2∠A,
∴∠E=2∠A,
∴∠EOD=∠E+∠A=3∠A=84°,
∴∠A=28°.
16.证明:连接AD ∵AB为圆O的直径, ∴∠ADB=∠ADC=90°,∵ , ∴∠BAD=∠CAD, ∵在△ABD和△ACD中, ,∴△ABD≌△ACD(ASA). ∴AB=AC
17.(1)证明:∵,,
∴,
∴;
(2)解:连接,
设,则,
∵弦于点E,,
∴,
∵,
∴,
在中:,
∴,
解得:,
∴的半径为5.
18.(1)解:如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE
(2)解:BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF
(3)解:小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
∴△BAC≌△GAC(ASA),
∴AG=AB= BG,
∴CF=2AB
同课章节目录
