新人教A版必修第一册 第五章 三角函数 单元测试(含解析)
文档属性
| 名称 | 新人教A版必修第一册 第五章 三角函数 单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 818.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 11:20:21 | ||
图片预览




文档简介
第五章 三角函数 单元测试
学校:___________姓名:___________班级:___________考号:___________
一、单选择:共40分.只有一项是符合题目要求的.
1.已知函数,点是曲线相邻的两个对称中心,点是的一个最值点,若的面积为1,则( )
A.1 B. C.2 D.
2.下列命题中正确的是( )
A.如果我们把相等的角视为同一个角,则弧度制建立了一个从任意角的集合到实数集的一一对应的关系
B.弧度制表示角时,不同大小的弧度可以表示同一个角
C.终边相同的角的弧度制表示相差
D.终边相同的角的弧度都相同
3.工艺扇面是中国书面一种常见的表现形式.某同学想用布料制作一面如图所示的扇面.已知扇面展开的中心角为,外圆半径为20cm,内圆半径为10cm.则制作这样一面扇面需要的布料为( )cm
A. B. C. D.
4.若,,则角的终边在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知,,,若,则( )
A. B. C. D.
6.要得到函数的图象,只需将函数的图象上所有的点( )
A.再向左平行移动个单位长度 B.再向右平行移动个单位长度
C.再向右平行移动个单位长度 D.再向左平行移动个单位长度
7.已知函数是偶函数,其中,则下列关于函数描述正确的是
A.在区间上的最小值为-1
B.的图象可由函数的图象先向上平移2个单位,再向右平移个单位得到
C.的图象可由函数的图象向左平方移个单位得到
D.的图象可由函数的图象向右平方移个单位得到
8.已知,则( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.如图是函数的部分图象,则下列选项正确的是( )
A. B.
C. D.
10.已知函数,则( )
A.最小正周期为 B.关于直线对称
C.在上单调递减 D.最大值为
11.已知,则( )
A. B.
C. D.
12.定义为a,b中较大的数,已知函数,给出下列命题:其中正确的为( )
A.为非奇非偶函数;
B.是以为最小正周期的周期函数;
C.的值域为;
D.当时,.
三、填空题(20分)
13.若,则 .
14.已知是定义在(0,3)上的函数,的图象如图所示,则不等式的解集是 .
15.已知,,则 .
16.已知函数,则不等式在上的解集为 .
四、解答题(70分)
17.在这春光明媚的季节里,2021江苏省梁丰高级中学“校长杯”班级足球联赛正如火如荼地举行,在高一年级某场比赛中,两个班级的比赛场地为矩形(如图),现已知矩形中米,米,宽为5米的足球门在边的中间放置.
(1)比赛中,同学甲在距离为18米,离为12米的地点处获得直接任意球机会,准备直接射门,求其有效射门角度;(求出的某个三角函数值即可)
(2)同学乙在边线上带球突破(视作点在边上移动),准备起脚向球门射门,求该同学应在何处(长为多少米时)射门角度最佳.(即使最大)
(以上问题不考虑场上其他因素)
18.自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
19.景区客栈的工作人员为了控制经营成本,减少浪费,合理安排入住游客的用餐,他们通过统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约600人;
③2月份入住客栈的游客约为200人,随后逐月递增直到8月份达到最多.
(1)若入住客栈的游客人数y与月份之间的关系可用函数(,,)近似描述,求该函数解析式;
(2)请问哪几个月份要准备多于650人的用餐?
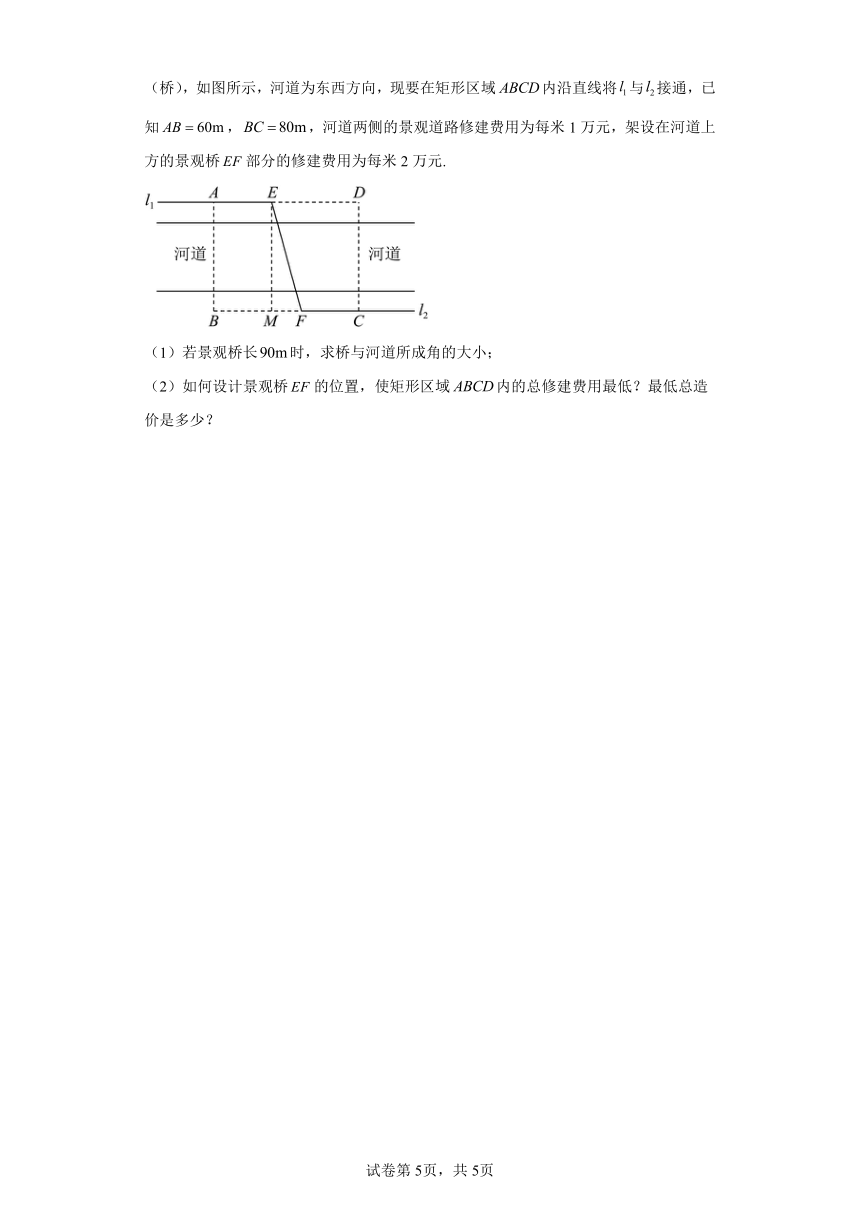
20.某城市为发展城市旅游经济,拟在景观河道的两侧,沿河岸直线与修建景观路(桥),如图所示,河道为东西方向,现要在矩形区域内沿直线将与接通,已知,,河道两侧的景观道路修建费用为每米1万元,架设在河道上方的景观桥部分的修建费用为每米2万元.
(1)若景观桥长时,求桥与河道所成角的大小;
(2)如何设计景观桥的位置,使矩形区域内的总修建费用最低?最低总造价是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】利用正弦函数性质及的面积,可得周期,然后求得.
【详解】由题意,所以,即周期为,
所以.
故选:D.
2.A
【分析】根据弧度制和终边相同角的定义判断即可.
【详解】如果我们把相等的角视为同一个角,则弧度制建立了一个从任意角的集合到实数集的一一对应的关系,故A正确,B错误,
终边相同的角的弧度制表示相差的整数倍,故C错误,D错误;
故选:A
3.B
【分析】分别求出两个扇形的面积,相减即可得解.
【详解】解:扇形的圆心角为
大扇形的面积为,
小扇形的面积为,
所以制作这样一面扇面需要的布料为.
故选:B.
4.A
【分析】由诱导公式结合三角函数的定义判断象限.
【详解】,即.
,只有第一象限满足,.
故选:A
5.B
【分析】首先根据平面向量平行的坐标表示可知,再根据余弦二倍角公式化简、解方程可得,进而可得,再根据两角差的正切公式即可求出结果.
【详解】因为,
所以,
所以,
所以,
所以或,
又,所以,
所以,所以.
故选:B.
【点睛】本题主要考查了平面向量共线的坐标运算,三角函数的同角关系,以及三角恒等变换求值,属于基础题.
6.B
【分析】先将两个函数变为同名的函数,然后利用三角函数图象变换的知识得出正确选项.
【详解】由于,
故需将的图象上所有的点,
向右平行移动个单位长度得到.
故选:B
7.C
【详解】由积化和差公式可得,则,由偶函数的图像的对称性可知,即或,也即 或.所以当时,不是偶函数,与已知题设不合;当时,则是偶函数,故,所以,又,故的图象可由函数的图象向左平方移个单位得到,应选答案C .
点睛:解答本题的难点在于如何取舍 或.解答时通过分类验证,从而求出函数的解析式和,使得问题获解.但在变形的过程中能变成的模样是较为困难的.
8.C
【分析】利用二倍角公式及两角差的正弦公式得到,再将两边平方及二倍角的正弦公式计算可得;
【详解】解:因为,即,所以,所以,所以,即,即,所以;
故选:C
9.ABD
【分析】根据函数的部分图象求出,,,再逐一判断各个选项即可.
【详解】解:由已知图象可得:,,解得,
,
,
图象过点,,可得,
可得:,,解得,,
当时,可得,可得,故正确;
由于,故正确;
由于,故错误;
由于,故正确.
故选:.
10.BC
【分析】根据两角和的余弦公式、二倍角公式和辅助角公式求出,利用正弦函数的性质依次求出最小正周期、最大值、对称轴和单调减区间即可.
【详解】
,
所以函数的最小正周期为,最大值为,故AD错误;
令,即对称轴为,故B正确;
令,解得,,
当时,函数的单调减区间为,
又,所以在上单调递减,故C正确.
故选:BC.
11.AC
【分析】将已知等式两边平方得,将配方,利用二倍角正弦公式可求出,可知A正确;利用二倍角的余弦公式求出,可知B不正确;由弦化切可得C正确;联立求出,可知D不正确.
【详解】因为,所以,所以,
所以,所以,
,故A正确;
由得,故B不正确;
由得,得,
得,得,故C正确;
联立,解得或,故D不正确.
故选:AC
12.AD
【分析】根据奇偶性定义判断A,周期性定义判断B,结合正弦函数、余弦函数性质判断CD.
【详解】,,显然且,因此是非奇非偶函数,A正确;
,因此不是函数的周期,B错;
由定义知,,时,,,时,,所以值域是,C错;
由上讨论知时,,时,,因此D正确.
故选:AD.
13.
【分析】根据二倍角的正弦公式及平方关系运算求解即可.
【详解】∵,
∴,
∴,
故答案为:.
14.
【分析】根据的图象可得到,及时的取值范围,结合余弦函数在上函数值符号的变化情况可得到不等式的解集.
【详解】由图象可知:时,;
当时,.
又余弦函数在时,时,
当时,,
故答案为:.
15.
【分析】根据三角函数的基本关系式,求得,结合,即可求解.
【详解】因为,
又因为,所以,
又由,所以,所以,
所以
,
所以
.
故答案为:.
16.
【分析】根据函数的奇偶性和单调性,列出不等式,解之即可.
【详解】因为的定义域为,定义域关于原点对称,
又,所以函数为偶函数,
当时,函数在上单调递增,且,
所以函数在上单调递减,在上单调递增,
又因为不等式,也即,
所以,则,因为,
所以,
故答案为:.
17.(1);(2).
【分析】(1)分别作,,,,由两角和的正切公式求得即得;
(2)设,,,,由两角差的正切公式求得,再结合基本不等式求得最大值可得.
【详解】(1)分别作,,垂足分别为,,
由题意可知米,米,米,米,所以米,米,在中,,在中,,
∴
(2)设,,,,
当且仅当时等号成立,此时最大,
所以该同学应在距离点为时射门角度最佳
18.(1)体力节律函数为:;情绪节律函数为:;节律函数为:;(2)处于体力节律高潮期,情绪节律低潮期,和智力节律临界日,适合参加体育竞技比赛
【分析】(1)根据三角函数周期直接得到答案.
(2)求得,代入函数分别计算得到答案.
【详解】(1)小英的体力节律周期为,故,故,故函数为:;同理可得情绪节律函数为:;智力节律函数为:.
(2)时间共有:.
当时,;;
.
故处于体力节律高潮期,情绪节律低潮期,和智力节律临界日,适合参加体育竞技比赛.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.
19.(1);(2)7,8,9三个月.
【分析】(1)由①确定周期求出,由②可求出A,由③知最小值,最大值,即可求出b,再代入特殊值求出,即可求得函数解析式;(2)根据题意列出不等式,利用正弦函数的图象与性质求解x的范围,再由可确定x可取的值,得解.
【详解】(1)因为函数为,
由①,周期,所以;
由②,最小,最大,且,故;
由③,在上递增,且,所以,
所以,解得,
又最小,最大,所以,则,
解得,由于,所以,
所以入住客栈的游客人数与月份之间的关系式为
.
(2)由条件可知,,化简得,
所以,
解得.因为,故.
即只有7,8,9三个月份要准备多于650人的用餐.
【点睛】本题考查函数的实际应用、正弦函数的图象与性质,属于中档题.
20.(1);(2)景观桥与和河道沿线所成的角为时,最低总造价是万元.
【分析】设与所成的角为(1)在△中有且,求角,进而求桥与河道所成角;(2)由题意可知总修建费用得到关于的函数,利用辅助角公式及正弦函数的性质即可求最低修建费用及景观桥的位置;
【详解】如题设中的图示,垂足为,设与所成的角为,即,故有,.
(1)当景观桥的长为时,得,即景观桥与和河道沿线所成的角为.
(2)由,可得总修建费用,
令,又,故,则且,又有,
所以最大值为,有最小值为,此时,景观桥与河道沿线所成的角为.
【点睛】本题考查了利用三角函数解决实际问题,结合辅助角公式及正弦函数的值域范围求最值问题,注意实际问题中的约束条件;
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选择:共40分.只有一项是符合题目要求的.
1.已知函数,点是曲线相邻的两个对称中心,点是的一个最值点,若的面积为1,则( )
A.1 B. C.2 D.
2.下列命题中正确的是( )
A.如果我们把相等的角视为同一个角,则弧度制建立了一个从任意角的集合到实数集的一一对应的关系
B.弧度制表示角时,不同大小的弧度可以表示同一个角
C.终边相同的角的弧度制表示相差
D.终边相同的角的弧度都相同
3.工艺扇面是中国书面一种常见的表现形式.某同学想用布料制作一面如图所示的扇面.已知扇面展开的中心角为,外圆半径为20cm,内圆半径为10cm.则制作这样一面扇面需要的布料为( )cm
A. B. C. D.
4.若,,则角的终边在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.已知,,,若,则( )
A. B. C. D.
6.要得到函数的图象,只需将函数的图象上所有的点( )
A.再向左平行移动个单位长度 B.再向右平行移动个单位长度
C.再向右平行移动个单位长度 D.再向左平行移动个单位长度
7.已知函数是偶函数,其中,则下列关于函数描述正确的是
A.在区间上的最小值为-1
B.的图象可由函数的图象先向上平移2个单位,再向右平移个单位得到
C.的图象可由函数的图象向左平方移个单位得到
D.的图象可由函数的图象向右平方移个单位得到
8.已知,则( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.如图是函数的部分图象,则下列选项正确的是( )
A. B.
C. D.
10.已知函数,则( )
A.最小正周期为 B.关于直线对称
C.在上单调递减 D.最大值为
11.已知,则( )
A. B.
C. D.
12.定义为a,b中较大的数,已知函数,给出下列命题:其中正确的为( )
A.为非奇非偶函数;
B.是以为最小正周期的周期函数;
C.的值域为;
D.当时,.
三、填空题(20分)
13.若,则 .
14.已知是定义在(0,3)上的函数,的图象如图所示,则不等式的解集是 .
15.已知,,则 .
16.已知函数,则不等式在上的解集为 .
四、解答题(70分)
17.在这春光明媚的季节里,2021江苏省梁丰高级中学“校长杯”班级足球联赛正如火如荼地举行,在高一年级某场比赛中,两个班级的比赛场地为矩形(如图),现已知矩形中米,米,宽为5米的足球门在边的中间放置.
(1)比赛中,同学甲在距离为18米,离为12米的地点处获得直接任意球机会,准备直接射门,求其有效射门角度;(求出的某个三角函数值即可)
(2)同学乙在边线上带球突破(视作点在边上移动),准备起脚向球门射门,求该同学应在何处(长为多少米时)射门角度最佳.(即使最大)
(以上问题不考虑场上其他因素)
18.自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
19.景区客栈的工作人员为了控制经营成本,减少浪费,合理安排入住游客的用餐,他们通过统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约600人;
③2月份入住客栈的游客约为200人,随后逐月递增直到8月份达到最多.
(1)若入住客栈的游客人数y与月份之间的关系可用函数(,,)近似描述,求该函数解析式;
(2)请问哪几个月份要准备多于650人的用餐?
20.某城市为发展城市旅游经济,拟在景观河道的两侧,沿河岸直线与修建景观路(桥),如图所示,河道为东西方向,现要在矩形区域内沿直线将与接通,已知,,河道两侧的景观道路修建费用为每米1万元,架设在河道上方的景观桥部分的修建费用为每米2万元.
(1)若景观桥长时,求桥与河道所成角的大小;
(2)如何设计景观桥的位置,使矩形区域内的总修建费用最低?最低总造价是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】利用正弦函数性质及的面积,可得周期,然后求得.
【详解】由题意,所以,即周期为,
所以.
故选:D.
2.A
【分析】根据弧度制和终边相同角的定义判断即可.
【详解】如果我们把相等的角视为同一个角,则弧度制建立了一个从任意角的集合到实数集的一一对应的关系,故A正确,B错误,
终边相同的角的弧度制表示相差的整数倍,故C错误,D错误;
故选:A
3.B
【分析】分别求出两个扇形的面积,相减即可得解.
【详解】解:扇形的圆心角为
大扇形的面积为,
小扇形的面积为,
所以制作这样一面扇面需要的布料为.
故选:B.
4.A
【分析】由诱导公式结合三角函数的定义判断象限.
【详解】,即.
,只有第一象限满足,.
故选:A
5.B
【分析】首先根据平面向量平行的坐标表示可知,再根据余弦二倍角公式化简、解方程可得,进而可得,再根据两角差的正切公式即可求出结果.
【详解】因为,
所以,
所以,
所以,
所以或,
又,所以,
所以,所以.
故选:B.
【点睛】本题主要考查了平面向量共线的坐标运算,三角函数的同角关系,以及三角恒等变换求值,属于基础题.
6.B
【分析】先将两个函数变为同名的函数,然后利用三角函数图象变换的知识得出正确选项.
【详解】由于,
故需将的图象上所有的点,
向右平行移动个单位长度得到.
故选:B
7.C
【详解】由积化和差公式可得,则,由偶函数的图像的对称性可知,即或,也即 或.所以当时,不是偶函数,与已知题设不合;当时,则是偶函数,故,所以,又,故的图象可由函数的图象向左平方移个单位得到,应选答案C .
点睛:解答本题的难点在于如何取舍 或.解答时通过分类验证,从而求出函数的解析式和,使得问题获解.但在变形的过程中能变成的模样是较为困难的.
8.C
【分析】利用二倍角公式及两角差的正弦公式得到,再将两边平方及二倍角的正弦公式计算可得;
【详解】解:因为,即,所以,所以,所以,即,即,所以;
故选:C
9.ABD
【分析】根据函数的部分图象求出,,,再逐一判断各个选项即可.
【详解】解:由已知图象可得:,,解得,
,
,
图象过点,,可得,
可得:,,解得,,
当时,可得,可得,故正确;
由于,故正确;
由于,故错误;
由于,故正确.
故选:.
10.BC
【分析】根据两角和的余弦公式、二倍角公式和辅助角公式求出,利用正弦函数的性质依次求出最小正周期、最大值、对称轴和单调减区间即可.
【详解】
,
所以函数的最小正周期为,最大值为,故AD错误;
令,即对称轴为,故B正确;
令,解得,,
当时,函数的单调减区间为,
又,所以在上单调递减,故C正确.
故选:BC.
11.AC
【分析】将已知等式两边平方得,将配方,利用二倍角正弦公式可求出,可知A正确;利用二倍角的余弦公式求出,可知B不正确;由弦化切可得C正确;联立求出,可知D不正确.
【详解】因为,所以,所以,
所以,所以,
,故A正确;
由得,故B不正确;
由得,得,
得,得,故C正确;
联立,解得或,故D不正确.
故选:AC
12.AD
【分析】根据奇偶性定义判断A,周期性定义判断B,结合正弦函数、余弦函数性质判断CD.
【详解】,,显然且,因此是非奇非偶函数,A正确;
,因此不是函数的周期,B错;
由定义知,,时,,,时,,所以值域是,C错;
由上讨论知时,,时,,因此D正确.
故选:AD.
13.
【分析】根据二倍角的正弦公式及平方关系运算求解即可.
【详解】∵,
∴,
∴,
故答案为:.
14.
【分析】根据的图象可得到,及时的取值范围,结合余弦函数在上函数值符号的变化情况可得到不等式的解集.
【详解】由图象可知:时,;
当时,.
又余弦函数在时,时,
当时,,
故答案为:.
15.
【分析】根据三角函数的基本关系式,求得,结合,即可求解.
【详解】因为,
又因为,所以,
又由,所以,所以,
所以
,
所以
.
故答案为:.
16.
【分析】根据函数的奇偶性和单调性,列出不等式,解之即可.
【详解】因为的定义域为,定义域关于原点对称,
又,所以函数为偶函数,
当时,函数在上单调递增,且,
所以函数在上单调递减,在上单调递增,
又因为不等式,也即,
所以,则,因为,
所以,
故答案为:.
17.(1);(2).
【分析】(1)分别作,,,,由两角和的正切公式求得即得;
(2)设,,,,由两角差的正切公式求得,再结合基本不等式求得最大值可得.
【详解】(1)分别作,,垂足分别为,,
由题意可知米,米,米,米,所以米,米,在中,,在中,,
∴
(2)设,,,,
当且仅当时等号成立,此时最大,
所以该同学应在距离点为时射门角度最佳
18.(1)体力节律函数为:;情绪节律函数为:;节律函数为:;(2)处于体力节律高潮期,情绪节律低潮期,和智力节律临界日,适合参加体育竞技比赛
【分析】(1)根据三角函数周期直接得到答案.
(2)求得,代入函数分别计算得到答案.
【详解】(1)小英的体力节律周期为,故,故,故函数为:;同理可得情绪节律函数为:;智力节律函数为:.
(2)时间共有:.
当时,;;
.
故处于体力节律高潮期,情绪节律低潮期,和智力节律临界日,适合参加体育竞技比赛.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.
19.(1);(2)7,8,9三个月.
【分析】(1)由①确定周期求出,由②可求出A,由③知最小值,最大值,即可求出b,再代入特殊值求出,即可求得函数解析式;(2)根据题意列出不等式,利用正弦函数的图象与性质求解x的范围,再由可确定x可取的值,得解.
【详解】(1)因为函数为,
由①,周期,所以;
由②,最小,最大,且,故;
由③,在上递增,且,所以,
所以,解得,
又最小,最大,所以,则,
解得,由于,所以,
所以入住客栈的游客人数与月份之间的关系式为
.
(2)由条件可知,,化简得,
所以,
解得.因为,故.
即只有7,8,9三个月份要准备多于650人的用餐.
【点睛】本题考查函数的实际应用、正弦函数的图象与性质,属于中档题.
20.(1);(2)景观桥与和河道沿线所成的角为时,最低总造价是万元.
【分析】设与所成的角为(1)在△中有且,求角,进而求桥与河道所成角;(2)由题意可知总修建费用得到关于的函数,利用辅助角公式及正弦函数的性质即可求最低修建费用及景观桥的位置;
【详解】如题设中的图示,垂足为,设与所成的角为,即,故有,.
(1)当景观桥的长为时,得,即景观桥与和河道沿线所成的角为.
(2)由,可得总修建费用,
令,又,故,则且,又有,
所以最大值为,有最小值为,此时,景观桥与河道沿线所成的角为.
【点睛】本题考查了利用三角函数解决实际问题,结合辅助角公式及正弦函数的值域范围求最值问题,注意实际问题中的约束条件;
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
