高中数学新人教A版选择性必修第一册 期末测试(含解析)
文档属性
| 名称 | 高中数学新人教A版选择性必修第一册 期末测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览




文档简介
高中数学新人教A版选择性必修第一册 期末测试
学校:___________姓名:___________班级:___________考号:___________
一、单选择:共40分.只有一项是符合题目要求的.
1.直线的斜率为( )
A. B. C. D.
2.已知椭圆的两个焦点分别为,,P为椭圆上一点,的平分线与x轴交于点,作交于点H,则等于( )
A.3 B.4 C.5 D.6
3.已知定圆,定圆,动圆圆与定圆都内切,则动圆的圆心的轨迹方程为( )
A. B. C. D.
4.已知椭圆:,左、右焦点分别为,过的直线交椭圆于两点,若的最大值为5,则的值是
A.1 B. C. D.
5.直线的倾斜角为( )
A. B. C. D.
6.已知过抛物线的焦点的直线交抛物线于两点,线段的延长线交抛物线的准线于点,若,则( )
A.3 B.4 C.6 D.8
7.抛物线的焦点坐标为( )
A. B. C. D.
8.直线与圆交于A,B两点,则( )
A.2 B. C.4 D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知直线,其中,下列说法正确的是( ).
A.若直线与直线平行,则
B.当时,直线与直线垂直
C.当时,直线在两坐标轴上的截距相等
D.直线过定点
10.对于抛物线,下列描述不正确的是( )
A.开口向上,焦点为 B.开口向上,焦点为
C.准线方程为 D.准线方程为
11.已知抛物线与圆交于两点,且,直线过的焦点,且与交于两点,则下列说法中正确的是( )
A.若直线的斜率为,则
B.的最小值为
C.若以为直径的圆与轴的公共点为,则的横坐标为
D.若点,则周长的最小值为
12.如图,在三棱柱中,底面是等边三角形,侧棱底面,为的中点,若,,则( )
A.
B.异面直线与所成角的余弦值为
C.异面直线与所成角的余弦值为
D.平面
三、填空题(20分)
13.已知,,若,,且平面,则 .
14.已知椭圆的左焦点为,右焦点为.若椭圆上存在一点,满足线段相切于以椭圆的短轴为直径的圆,切点为线段的中点,则该椭圆的离心率为 .
15.已知抛物线过点,则抛物线的准线方程为 .
16.在直角三角形中,,椭圆的一个焦点为C,另一个焦点在边上,并且椭圆经过点,则椭圆的长轴长等于 .
四、解答题(70分)
17.外形是双曲面的冷却塔具有众多优点,如自然通风和散热效果好,结构强度和抗变形能力强等,其设计原理涉及到物理学、建筑学等学科知识.如图1是中国华电集团的某个火力发电厂的一座冷却塔,它的外形可以看成是由一条双曲线的一部分绕着它的虚轴所在直线旋转而成,其轴截面如图2所示.已知下口圆面的直径为80米,上口圆面的直径为40米,高为90米,下口到最小直径圆面的距离为80米.
(1)求最小直径圆面的面积;
(2)双曲面也是直纹曲面,即可以看成是由一条直线绕另一条直线旋转而成,该直线叫做双曲面的直母线.过双曲面上的任意一点有且只有两条相交的直母线(如图3),对于任意一条直母线,均存在一个轴截面和它平行,此轴截面截双曲面所得的双曲线有两条渐近线,且直母线与其中一条平行.广州电视塔(昵称“小蛮腰”,如图4)就是根据这一理论设计的,极大地方便了建造、节约了成本(主钢梁在直母线上,钢筋不需要弯曲).若图1中的冷却塔也采用直母线主钢梁,求主钢梁的长度(精确到0.01米,参考数据:).
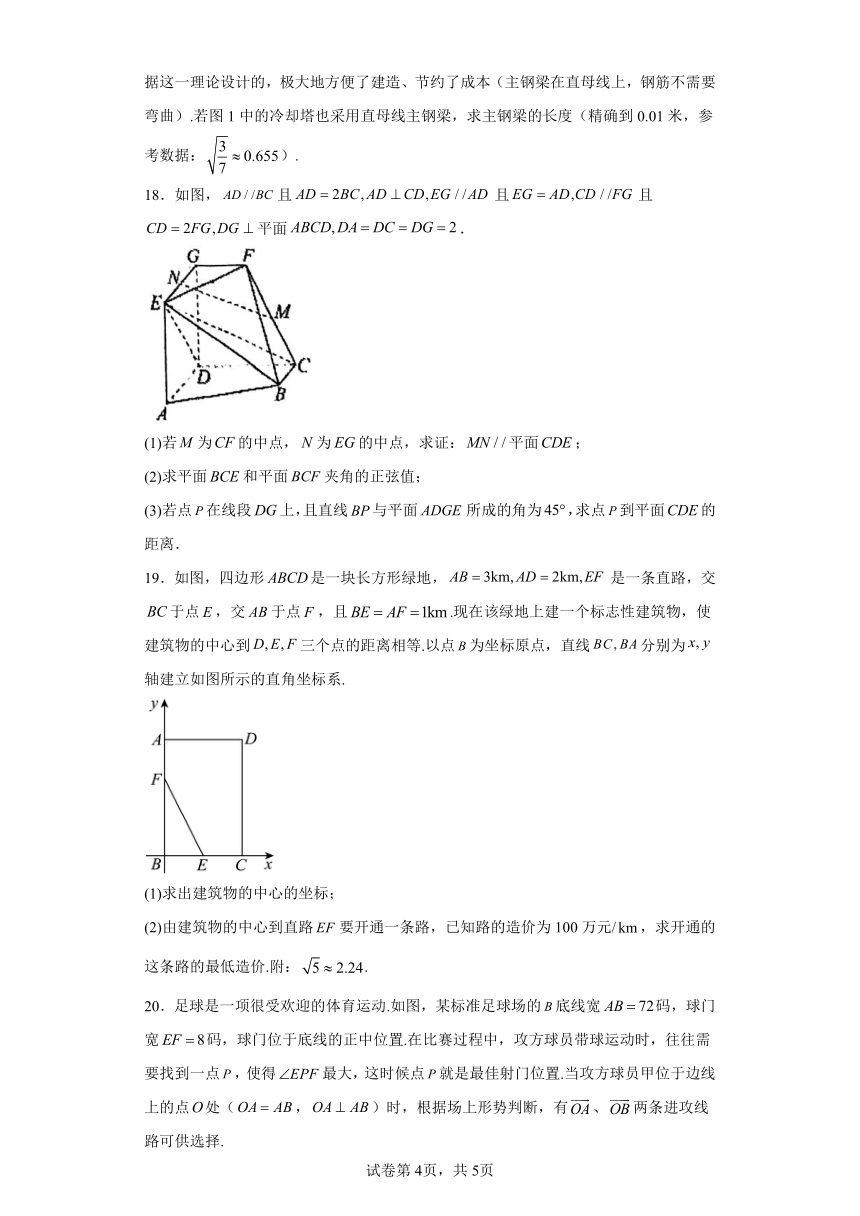
18.如图,且且且平面.
(1)若为的中点,为的中点,求证:平面;
(2)求平面和平面夹角的正弦值;
(3)若点在线段上,且直线与平面所成的角为,求点到平面的距离.
19.如图,四边形是一块长方形绿地,是一条直路,交于点,交于点,且.现在该绿地上建一个标志性建筑物,使建筑物的中心到三个点的距离相等.以点为坐标原点,直线分别为轴建立如图所示的直角坐标系.
(1)求出建筑物的中心的坐标;
(2)由建筑物的中心到直路要开通一条路,已知路的造价为100万元/,求开通的这条路的最低造价.附:.
20.足球是一项很受欢迎的体育运动.如图,某标准足球场的底线宽码,球门宽码,球门位于底线的正中位置.在比赛过程中,攻方球员带球运动时,往往需要找到一点,使得最大,这时候点就是最佳射门位置.当攻方球员甲位于边线上的点处(,)时,根据场上形势判断,有、两条进攻线路可供选择.
(1)若选择线路,则甲带球多少码时,到达最佳射门位置;
(2)若选择线路,则甲带球多少码时,到达最佳射门位置.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】把直线方程化为斜截式后可得斜率.
【详解】直线方程的斜截式为:,斜率为.
故选:D.
2.A
【分析】根据角平分线的性质和椭圆的定义可求.
【详解】如图,根据题意,有,且.
由角平分线定理和椭圆的定义,有
因此是以为斜边的直角三角形,
进而可得,因此.
3.A
【分析】根据圆与圆的位置关系的判定方法,结合双曲线的定义即可判断答案.
【详解】由题意,设动圆的圆心为,半径为r,圆的圆心为,半径为1,圆的圆心为,半径为5.
而圆与定圆都内切,所以,,则.于是,动圆的圆心的轨迹为以,为焦点的双曲线的右支,则,故动圆的圆心的轨迹方程为.
故选:A.
4.D
【分析】由题意可知椭圆是焦点在x轴上的椭圆,利用椭圆定义得到|BF2|+|AF2|=8﹣|AB|,再由过椭圆焦点的弦中通径的长最短,可知当AB垂直于x轴时|AB|最小,把|AB|的最小值b2代入|BF2|+|AF2|=8﹣|AB|,由|BF2|+|AF2|的最大值等于5列式求b的值即可.
【详解】由0<b<2可知,焦点在x轴上,
∵过F1的直线l交椭圆于A,B两点,
则|BF2|+|AF2|+|BF1|+|AF1|=2a+2a=4a=8
∴|BF2|+|AF2|=8﹣|AB|.
当AB垂直x轴时|AB|最小,|BF2|+|AF2|值最大,
此时|AB|=b2,则5=8﹣b2,
解得b,
故选D.
【点睛】本题考查直线与圆锥曲线的关系,考查了椭圆的定义,考查椭圆的通径公式,考查计算能力,属于中档题.
5.B
【分析】设直线的倾斜角为,由直线的方程可得其斜率,则有,结合θ的范围即可得答案.
【详解】解:根据题意,设直线的倾斜角为θ,
因直线的方程为,故其斜率,则有,
又由,则,
故选:B.
6.B
【分析】过作准线的垂线,垂足分别为,利用抛物线的定义得线段长关系,利用平行线性质得比例式,求得后可得弦长.
【详解】过作准线的垂线,垂足分别为,则,
,,记,
由得即,解得,所以.
故选:B.
【点睛】关键点点睛:本题考查抛物线的焦点弦长,解题关键是利用抛物线的定义把点到焦点的距离转化为到准线的距离,然后由平面几何知识求解.
7.C
【分析】化抛物线方程为标准方程后可得焦点坐标.
【详解】可化为,故,
焦点为,即为,
故选:C.
8.C
【分析】求出圆心、半径,再求出圆心到直线的距离,利用可得答案..
【详解】由配方得,
所以圆心为,半径为3,圆心到直线的距离,
所以,.
故选:C.
9.BD
【分析】根据直线的平行关系可求得a,判断A;利用直线斜率与垂直的关系判断B;求出直线在坐标轴上的截距判断C;求出直线l所过定点判断D.
【详解】对于A,直线与直线平行,则,即,
解得或,A错误;
对于B,当时,直线为,
直线与斜率之积为,此时直线与直线垂直,B正确;
对于C,当时,为,
直线在x轴上截距为,在y轴上截距为1,二者不相等,C错误;
对于D,即,
由于,令,则,即直线过定点,D正确,
故选:BD
10.BC
【分析】把抛物线的方程化为标准方程,结合性质可得答案.
【详解】因为,所以,所以抛物线开口向上,焦点为,其准线方程为,结合选项可得A,D正确.
故选:BC.
11.ABC
【分析】首先求出抛物线的解析式,设出MN方程联立进行求解当时,,进而判断选项A;再根据韦达定理和不等式求最小值后判断选项B;画出大致图像过点M作准线的垂线,垂足为,交y轴于,结合抛物线定义判断选项C;过G作GH垂直于准线,垂足为H,结合的周长为进而判断选项D即可.
【详解】解:由题意得点在抛物线上,
所以,解得,所以C:,则,
对于A选项,设直线:,与联立得,
设,,所以,,
所以,
当直线的斜率为时,,,故A项正确;
对于B选项,由抛物线的定义, ,
所以,
当且仅当,时等号成立,故B项正确;
对于C选项,如图,过点作准线的垂线,垂足为,交轴于,
取的中点为,过点作轴的垂线,垂足为,
则,是梯形的中位线,
由抛物线的定义可得,
所以,
所以以为直径的圆与轴相切,
所以为圆与轴的切点,所以点的纵坐标为,
又因为为的中点,所以点的纵坐标为,
又点在抛物线上,所以点的横坐标为,故C项正确;
对于D选项,过作垂直于准线,垂足为,
所以的周长为,
当且仅当点的坐标为时取等号,故D项错误.
故选:ABC.
12.AC
【分析】由线面垂直的判定法则可得平面,从而可证明A;建立空间直角坐标系,求出与的方向向量,即可求出两直线所成角的余弦值,求出平面的法向量与的方向向量,从而可判断直线和平面是否平行.
【详解】A:因为侧棱底面,所以,因为是等边三角形,,
所以,因为,所以平面,则, A正确;
以为原点,如图建立空间直角坐标系,则,,,
,所以,,
所以,
所以异面直线与所成角的余弦值为,B不正确,C正确;
又因为,,设平面法向量为,
则,即 ,取,则,
因为,且,所以若平面不成立,D不正确;
故选:AC.
【点睛】本题考查了线面垂直的判定,考查了线面平行的判定,考查了异面直线所成角的求解,属于中档题.本题的关键是建立空间坐标系,结合向量进行求解.
13.
【分析】依题意可得,即可求出,再根据线面垂直得到,,由数量积的坐标表示得到方程组,解得即可.
【详解】因为,所以,所以,所以,
又因为平面,平面,所以,,
所以,解得,因此.
故答案为:
14.
【分析】由几何关系得,结合椭圆定义与勾股定理列方程求解
【详解】因为线段相切于以椭圆的短轴为直径的圆,切点为线段的中点,
则,,
设,由椭圆的定义,得,
由勾股定理得,解得,所以椭圆的离心率.
故答案为:
15.
【解析】代入求解抛物线,再化简成标准形式求解准线方程即可.
【详解】由题, ,故.故抛物线的准线方程为.
故答案为:
【点睛】本题主要考查了根据抛物线上的点抛物线方程以及准线的问题.属于基础题.
16.
【解析】利用勾股定理求出,然后在焦点三角形中,利用椭圆的定义表示出和,根据列式计算长轴长.
【详解】解:如图,设椭圆的长轴长为,因为,则,
,,则,所以.
故答案为:
17.(1);(2)
【分析】由题设,则有在双曲线上,代入得解双曲线方程,得到最小直径圆面是以双曲线的实轴为直径的圆面得解
(2)求得一条渐近线方程为 ,由题意知上下轴截面平行且直母线与渐近线其中一条平行,所以四边形是平行四边形,求得得解
【详解】
由题设,则有在双曲线上,所以
解得
因为最小直径圆面是以双曲线的实轴为直径的圆面
此时圆面的面积为
(2)由(1)问得:的一条渐近线方程为
如图由题意知上下轴截面平行且直母线与渐近线其中一条平行,所以四边形是平行四边形,所以所求主钢梁的长度即为
【点睛】建立适当坐标系得到双曲线方程,利用直母线与渐近线其中一条平行,得到四边形是平行四边形是解题关键.
18.(1)证明见解析;
(2);
(3).
【分析】(1)取GD中点为Q,连接NQ,MQ,通过证明平面平面,可得平面;(2)如图,建立以D为原点的空间直角坐标系,分别求出平面和平面夹角的法向量,即可得答案;(3)由(2),设,直线与平面所成的角为可得点P坐标,可得点到平面的距离.
【详解】(1)取GD中点为Q,连接NQ,MQ.
因为的中点,为的中点,Q为GD中点,
由三角形及梯形中位线定理,可得.
又注意到,平面EDC,平面EDC,
平面MNQ,,则平面平面.
又平面MQN,则平面.
(2)因平面ABCD,平面ABCD,
则,又,则如图建立以D为原点的空间坐标系.
则.
.
设平面和平面的法向量分别为.
则,取;
,取.
设平面和平面夹角为,则.
则平面和平面夹角的正弦值为.
(3)由(2),设,其中,则
又由题可得,平面的一个法向量可取.
结合直线与平面所成的角为,
则.
则,.
设平面法向量为,则.
取,则点到平面的距离.
19.(1)
(2)112万元
【分析】(1)设出过点的圆的一般方程,代入三个点的坐标,待定系数法求出圆的一般方程,化为标准方程,得到圆心,即建筑物的中心的坐标;
(2)求出,由垂径定理得到点到的距离,从而求出开通的这条路的最低造价.
【详解】(1)由题可知,
由题可知经过点的圆的圆心即为所建建筑物的中心,
设圆的方程为,
则,解得,
圆的方程为,即,
建筑物的中心的坐标为.
(2)因为为建筑物的中心坐标,
设线段EF的中点为Q,由垂径定理得HQ的长度为点H到EF的最小距离,
,圆的半径为,
点到的距离为,
开通的这条路的最低造价为(万元).
20.(1)
(2)
【分析】(1)先由题意表示出,,然后表示出,从而利用基本不等式求出的最大值,进而得到取得最大值时点的位置;
(2)建立平面直角坐标系,从而利用斜率公式表示出,,然后表示出,从而利用基本不等式求出的最大值,进而得到取得最大值时点的位置.
【详解】(1)若选择线路,设,其中,,,
则,,
所以
,
当且仅当时,即当时,等号成立,此时,
由题意知,因为函数在上单调递增,
所以最大时,最大,
所以,若选择线路,则甲带球码时,到达最佳射门位置.
(2)若选择线路,以线段的中点为坐标原点,、的方向分别为、轴的正方向建立如图所示的平面直角坐标系,
则,,,,
则,直线的方程为,
设点,其中,
,,
所以
,
令,则,
所以,
当且仅当,即,即时,等号成立,
所以,
当且仅当时,等号成立,此时,,
由题意知,因为函数在上单调递增,
所以最大时,最大,
所以,若选择线路,则甲带球码时,到达最佳射门位置.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选择:共40分.只有一项是符合题目要求的.
1.直线的斜率为( )
A. B. C. D.
2.已知椭圆的两个焦点分别为,,P为椭圆上一点,的平分线与x轴交于点,作交于点H,则等于( )
A.3 B.4 C.5 D.6
3.已知定圆,定圆,动圆圆与定圆都内切,则动圆的圆心的轨迹方程为( )
A. B. C. D.
4.已知椭圆:,左、右焦点分别为,过的直线交椭圆于两点,若的最大值为5,则的值是
A.1 B. C. D.
5.直线的倾斜角为( )
A. B. C. D.
6.已知过抛物线的焦点的直线交抛物线于两点,线段的延长线交抛物线的准线于点,若,则( )
A.3 B.4 C.6 D.8
7.抛物线的焦点坐标为( )
A. B. C. D.
8.直线与圆交于A,B两点,则( )
A.2 B. C.4 D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知直线,其中,下列说法正确的是( ).
A.若直线与直线平行,则
B.当时,直线与直线垂直
C.当时,直线在两坐标轴上的截距相等
D.直线过定点
10.对于抛物线,下列描述不正确的是( )
A.开口向上,焦点为 B.开口向上,焦点为
C.准线方程为 D.准线方程为
11.已知抛物线与圆交于两点,且,直线过的焦点,且与交于两点,则下列说法中正确的是( )
A.若直线的斜率为,则
B.的最小值为
C.若以为直径的圆与轴的公共点为,则的横坐标为
D.若点,则周长的最小值为
12.如图,在三棱柱中,底面是等边三角形,侧棱底面,为的中点,若,,则( )
A.
B.异面直线与所成角的余弦值为
C.异面直线与所成角的余弦值为
D.平面
三、填空题(20分)
13.已知,,若,,且平面,则 .
14.已知椭圆的左焦点为,右焦点为.若椭圆上存在一点,满足线段相切于以椭圆的短轴为直径的圆,切点为线段的中点,则该椭圆的离心率为 .
15.已知抛物线过点,则抛物线的准线方程为 .
16.在直角三角形中,,椭圆的一个焦点为C,另一个焦点在边上,并且椭圆经过点,则椭圆的长轴长等于 .
四、解答题(70分)
17.外形是双曲面的冷却塔具有众多优点,如自然通风和散热效果好,结构强度和抗变形能力强等,其设计原理涉及到物理学、建筑学等学科知识.如图1是中国华电集团的某个火力发电厂的一座冷却塔,它的外形可以看成是由一条双曲线的一部分绕着它的虚轴所在直线旋转而成,其轴截面如图2所示.已知下口圆面的直径为80米,上口圆面的直径为40米,高为90米,下口到最小直径圆面的距离为80米.
(1)求最小直径圆面的面积;
(2)双曲面也是直纹曲面,即可以看成是由一条直线绕另一条直线旋转而成,该直线叫做双曲面的直母线.过双曲面上的任意一点有且只有两条相交的直母线(如图3),对于任意一条直母线,均存在一个轴截面和它平行,此轴截面截双曲面所得的双曲线有两条渐近线,且直母线与其中一条平行.广州电视塔(昵称“小蛮腰”,如图4)就是根据这一理论设计的,极大地方便了建造、节约了成本(主钢梁在直母线上,钢筋不需要弯曲).若图1中的冷却塔也采用直母线主钢梁,求主钢梁的长度(精确到0.01米,参考数据:).
18.如图,且且且平面.
(1)若为的中点,为的中点,求证:平面;
(2)求平面和平面夹角的正弦值;
(3)若点在线段上,且直线与平面所成的角为,求点到平面的距离.
19.如图,四边形是一块长方形绿地,是一条直路,交于点,交于点,且.现在该绿地上建一个标志性建筑物,使建筑物的中心到三个点的距离相等.以点为坐标原点,直线分别为轴建立如图所示的直角坐标系.
(1)求出建筑物的中心的坐标;
(2)由建筑物的中心到直路要开通一条路,已知路的造价为100万元/,求开通的这条路的最低造价.附:.
20.足球是一项很受欢迎的体育运动.如图,某标准足球场的底线宽码,球门宽码,球门位于底线的正中位置.在比赛过程中,攻方球员带球运动时,往往需要找到一点,使得最大,这时候点就是最佳射门位置.当攻方球员甲位于边线上的点处(,)时,根据场上形势判断,有、两条进攻线路可供选择.
(1)若选择线路,则甲带球多少码时,到达最佳射门位置;
(2)若选择线路,则甲带球多少码时,到达最佳射门位置.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】把直线方程化为斜截式后可得斜率.
【详解】直线方程的斜截式为:,斜率为.
故选:D.
2.A
【分析】根据角平分线的性质和椭圆的定义可求.
【详解】如图,根据题意,有,且.
由角平分线定理和椭圆的定义,有
因此是以为斜边的直角三角形,
进而可得,因此.
3.A
【分析】根据圆与圆的位置关系的判定方法,结合双曲线的定义即可判断答案.
【详解】由题意,设动圆的圆心为,半径为r,圆的圆心为,半径为1,圆的圆心为,半径为5.
而圆与定圆都内切,所以,,则.于是,动圆的圆心的轨迹为以,为焦点的双曲线的右支,则,故动圆的圆心的轨迹方程为.
故选:A.
4.D
【分析】由题意可知椭圆是焦点在x轴上的椭圆,利用椭圆定义得到|BF2|+|AF2|=8﹣|AB|,再由过椭圆焦点的弦中通径的长最短,可知当AB垂直于x轴时|AB|最小,把|AB|的最小值b2代入|BF2|+|AF2|=8﹣|AB|,由|BF2|+|AF2|的最大值等于5列式求b的值即可.
【详解】由0<b<2可知,焦点在x轴上,
∵过F1的直线l交椭圆于A,B两点,
则|BF2|+|AF2|+|BF1|+|AF1|=2a+2a=4a=8
∴|BF2|+|AF2|=8﹣|AB|.
当AB垂直x轴时|AB|最小,|BF2|+|AF2|值最大,
此时|AB|=b2,则5=8﹣b2,
解得b,
故选D.
【点睛】本题考查直线与圆锥曲线的关系,考查了椭圆的定义,考查椭圆的通径公式,考查计算能力,属于中档题.
5.B
【分析】设直线的倾斜角为,由直线的方程可得其斜率,则有,结合θ的范围即可得答案.
【详解】解:根据题意,设直线的倾斜角为θ,
因直线的方程为,故其斜率,则有,
又由,则,
故选:B.
6.B
【分析】过作准线的垂线,垂足分别为,利用抛物线的定义得线段长关系,利用平行线性质得比例式,求得后可得弦长.
【详解】过作准线的垂线,垂足分别为,则,
,,记,
由得即,解得,所以.
故选:B.
【点睛】关键点点睛:本题考查抛物线的焦点弦长,解题关键是利用抛物线的定义把点到焦点的距离转化为到准线的距离,然后由平面几何知识求解.
7.C
【分析】化抛物线方程为标准方程后可得焦点坐标.
【详解】可化为,故,
焦点为,即为,
故选:C.
8.C
【分析】求出圆心、半径,再求出圆心到直线的距离,利用可得答案..
【详解】由配方得,
所以圆心为,半径为3,圆心到直线的距离,
所以,.
故选:C.
9.BD
【分析】根据直线的平行关系可求得a,判断A;利用直线斜率与垂直的关系判断B;求出直线在坐标轴上的截距判断C;求出直线l所过定点判断D.
【详解】对于A,直线与直线平行,则,即,
解得或,A错误;
对于B,当时,直线为,
直线与斜率之积为,此时直线与直线垂直,B正确;
对于C,当时,为,
直线在x轴上截距为,在y轴上截距为1,二者不相等,C错误;
对于D,即,
由于,令,则,即直线过定点,D正确,
故选:BD
10.BC
【分析】把抛物线的方程化为标准方程,结合性质可得答案.
【详解】因为,所以,所以抛物线开口向上,焦点为,其准线方程为,结合选项可得A,D正确.
故选:BC.
11.ABC
【分析】首先求出抛物线的解析式,设出MN方程联立进行求解当时,,进而判断选项A;再根据韦达定理和不等式求最小值后判断选项B;画出大致图像过点M作准线的垂线,垂足为,交y轴于,结合抛物线定义判断选项C;过G作GH垂直于准线,垂足为H,结合的周长为进而判断选项D即可.
【详解】解:由题意得点在抛物线上,
所以,解得,所以C:,则,
对于A选项,设直线:,与联立得,
设,,所以,,
所以,
当直线的斜率为时,,,故A项正确;
对于B选项,由抛物线的定义, ,
所以,
当且仅当,时等号成立,故B项正确;
对于C选项,如图,过点作准线的垂线,垂足为,交轴于,
取的中点为,过点作轴的垂线,垂足为,
则,是梯形的中位线,
由抛物线的定义可得,
所以,
所以以为直径的圆与轴相切,
所以为圆与轴的切点,所以点的纵坐标为,
又因为为的中点,所以点的纵坐标为,
又点在抛物线上,所以点的横坐标为,故C项正确;
对于D选项,过作垂直于准线,垂足为,
所以的周长为,
当且仅当点的坐标为时取等号,故D项错误.
故选:ABC.
12.AC
【分析】由线面垂直的判定法则可得平面,从而可证明A;建立空间直角坐标系,求出与的方向向量,即可求出两直线所成角的余弦值,求出平面的法向量与的方向向量,从而可判断直线和平面是否平行.
【详解】A:因为侧棱底面,所以,因为是等边三角形,,
所以,因为,所以平面,则, A正确;
以为原点,如图建立空间直角坐标系,则,,,
,所以,,
所以,
所以异面直线与所成角的余弦值为,B不正确,C正确;
又因为,,设平面法向量为,
则,即 ,取,则,
因为,且,所以若平面不成立,D不正确;
故选:AC.
【点睛】本题考查了线面垂直的判定,考查了线面平行的判定,考查了异面直线所成角的求解,属于中档题.本题的关键是建立空间坐标系,结合向量进行求解.
13.
【分析】依题意可得,即可求出,再根据线面垂直得到,,由数量积的坐标表示得到方程组,解得即可.
【详解】因为,所以,所以,所以,
又因为平面,平面,所以,,
所以,解得,因此.
故答案为:
14.
【分析】由几何关系得,结合椭圆定义与勾股定理列方程求解
【详解】因为线段相切于以椭圆的短轴为直径的圆,切点为线段的中点,
则,,
设,由椭圆的定义,得,
由勾股定理得,解得,所以椭圆的离心率.
故答案为:
15.
【解析】代入求解抛物线,再化简成标准形式求解准线方程即可.
【详解】由题, ,故.故抛物线的准线方程为.
故答案为:
【点睛】本题主要考查了根据抛物线上的点抛物线方程以及准线的问题.属于基础题.
16.
【解析】利用勾股定理求出,然后在焦点三角形中,利用椭圆的定义表示出和,根据列式计算长轴长.
【详解】解:如图,设椭圆的长轴长为,因为,则,
,,则,所以.
故答案为:
17.(1);(2)
【分析】由题设,则有在双曲线上,代入得解双曲线方程,得到最小直径圆面是以双曲线的实轴为直径的圆面得解
(2)求得一条渐近线方程为 ,由题意知上下轴截面平行且直母线与渐近线其中一条平行,所以四边形是平行四边形,求得得解
【详解】
由题设,则有在双曲线上,所以
解得
因为最小直径圆面是以双曲线的实轴为直径的圆面
此时圆面的面积为
(2)由(1)问得:的一条渐近线方程为
如图由题意知上下轴截面平行且直母线与渐近线其中一条平行,所以四边形是平行四边形,所以所求主钢梁的长度即为
【点睛】建立适当坐标系得到双曲线方程,利用直母线与渐近线其中一条平行,得到四边形是平行四边形是解题关键.
18.(1)证明见解析;
(2);
(3).
【分析】(1)取GD中点为Q,连接NQ,MQ,通过证明平面平面,可得平面;(2)如图,建立以D为原点的空间直角坐标系,分别求出平面和平面夹角的法向量,即可得答案;(3)由(2),设,直线与平面所成的角为可得点P坐标,可得点到平面的距离.
【详解】(1)取GD中点为Q,连接NQ,MQ.
因为的中点,为的中点,Q为GD中点,
由三角形及梯形中位线定理,可得.
又注意到,平面EDC,平面EDC,
平面MNQ,,则平面平面.
又平面MQN,则平面.
(2)因平面ABCD,平面ABCD,
则,又,则如图建立以D为原点的空间坐标系.
则.
.
设平面和平面的法向量分别为.
则,取;
,取.
设平面和平面夹角为,则.
则平面和平面夹角的正弦值为.
(3)由(2),设,其中,则
又由题可得,平面的一个法向量可取.
结合直线与平面所成的角为,
则.
则,.
设平面法向量为,则.
取,则点到平面的距离.
19.(1)
(2)112万元
【分析】(1)设出过点的圆的一般方程,代入三个点的坐标,待定系数法求出圆的一般方程,化为标准方程,得到圆心,即建筑物的中心的坐标;
(2)求出,由垂径定理得到点到的距离,从而求出开通的这条路的最低造价.
【详解】(1)由题可知,
由题可知经过点的圆的圆心即为所建建筑物的中心,
设圆的方程为,
则,解得,
圆的方程为,即,
建筑物的中心的坐标为.
(2)因为为建筑物的中心坐标,
设线段EF的中点为Q,由垂径定理得HQ的长度为点H到EF的最小距离,
,圆的半径为,
点到的距离为,
开通的这条路的最低造价为(万元).
20.(1)
(2)
【分析】(1)先由题意表示出,,然后表示出,从而利用基本不等式求出的最大值,进而得到取得最大值时点的位置;
(2)建立平面直角坐标系,从而利用斜率公式表示出,,然后表示出,从而利用基本不等式求出的最大值,进而得到取得最大值时点的位置.
【详解】(1)若选择线路,设,其中,,,
则,,
所以
,
当且仅当时,即当时,等号成立,此时,
由题意知,因为函数在上单调递增,
所以最大时,最大,
所以,若选择线路,则甲带球码时,到达最佳射门位置.
(2)若选择线路,以线段的中点为坐标原点,、的方向分别为、轴的正方向建立如图所示的平面直角坐标系,
则,,,,
则,直线的方程为,
设点,其中,
,,
所以
,
令,则,
所以,
当且仅当,即,即时,等号成立,
所以,
当且仅当时,等号成立,此时,,
由题意知,因为函数在上单调递增,
所以最大时,最大,
所以,若选择线路,则甲带球码时,到达最佳射门位置.
答案第1页,共2页
答案第1页,共2页
