《图形的认识与测量—与面相关的计算》 课件
文档属性
| 名称 | 《图形的认识与测量—与面相关的计算》 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-19 11:59:50 | ||
图片预览






文档简介
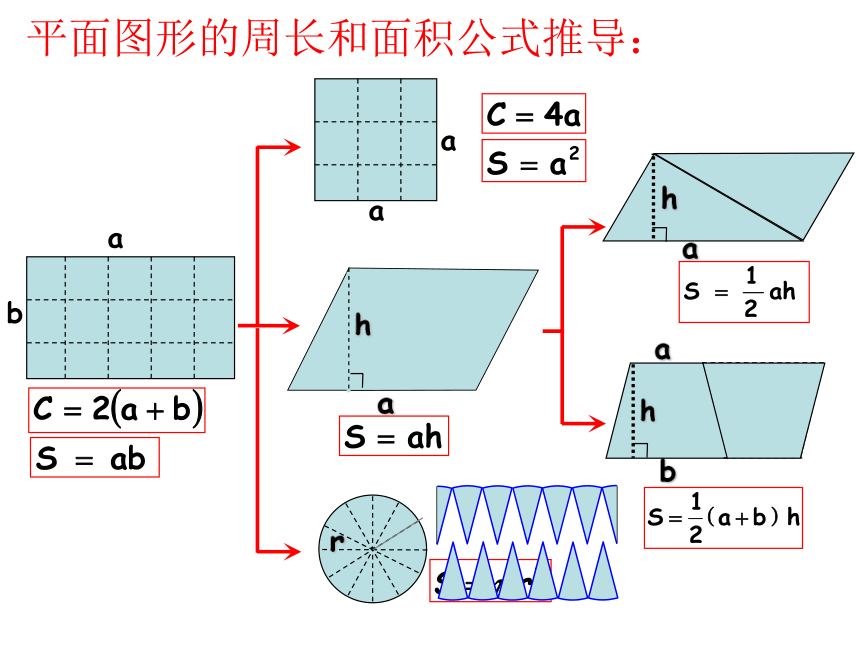
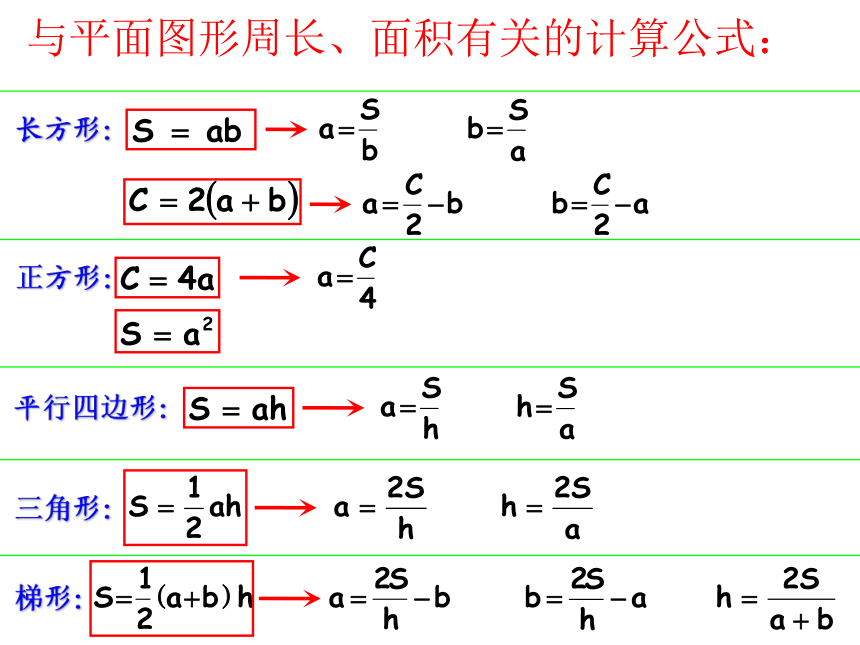
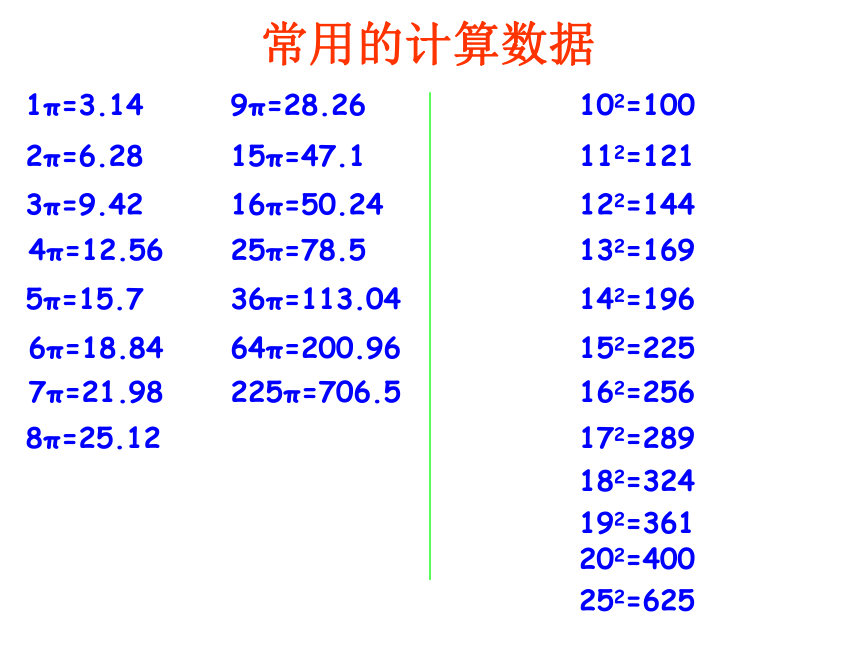
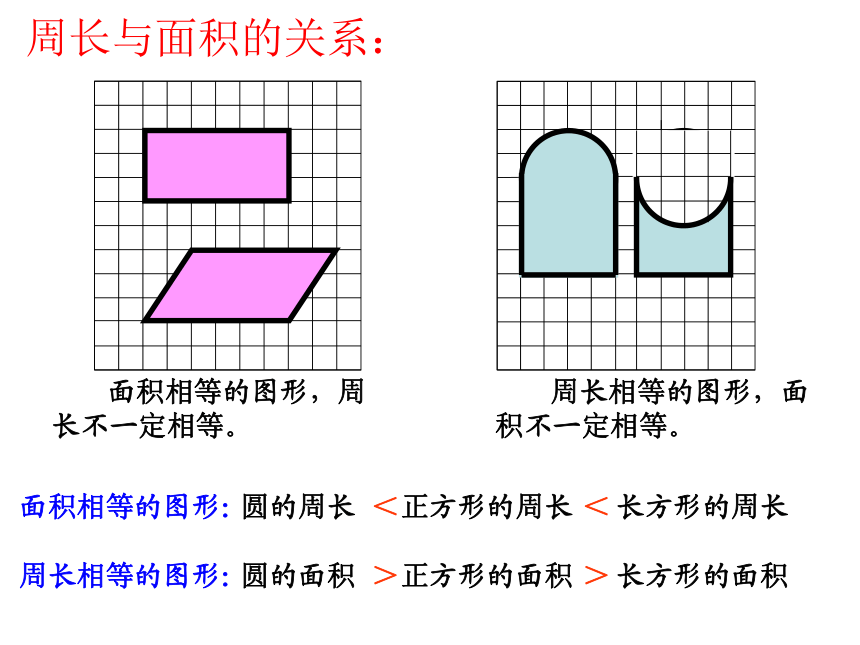
课件39张PPT。小学数学总复习图形的认识与测量二十、与面相关的计算平面图形的周长: 围成平面图形的所有边长的总和,叫做平面图形的周长。平面图形的面积: 物体表面的大小或物体所占平面的大小,叫做面积。abaaahahabhr平面图形的周长和面积公式推导:平行四边形:长方形:三角形:梯形:与平面图形周长、面积有关的计算公式:正方形:r=d÷2r=C÷π÷2d=2rd=C÷πC=2πrC=πdS=πr2S=π(d÷2)2S=π(C÷π÷2)2与圆有关的计算公式圆环面积:S环=πR2 -πr2S环=π(R2 -r2)扇形面积:1π=3.14常用的计算数据2π=6.283π=9.424π=12.565π=15.76π=18.847π=21.988π=25.129π=28.2616π=50.2425π=78.536π=113.0464π=200.9615π=47.1102=100112=121122=144132=169142=196152=225225π=706.5162=256172=289182=324192=361202=400252=625 周长相等的图形,面积不一定相等。周长与面积的关系: 面积相等的图形,周长不一定相等。面积相等的图形:圆的周长<正方形的周长长方形的周长<周长相等的图形:圆的面积>正方形的面积>长方形的面积练习1、面积相等的两个梯形一定可以拼成一个平行四
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )判 断××√××6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小
棒,能围成一个三角形。( )判 断×××√×√××判 断14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是1800。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )××√×√×判 断20、两个半圆一定能拼成一个圆。? ( )
21、半径是2厘米的圆,周长和面积相等( )
22、大圆的圆周率比小圆的圆周率大。 ( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似
长方形,长方形的周长比圆的周长长。 ( )××××√判 断25、在同一个圆内可以画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等。( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )√××√√×1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
6、把圆规的两脚分开,定好两脚间的距离作为( )。
7、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。圆心 O半径直径无数无数 1轴对称半径无数 曲线圆心 填空: 8、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
9、周长相等的圆、正方形和长方形,( )的面积最大。
10、圆中最长的线段是圆的( )。
11、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。不变增加圆直径51.4 填空: 12、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
13、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
14、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
15、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。212.563393:43:49:163:41256 填空: 填空: 16、三角形的一个内角正好等于其余两个内角的和,这是一个(??? )三角形。
17、一个等腰三角形,它的顶角是72o,它的底角是(??? )度。18、6时整,时针与分针组成的角的度数是( )
19、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是(?? )厘米,最少是(??? )厘米。
20、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是(???? )厘米。
21、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是(???? )、(???? )和(???? )厘米。正54180o211826012018022、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角三具有( )的特性,而推拉或防盗门则是由许多小平边四边形组成的,这是应用平行四边形( )的特性。 填空:
23、一个等边三角形,它的每个内角都是( )度,等腰直角三角形的两个底角都是( )度。24、三角形三个角度数的比是2:4:3,最大的角是( )。不易变形容易变形60458025、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
26、一个正方形周长是1.2米,它的面积是( )平方米。
27、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。240.0912 填空: 28、一个平角按4∶5分成两个角。这两个角的度数分别是( ?? )和( ? ?)。
29、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
30、角的两边都是(?? )线。角的大小与(? ?? ?)有关,与( ??)无关。80°100°55射边的长短两边开叉的大小1、画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
2、从圆心到( )任意一点的线段,叫半径。
A.圆心 B.圆外 C.圆上
3、通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线ACB 选择: 4、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
5、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
6、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21ABC 选择: 7、人们常用三角形的(???? )性生产自行车大梁,运用平行四边形的(???? )性制造电动大门。
A.稳定性???? B.易变形?????? C.平衡性
8、平行四边形有(????? )高,梯形有(????? )条高,三角形有(????? )条高。
A.无数条???? B.一条???????? C.三条
9、圆的半径扩大2倍,则它的直径扩大(???? ),面积扩大(????? )。
A.2倍?????? B.4倍????????? C.8倍 选择: ABAABAB10、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
11、一个长方形的长和宽各增加4厘米,它增加的面积是( )平方厘米。
A.等于16平方厘米 B. 小于16平方厘米
C. 大于16平方厘米
12、已知半圆的直径是8厘米,求它的面积。正确列式( )。
A. 3.14×82÷2
B. 3.14×(8÷2)2÷2
C. 3.14×8÷2+8 选择: ACB解决问题1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。3.14×(10÷2)2=3.14×52=3.14×25=78.5(cm2)解决问题2、求右面图形的面积。(单位:厘米)15×8÷2 +(15+25)×10÷2 + 25×9﹦60+200+225﹦485S﹦ah÷2+ (a+b)h÷2 + ah答:它的面积是485平方厘米。解决问题3、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60,求三角形地的高是多少? 【解题思路导引】找出正方形的面积→S正方形=S三角形→三角形的高正方形的边长为:120÷4=30(m)
三角形面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。解决问题4、一块长方形的铁板,长15米,宽是长的 ,要在这块铁板上截一个最大的圆,这个圆的面积是多少平方米?长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。练习十九不经历风雨,
怎能见彩虹。
边形。 ( )
2、面积相等的两个三角形形状也相同。( )
3、同底等高的两个三角形的面积一定相等。( )
4、周长相等的长方形和平行四边形,他们的面积一
定相等。( )
5、底和高都是0.2厘米的三角形的面积是0.2平方
厘米。( )判 断××√××6、平行四边形的底越长,它的面积就越大。( )
7、三角形的面积是平行四边形面积的一半。( )
8、两个三角形的高相等,它们的面积就相等。( )
9、大于90°的角叫钝角。( )
10、角的两条边越长,角就越大。( )
11、钟表的分针旋转一周,时针旋转30°。( )
12、可以画一条长10厘米的直线。( )
13、用3根长度分别是8厘米、12厘米、3厘米的小
棒,能围成一个三角形。( )判 断×××√×√××判 断14、平角就是一条直线。( )
15、任意一个三角形的三个内角的和都是1800。( )
16、任意的三条线段都可以围成一个三角形。( )
17、每个三角形至少有2个锐角。( )
18、有一组对边平行的四边形是梯形。( )
19、两端都在圆上的线段是直径。( )××√×√×判 断20、两个半圆一定能拼成一个圆。? ( )
21、半径是2厘米的圆,周长和面积相等( )
22、大圆的圆周率比小圆的圆周率大。 ( )
23、半圆形纸片的周长就是圆周长的一半。( )
24、把半径3厘米的圆等分成十六份,拼成一个近似
长方形,长方形的周长比圆的周长长。 ( )××××√判 断25、在同一个圆内可以画100条直径。( )
26、所有的圆的直径都相等。( )
27、等圆的半径都相等。( )
28、两端都在圆上的线段叫做直径。( )
29、圆心到圆上任意一点的距离都相等。( )
30、半径是2厘米的圆比直径是3厘米的圆大。( )√××√√×1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
6、把圆规的两脚分开,定好两脚间的距离作为( )。
7、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。圆心 O半径直径无数无数 1轴对称半径无数 曲线圆心 填空: 8、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
9、周长相等的圆、正方形和长方形,( )的面积最大。
10、圆中最长的线段是圆的( )。
11、把一个直径是10厘米的圆剪成两个半圆,则两个半圆周长的和是( )厘米。不变增加圆直径51.4 填空: 12、用圆规画一个周长12.56厘米的圆,圆规两脚之间的距离是( )厘米,所画圆的面积是( )平方厘米。
13、圆的半径扩大3倍,直径扩大( )倍,周长扩大( )倍;面积扩大( )倍。
14、小铁环直径6分米,大铁环直径8分米。小铁环和大铁环半径的比是( );周长的比是( );面积的比是( )。如果它们滚过相同的路程,则转动的圈数的比是( )。
15、在一张长60厘米,宽40厘米的长方形纸上剪一个最大的圆,则圆的面积是( )平方厘米。212.563393:43:49:163:41256 填空: 填空: 16、三角形的一个内角正好等于其余两个内角的和,这是一个(??? )三角形。
17、一个等腰三角形,它的顶角是72o,它的底角是(??? )度。18、6时整,时针与分针组成的角的度数是( )
19、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是(?? )厘米,最少是(??? )厘米。
20、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是(???? )厘米。
21、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是(???? )、(???? )和(???? )厘米。正54180o211826012018022、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角三具有( )的特性,而推拉或防盗门则是由许多小平边四边形组成的,这是应用平行四边形( )的特性。 填空:
23、一个等边三角形,它的每个内角都是( )度,等腰直角三角形的两个底角都是( )度。24、三角形三个角度数的比是2:4:3,最大的角是( )。不易变形容易变形60458025、一个直角三角形的三条边分别长6厘米、8厘米和10厘米。这个三角形的面积是( )平方厘米。
26、一个正方形周长是1.2米,它的面积是( )平方米。
27、一个等腰三角形的两条边分别是2厘米和5厘米,这个等腰三角形的周长是( )厘米。240.0912 填空: 28、一个平角按4∶5分成两个角。这两个角的度数分别是( ?? )和( ? ?)。
29、一个直角三角形的一个锐角是35度,另一个锐角是( )度。
30、角的两边都是(?? )线。角的大小与(? ?? ?)有关,与( ??)无关。80°100°55射边的长短两边开叉的大小1、画圆时,圆规两脚间的距离是( )。
A.半径长度 B.直径长度
2、从圆心到( )任意一点的线段,叫半径。
A.圆心 B.圆外 C.圆上
3、通过圆心并且两端都在圆上的( )叫直径。
A.直线 B.线段 C.射线ACB 选择: 4、周长相等的长方形、正方形和圆中,( )的面积最小。
A、长方形 B、正方形 C、圆
5、把用木条钉成的长方形拉成平行四边形,比较它们的周长和面积。( )
A周长和面积都变化 B、面积变化,周长不变
C、周长变化,面积不变
6、用一根长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是( )平方厘米。
A、6 B、10 C、15 D、21ABC 选择: 7、人们常用三角形的(???? )性生产自行车大梁,运用平行四边形的(???? )性制造电动大门。
A.稳定性???? B.易变形?????? C.平衡性
8、平行四边形有(????? )高,梯形有(????? )条高,三角形有(????? )条高。
A.无数条???? B.一条???????? C.三条
9、圆的半径扩大2倍,则它的直径扩大(???? ),面积扩大(????? )。
A.2倍?????? B.4倍????????? C.8倍 选择: ABAABAB10、一个平行四边形和一个三角形等底等高,已知平行四边形的面积是25平方厘米,三角形的面积是( )平方厘米。
A. 12.5 B. 25 C. 50
11、一个长方形的长和宽各增加4厘米,它增加的面积是( )平方厘米。
A.等于16平方厘米 B. 小于16平方厘米
C. 大于16平方厘米
12、已知半圆的直径是8厘米,求它的面积。正确列式( )。
A. 3.14×82÷2
B. 3.14×(8÷2)2÷2
C. 3.14×8÷2+8 选择: ACB解决问题1、把一个圆分割拼成一个近似的长方形,长方形的周长比圆的周长多10厘米,求圆的面积。3.14×(10÷2)2=3.14×52=3.14×25=78.5(cm2)解决问题2、求右面图形的面积。(单位:厘米)15×8÷2 +(15+25)×10÷2 + 25×9﹦60+200+225﹦485S﹦ah÷2+ (a+b)h÷2 + ah答:它的面积是485平方厘米。解决问题3、一块周长为120米的正方形地与一块三角形地的面积相等,三角形地的底为60,求三角形地的高是多少? 【解题思路导引】找出正方形的面积→S正方形=S三角形→三角形的高正方形的边长为:120÷4=30(m)
三角形面积为:30×30=900 (m2)
三角形的高为:900×2÷60=30(m)
答:三角形地的高为30米。解决问题4、一块长方形的铁板,长15米,宽是长的 ,要在这块铁板上截一个最大的圆,这个圆的面积是多少平方米?长方形的宽为:
圆的半径为:10÷2=5(m)
圆的面积为:52×3.14=78.5(m2)
答:圆的面积是78.5平方米。练习十九不经历风雨,
怎能见彩虹。
