14.1.2 幂的乘方 课件(共21张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 14.1.2 幂的乘方 课件(共21张PPT)【2023秋人教八上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 22:33:30 | ||
图片预览








文档简介
(共21张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十四章 整式的乘法与因式分解
14.1.2 幂的乘方
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解并掌握幂的乘方法则.
2.会运用幂的乘方法则进行运算.
学习目标
重点
难点
通过上节课的学习,你知道怎样做同底数幂的乘法?
(m、n为正整数).
同底数幂相乘,底数不变,指数相加.
新课引入
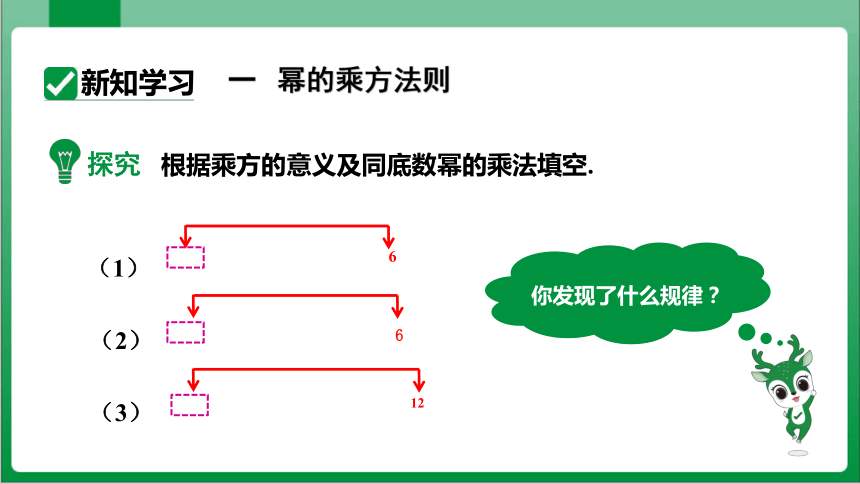
一 幂的乘方法则
探究
根据乘方的意义及同底数幂的乘法填空.
6
12
6
(1)
(2)
(3)
你发现了什么规律?
新知学习
猜想:(am)n=_____.
amn
证一证:
(am)n
n个am
n个m
你们真棒,你的猜想是正确的!
幂的乘方法则
(am)n= amn (m,n都是正整数)
即幂的乘方,底数______,指数 .
不变
相乘
归纳
例1 计算:
(1)(103)5 ;
解: (1) (103)5 = 103×5 = 1015;
(2) (a4)4 = a4×4 = a16;
(3) (am)2 =am×2=a2m;
(3)(am)2;
(2)(a4)4;
(4)-(x4)3.
(4) -(x4)3 =-x4×3=-x12.
思考
(-a5)2表示2个-a5相乘,结果没有负号.
(-a2)5和(-a5)2的结果相同吗 为什么
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
问题1
问题2 下面这道题该怎么进行计算呢?
思考
幂的乘方:
=(a10)3
=a30
底数不变
指数相乘
指数相加
同底数幂
的乘法
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
思考
例3 已知5m = 3,5n = 2,求下列各式的值.
(1)53m; (2)52n; (3)53m + 2n.
解:(1)53m = (5m)3 = 33 = 27;
(2)52n = (5n)2 = 22 = 4;
(3)53m+2n = 53m×52n = 27×4 = 108.
方法总结:此类题的关键是逆用幂的乘方及同底数幂的乘法法则,将所求代数式正确变形,然后代入已知条件求值即可.
1.判断下面计算是否正确?正确的说出理由,不正确的请改正.
(1)(x3)3=x6
原式=x3×3=x9
×
(2)x3. x3=x9
×
原式=x3+3=x6
(3)x3+ x3=x9
×
原式=2x3
针对训练
2.计算:
(1)(103) 3; (2) (x3)2;
(3) -(xm)5; (4) (a2) 3 a 5.
解:(1)(103) 3=109 ;
(2) (x3)2 =x6 ;
(3) -(xm)5=-x5m ;
(4) (a2) 3 a 5 =a 6 a 5=a11.
2.若xm x2m = 3,求x9m的值.
解:∵xm·x2m =x3m = 3,
∴x9m = (x3m)3 = 33 = 27.
1.计算.
[(x3)2]2=______=________
[(y4)m]n=______=________
(x6)2
x12
(y4m)n
y4mn
随堂练习
3.已知 am=3,an=5,
求:(1)a2m ,a3n的值;
解: a2m+3n= a2m·a3n=9×125 =1125.
(3) a2m+3n 的值.
(2) am+n 的值.
解: am+n= am·an=3×5=15;
解: a2m= (am)2= 32 = 9,
a3n= (an)3= 53= 125;
4.地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是
地球的10倍和102倍,它们的体积分别约是地球的多少倍?
分析:球的体积公式是V= r3,其中V是球的体积,r是球的半径.所以
球的体积之比经过化简之后就等于半径之比.
解:木星的半径是地球的10倍,它的体积是地球的103倍;
太阳的半径是地球的102倍,它的体积是地球的(102)3=106倍.
注意
法则
幂的乘方
幂的乘方,底数不变,指数相乘
(am)n=amn (m,n都是正整数)
幂的乘方与同底数幂的乘法的区别:
(am)n=amn; am·an=am+n
幂的乘方法则的逆用:
amn=(am)n=(an)m
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十四章 整式的乘法与因式分解
14.1.2 幂的乘方
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解并掌握幂的乘方法则.
2.会运用幂的乘方法则进行运算.
学习目标
重点
难点
通过上节课的学习,你知道怎样做同底数幂的乘法?
(m、n为正整数).
同底数幂相乘,底数不变,指数相加.
新课引入
一 幂的乘方法则
探究
根据乘方的意义及同底数幂的乘法填空.
6
12
6
(1)
(2)
(3)
你发现了什么规律?
新知学习
猜想:(am)n=_____.
amn
证一证:
(am)n
n个am
n个m
你们真棒,你的猜想是正确的!
幂的乘方法则
(am)n= amn (m,n都是正整数)
即幂的乘方,底数______,指数 .
不变
相乘
归纳
例1 计算:
(1)(103)5 ;
解: (1) (103)5 = 103×5 = 1015;
(2) (a4)4 = a4×4 = a16;
(3) (am)2 =am×2=a2m;
(3)(am)2;
(2)(a4)4;
(4)-(x4)3.
(4) -(x4)3 =-x4×3=-x12.
思考
(-a5)2表示2个-a5相乘,结果没有负号.
(-a2)5和(-a5)2的结果相同吗 为什么
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
问题1
问题2 下面这道题该怎么进行计算呢?
思考
幂的乘方:
=(a10)3
=a30
底数不变
指数相乘
指数相加
同底数幂
的乘法
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
思考
例3 已知5m = 3,5n = 2,求下列各式的值.
(1)53m; (2)52n; (3)53m + 2n.
解:(1)53m = (5m)3 = 33 = 27;
(2)52n = (5n)2 = 22 = 4;
(3)53m+2n = 53m×52n = 27×4 = 108.
方法总结:此类题的关键是逆用幂的乘方及同底数幂的乘法法则,将所求代数式正确变形,然后代入已知条件求值即可.
1.判断下面计算是否正确?正确的说出理由,不正确的请改正.
(1)(x3)3=x6
原式=x3×3=x9
×
(2)x3. x3=x9
×
原式=x3+3=x6
(3)x3+ x3=x9
×
原式=2x3
针对训练
2.计算:
(1)(103) 3; (2) (x3)2;
(3) -(xm)5; (4) (a2) 3 a 5.
解:(1)(103) 3=109 ;
(2) (x3)2 =x6 ;
(3) -(xm)5=-x5m ;
(4) (a2) 3 a 5 =a 6 a 5=a11.
2.若xm x2m = 3,求x9m的值.
解:∵xm·x2m =x3m = 3,
∴x9m = (x3m)3 = 33 = 27.
1.计算.
[(x3)2]2=______=________
[(y4)m]n=______=________
(x6)2
x12
(y4m)n
y4mn
随堂练习
3.已知 am=3,an=5,
求:(1)a2m ,a3n的值;
解: a2m+3n= a2m·a3n=9×125 =1125.
(3) a2m+3n 的值.
(2) am+n 的值.
解: am+n= am·an=3×5=15;
解: a2m= (am)2= 32 = 9,
a3n= (an)3= 53= 125;
4.地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是
地球的10倍和102倍,它们的体积分别约是地球的多少倍?
分析:球的体积公式是V= r3,其中V是球的体积,r是球的半径.所以
球的体积之比经过化简之后就等于半径之比.
解:木星的半径是地球的10倍,它的体积是地球的103倍;
太阳的半径是地球的102倍,它的体积是地球的(102)3=106倍.
注意
法则
幂的乘方
幂的乘方,底数不变,指数相乘
(am)n=amn (m,n都是正整数)
幂的乘方与同底数幂的乘法的区别:
(am)n=amn; am·an=am+n
幂的乘方法则的逆用:
amn=(am)n=(an)m
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
