空间直角坐标系
图片预览



文档简介
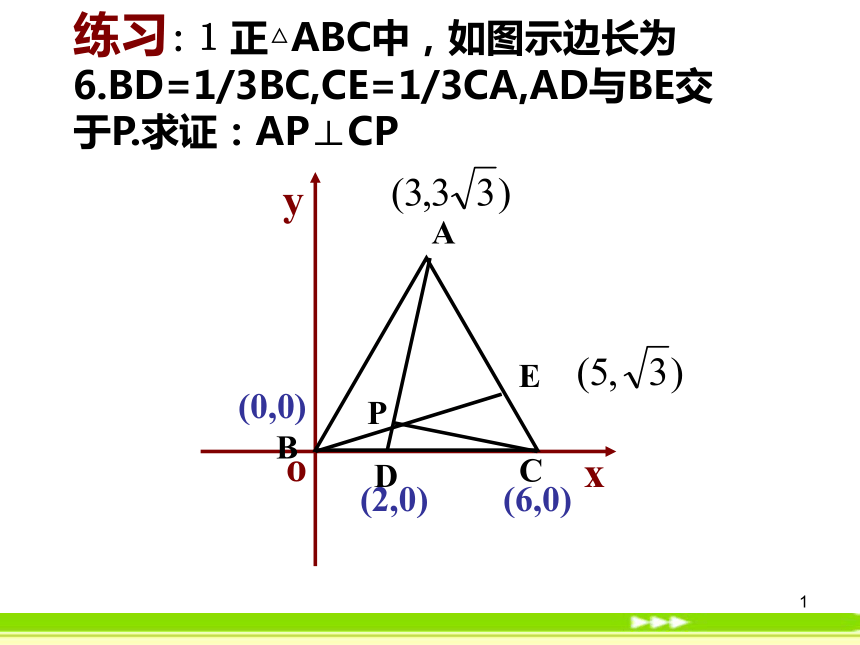
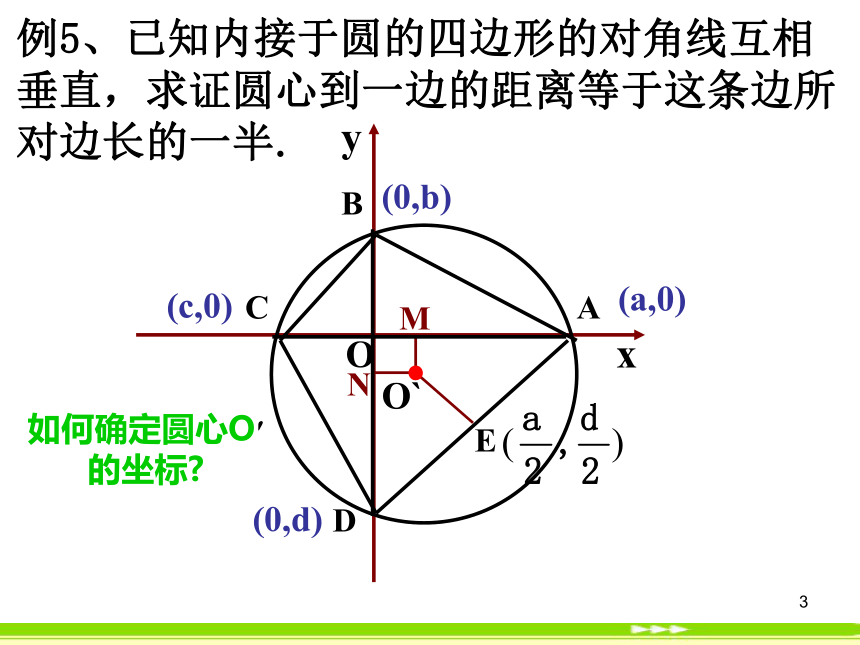
课件24张PPT。1练习:1正△ABC中,如图示边长为6.BD=1/3BC,CE=1/3CA,AD与BE交于P.求证:AP⊥CP(6,0)(2,0)(0,0)2用坐标法解决平面几何问题的步骤:第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.3E例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)如何确定圆心O′
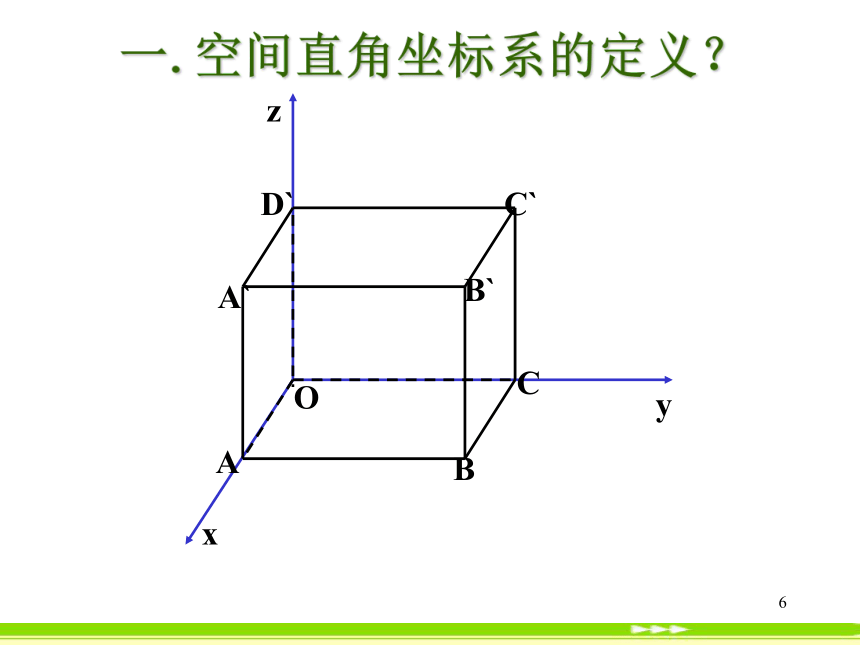
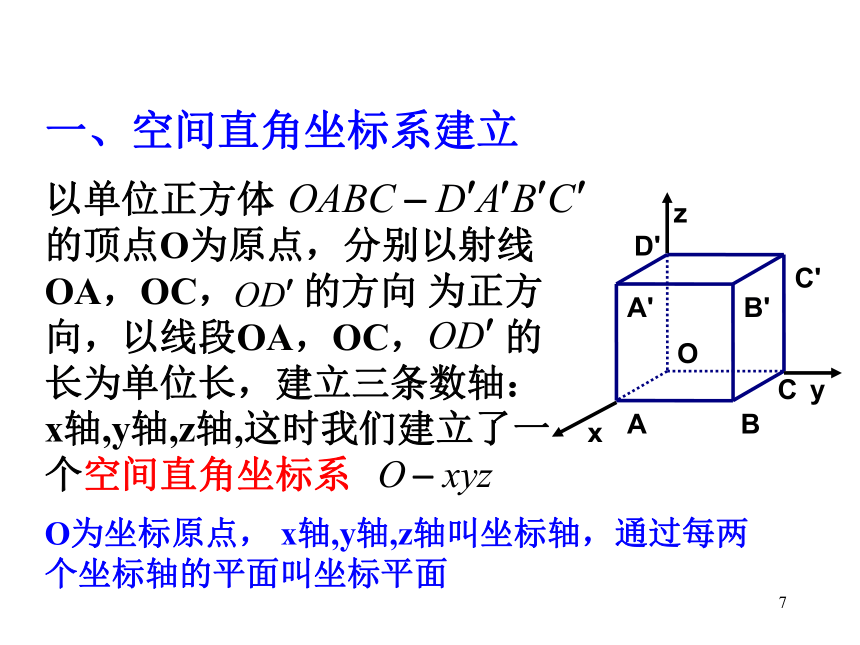
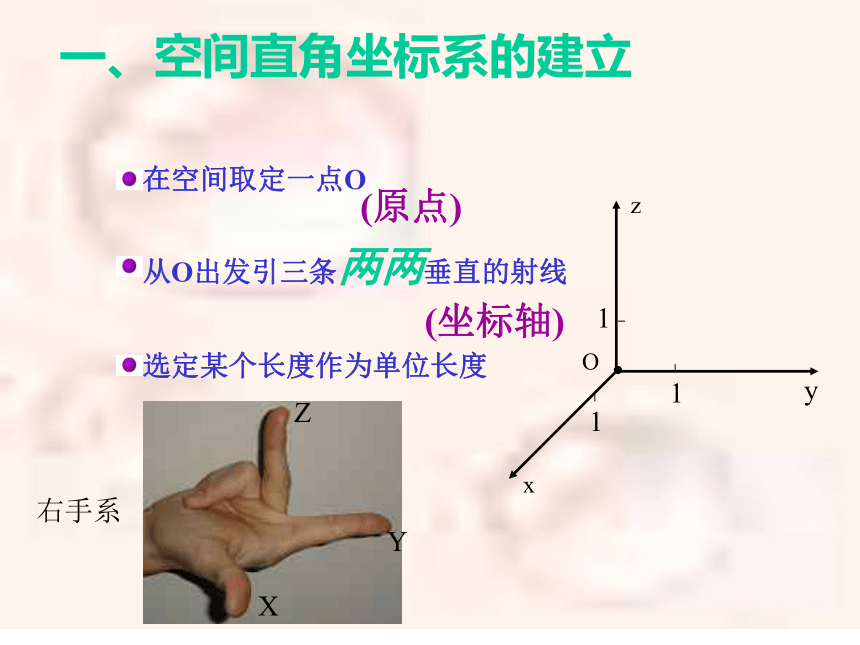
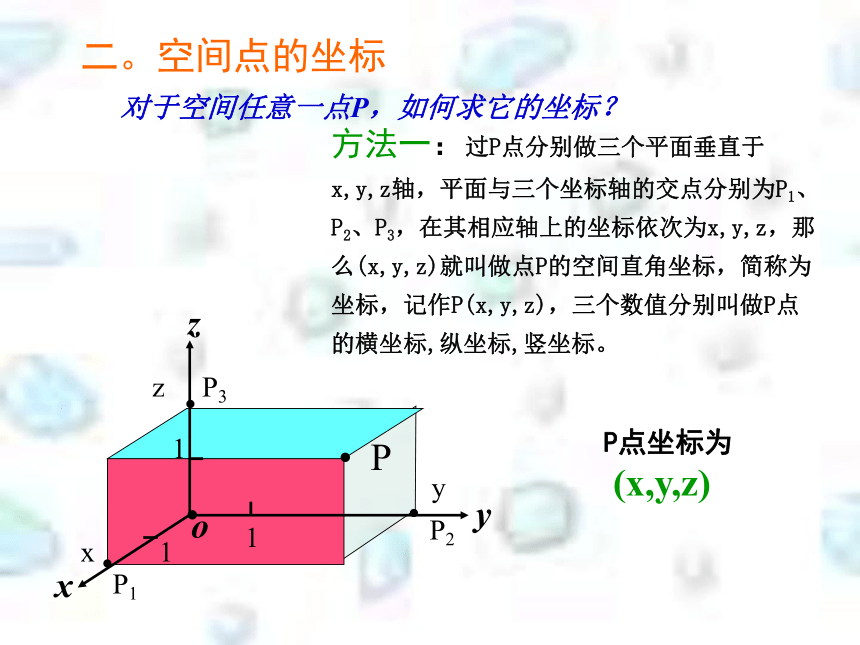
的坐标?4§4.3.1 空间直角坐标系 数学组-----郝56一.空间直角坐标系的定义?7一、空间直角坐标系建立以单位正方体 的顶点O为原点,分别以射线OA,OC, 的方向 为正方向,以线段OA,OC, 的长为单位长,建立三条数轴:x轴,y轴,z轴,这时我们建立了一个空间直角坐标系BO为坐标原点, x轴,y轴,z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面8一、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的射线选定某个长度作为单位长度(原点)(坐标轴)?Oxyz111右手系9?P1P2P3yxz??二。空间点的坐标对于空间任意一点P,如何求它的坐标?方法一:过P点分别做三个平面垂直于x,y,z轴,平面与三个坐标轴的交点分别为P1、P2、P3,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值分别叫做P点的横坐标,纵坐标,竖坐标。P点坐标为
(x,y,z)10如图:空间直角坐标系中的棱长为1的正方体
说出各点的坐标.分析:先定x 、y
再定z.E11??P0xyz方法二:过P点作xoy面的垂线,垂足为P0点。点P0在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足P1在z轴上的坐标z就是P点的竖坐标。P点坐标为
(x,y,z)P112例题1、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点C,B`,P的坐标.OBA`B`C`PP`13练习QQ`1、如图,棱长为a的正方体OABC-D`A`B`C`中,对角线OB`于BD`相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴的正半轴上.试写出点Q的坐标.14结晶体的基本单位称为晶胞,如图是食盐晶胞示意图(可看成是八个棱长为1/2的小正方体堆积成的正方体),其中红色点代表钠原子,黑点代表氯原子,如图:建立空间直角
坐标系 后,
试写出全部钠原子
所在位置的坐标。例3:15三.已知坐标确定点的空间位置空间坐标:用一个三元数组(x,y,z)
表示 x—横坐标,y—纵坐标,z—竖坐标方法:先定x、y,再定z16O例如在空间直角坐标系中标出点:
A (2,3,4)234D`A17?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C例2、在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);18练一练在空间直角坐标系中描出下列各点,并指出各点所在的位置:
A(0,3,1), B(0,0,5), C(0,3,0)在空间直角坐标系中作出下列各点:
(1)、( -1,-4,1 );
(2)、 ( -3,3,4 );19小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标20归纳:1、原点坐标(0,0,0)
2、在x轴上的点(a,0,0)
3、在y轴上的点(0,b,0)
4、在z轴上的点(0,0,c)
5、在xOy平面内的点(a,b,0)
6、在yOz平面内的点(0,b,c)
7、在xOz平面内的点(a,0,c)练习:点P在z轴的上且到原点的距离是3,则P的坐标是___________不见的那个就为“0”21四.对称问题在空间直角坐标系中,点M(1,-2,3)1)关于xoy平面的对称点是M/( )2)关于yoz平面的对称点是M/( )3)关于xoz平面的对称点是M/( )4)关于x轴的对称点是M/( )5)关于y轴的对称点是M/( )6)关于z轴的对称点是M/( )7)关于原点的对称点是M/( )不见哪个,就变那个2019/3/1422若r为常数,那么x2+y2+z2=r2表示以(0,0,0)为球心的球面2019/3/1423M2xyzoM1N1N2NMP1P2H设P1(x1,y1,z1),P2(x2,y2,z2)则M,N的坐标为M(x1,y1,0)
N(x2,y2,0)2019/3/1424求距离1. A(1,0,2) B(3,1,4)
2. A(6,0,1)B(3,5,7)
3.在z轴上求一点M,使得M点到
A(1,0,2)与点B(1,-3,1) 的距离相等。
的坐标?4§4.3.1 空间直角坐标系 数学组-----郝56一.空间直角坐标系的定义?7一、空间直角坐标系建立以单位正方体 的顶点O为原点,分别以射线OA,OC, 的方向 为正方向,以线段OA,OC, 的长为单位长,建立三条数轴:x轴,y轴,z轴,这时我们建立了一个空间直角坐标系BO为坐标原点, x轴,y轴,z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面8一、空间直角坐标系的建立在空间取定一点O从O出发引三条两两垂直的射线选定某个长度作为单位长度(原点)(坐标轴)?Oxyz111右手系9?P1P2P3yxz??二。空间点的坐标对于空间任意一点P,如何求它的坐标?方法一:过P点分别做三个平面垂直于x,y,z轴,平面与三个坐标轴的交点分别为P1、P2、P3,在其相应轴上的坐标依次为x,y,z,那么(x,y,z)就叫做点P的空间直角坐标,简称为坐标,记作P(x,y,z),三个数值分别叫做P点的横坐标,纵坐标,竖坐标。P点坐标为
(x,y,z)10如图:空间直角坐标系中的棱长为1的正方体
说出各点的坐标.分析:先定x 、y
再定z.E11??P0xyz方法二:过P点作xoy面的垂线,垂足为P0点。点P0在坐标系xOy中的坐标x、y依次是P点的横坐标、纵坐标。再过P点作z轴的垂线,垂足P1在z轴上的坐标z就是P点的竖坐标。P点坐标为
(x,y,z)P112例题1、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=3,A`C`于B`D`相交于点P.分别写出点C,B`,P的坐标.OBA`B`C`PP`13练习QQ`1、如图,棱长为a的正方体OABC-D`A`B`C`中,对角线OB`于BD`相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴的正半轴上.试写出点Q的坐标.14结晶体的基本单位称为晶胞,如图是食盐晶胞示意图(可看成是八个棱长为1/2的小正方体堆积成的正方体),其中红色点代表钠原子,黑点代表氯原子,如图:建立空间直角
坐标系 后,
试写出全部钠原子
所在位置的坐标。例3:15三.已知坐标确定点的空间位置空间坐标:用一个三元数组(x,y,z)
表示 x—横坐标,y—纵坐标,z—竖坐标方法:先定x、y,再定z16O例如在空间直角坐标系中标出点:
A (2,3,4)234D`A17?A1(1,4,0)?A(1,4,1)?(2,-2,0)
B1? B
(2,-2,-1)?(-1,-3,0)
C1?(-1,-3,3)
C例2、在空间直角坐标系中作出下列各点
(1)、A(1,4,1);
(2)、B(2,-2,-1);
(3)、C(-1,-3,3);18练一练在空间直角坐标系中描出下列各点,并指出各点所在的位置:
A(0,3,1), B(0,0,5), C(0,3,0)在空间直角坐标系中作出下列各点:
(1)、( -1,-4,1 );
(2)、 ( -3,3,4 );19小提示:坐标轴上的点至少有两个坐标等于0;坐标面上的点至少有一个坐标等于0。(0,0,0)(x,0,0)(0,y,0)(0,0,z)(x,y,0)(0,y,z)(x,0,z)4、特殊位置的点的坐标20归纳:1、原点坐标(0,0,0)
2、在x轴上的点(a,0,0)
3、在y轴上的点(0,b,0)
4、在z轴上的点(0,0,c)
5、在xOy平面内的点(a,b,0)
6、在yOz平面内的点(0,b,c)
7、在xOz平面内的点(a,0,c)练习:点P在z轴的上且到原点的距离是3,则P的坐标是___________不见的那个就为“0”21四.对称问题在空间直角坐标系中,点M(1,-2,3)1)关于xoy平面的对称点是M/( )2)关于yoz平面的对称点是M/( )3)关于xoz平面的对称点是M/( )4)关于x轴的对称点是M/( )5)关于y轴的对称点是M/( )6)关于z轴的对称点是M/( )7)关于原点的对称点是M/( )不见哪个,就变那个2019/3/1422若r为常数,那么x2+y2+z2=r2表示以(0,0,0)为球心的球面2019/3/1423M2xyzoM1N1N2NMP1P2H设P1(x1,y1,z1),P2(x2,y2,z2)则M,N的坐标为M(x1,y1,0)
N(x2,y2,0)2019/3/1424求距离1. A(1,0,2) B(3,1,4)
2. A(6,0,1)B(3,5,7)
3.在z轴上求一点M,使得M点到
A(1,0,2)与点B(1,-3,1) 的距离相等。
