人教版七年级数学下册7.1.2 平面直角坐标系课件(共16张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.1.2 平面直角坐标系课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 461.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 13:45:10 | ||
图片预览


文档简介
(共16张PPT)
第七章 平面直角坐标系
7.1.2 平面直角坐标系
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念;(重点)
2.能在给定的直角坐标系中,由点的位置写出它的坐标.(难点)
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
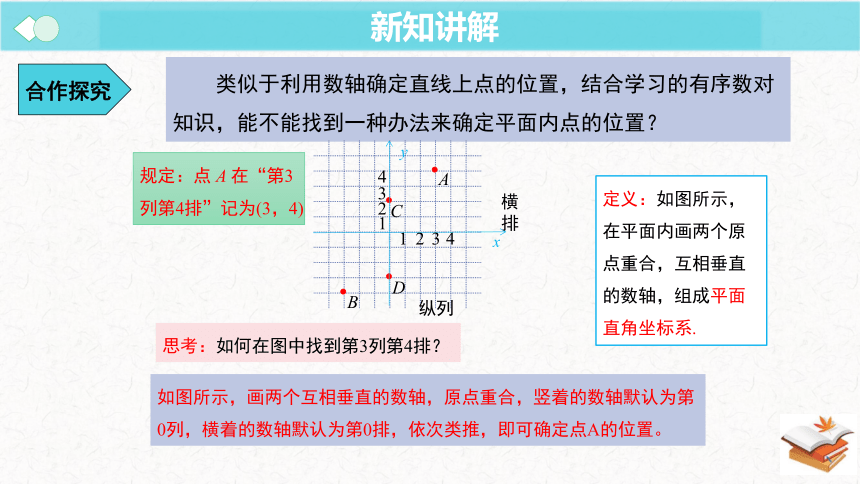
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
B
A
D
C
横
排
纵列
4
3
2
1
3
2
4
1
规定:点 A 在“第3列第4排”记为(3,4)
x
y
思考:如何在图中找到第3列第4排?
如图所示,画两个互相垂直的数轴,原点重合,竖着的数轴默认为第0列,横着的数轴默认为第0排,依次类推,即可确定点A的位置。
定义:如图所示,在平面内画两个原点重合,互相垂直的数轴,组成平面直角坐标系.
合作探究
新知讲解
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x 轴
x
y 轴
y
原点
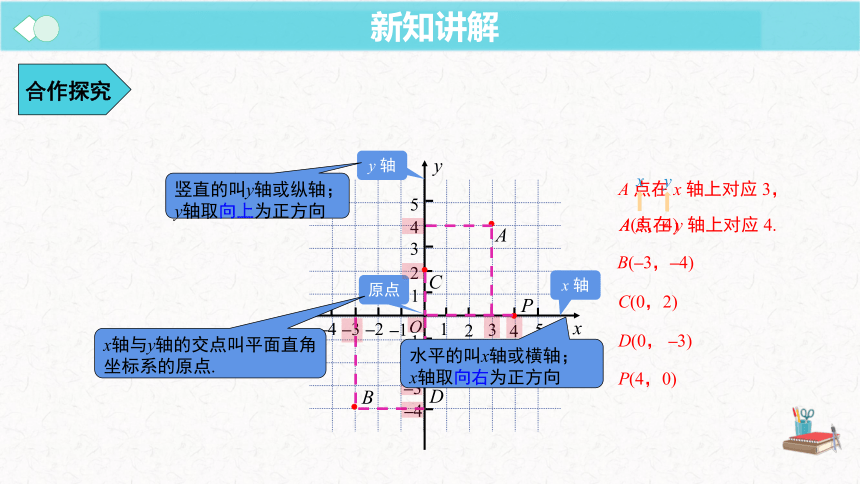
A 点在 x 轴上对应 3,
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
P
P(4,0)
A 点在 y 轴上对应 4.
x
y
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
合作探究
新知讲解
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x
y
(3,4)
(–3,–4)
(0,2)
(0, –3)
P
(4,0)
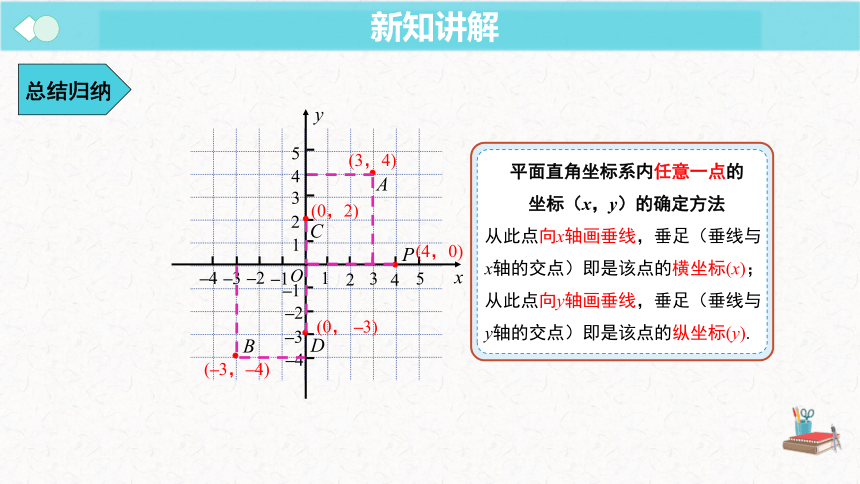
平面直角坐标系内任意一点的
坐标(x,y)的确定方法
从此点向x轴画垂线,垂足(垂线与x轴的交点)即是该点的横坐标(x);
从此点向y轴画垂线,垂足(垂线与y轴的交点)即是该点的纵坐标(y).
总结归纳
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
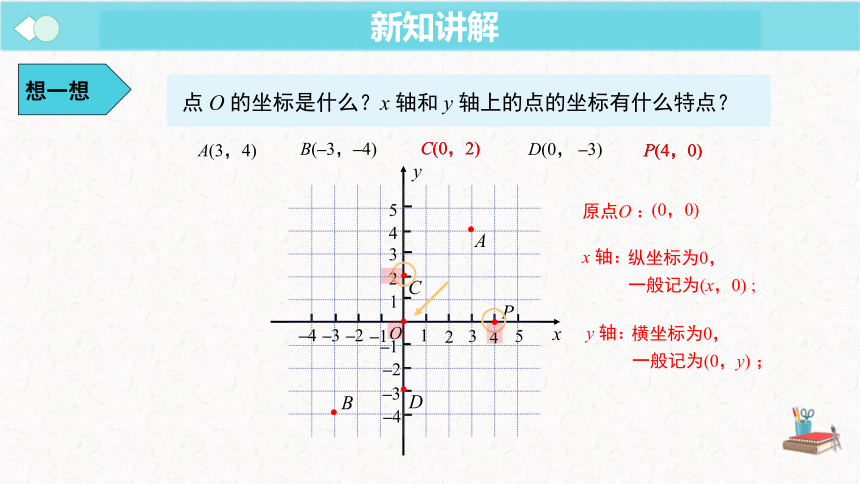
点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
A
B
D
C
x
y
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
原点O :
y 轴:
横坐标为0,
一般记为(0,y) ;
x 轴:
纵坐标为0,
一般记为(x,0) ;
C(0,2)
P(4,0)
P(4,0)
P
(0,0)
想一想
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
x
y
x 轴
y 轴
原点
第一象限
Ⅰ
第二象限
Ⅱ
第三象限
Ⅲ
第四象限
Ⅳ
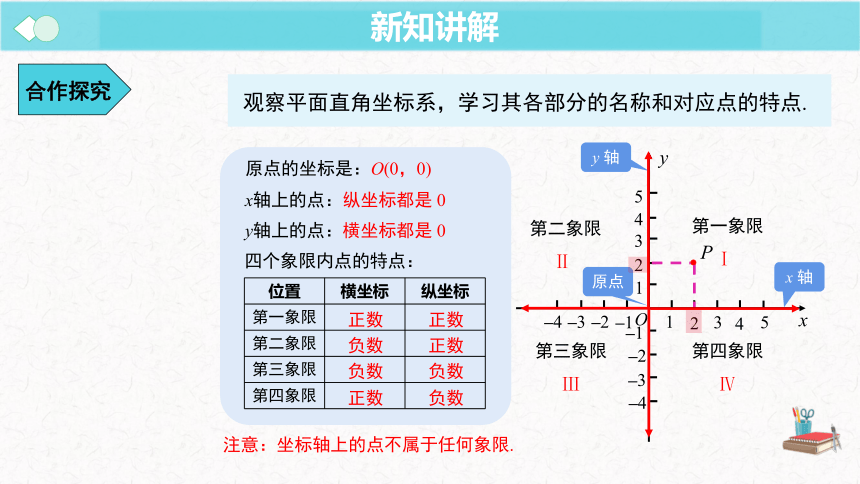
观察平面直角坐标系,学习其各部分的名称和对应点的特点.
P
原点的坐标是:O(0,0)
x轴上的点:纵坐标都是 0
y轴上的点:横坐标都是 0
四个象限内点的特点:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
注意:坐标轴上的点不属于任何象限.
合作探究
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
在平面直角坐标系中描出下列各点:
y
A
B
C
D
E
平面上的点和坐标有什么关系呢?
平面上的点和坐标是一一对应的.
x
A(4,4),
B(–3,3),
C(–4,–2),
D(3.5,–2),
E(0,–3).
做一做
新知讲解
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么 y 轴是哪条线?
x
C
B
A
D
请你写出正方形的顶点 A,B,C,D 的坐标.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
试着再建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
合作探究
新知讲解
例1.在平面直角坐标系中描出下列各点:
A(4,5) ,B(–2,3) ,C(–4,–1) ,D(2.5,–2) ,E(0,–4) .
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
A
B
C
D
E
x
y
典型例题
新知讲解
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
1.写出图中点 A,B,C,D,E,F 的坐标.
E
C
A
F
B
D
A(–2,–2)
B(–5,4)
C(5,–4)
D(0,–3)
E(2,5)
F(–4,0)
课堂练习
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
2.在图中描出下列各点:
L
L(–5,–3) ,M(4,0) ,N(–6,2) ,P(5,–3.5) ,Q(0,5) ,R(6,2) .
M
N
P
Q
R
课堂练习
3.(1) 下列各点中,在第二象限的是( )
A.(2,3) B.(2,–3)
C.(–2,–3) D.(– 2,3)
(2) 下列各点中,在 x 轴上的点是( )
A.(0,3) B.(–3,0)
C.(–1,2) D.(–2,–3)
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
D
B
x轴上的点:纵坐标都是 0;
课堂练习
4.(1) 若 |a| = 5,|b| = 4,且点 M(a,b) 在第二象限,则点 M 的
坐标是 .
(–5,4)
(2) 已知坐标平面内点 A(a,b) 在第四象限,那么点 B(b,a)
在第 象限,点 C(–a,–b) 在第 象限.
二
二
分析:由点 M 在第二象限得,a<0,b>0.又知道 |a| = 5,|b| = 4,所以 a = –5,b = 4.
分析:由点 A 在第四象限得,a>0,b<0,所以 –a<0,–b>0.所以点B(b,a) 在第二象限,点C(–a,–b) 也在第二象限.
课堂练面直角坐标系
概念:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
点的坐标特点:
原点坐标为(0,0) ,x 轴上的点纵坐标为0,
y 轴上的点横坐标为0,坐标轴上的点不在
任何象限内.
课堂小结
教科书第69页练习7.1
第3、4题
布置作业
第七章 平面直角坐标系
7.1.2 平面直角坐标系
学习目标
1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念;(重点)
2.能在给定的直角坐标系中,由点的位置写出它的坐标.(难点)
3.理解在平面直角坐标系中四个象限的点对应坐标的符号特征.
4.能运用点的坐标的符号特征解决问题,进一步体会数形结合思想的作用.
类似于利用数轴确定直线上点的位置,结合学习的有序数对知识,能不能找到一种办法来确定平面内点的位置?
B
A
D
C
横
排
纵列
4
3
2
1
3
2
4
1
规定:点 A 在“第3列第4排”记为(3,4)
x
y
思考:如何在图中找到第3列第4排?
如图所示,画两个互相垂直的数轴,原点重合,竖着的数轴默认为第0列,横着的数轴默认为第0排,依次类推,即可确定点A的位置。
定义:如图所示,在平面内画两个原点重合,互相垂直的数轴,组成平面直角坐标系.
合作探究
新知讲解
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x 轴
x
y 轴
y
原点
A 点在 x 轴上对应 3,
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
P
P(4,0)
A 点在 y 轴上对应 4.
x
y
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
合作探究
新知讲解
A
B
D
C
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
4
3
2
1
5
–4
x
y
(3,4)
(–3,–4)
(0,2)
(0, –3)
P
(4,0)
平面直角坐标系内任意一点的
坐标(x,y)的确定方法
从此点向x轴画垂线,垂足(垂线与x轴的交点)即是该点的横坐标(x);
从此点向y轴画垂线,垂足(垂线与y轴的交点)即是该点的纵坐标(y).
总结归纳
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
点 O 的坐标是什么?x 轴和 y 轴上的点的坐标有什么特点?
A
B
D
C
x
y
A(3,4)
B(–3,–4)
C(0,2)
D(0, –3)
原点O :
y 轴:
横坐标为0,
一般记为(0,y) ;
x 轴:
纵坐标为0,
一般记为(x,0) ;
C(0,2)
P(4,0)
P(4,0)
P
(0,0)
想一想
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
x
y
x 轴
y 轴
原点
第一象限
Ⅰ
第二象限
Ⅱ
第三象限
Ⅲ
第四象限
Ⅳ
观察平面直角坐标系,学习其各部分的名称和对应点的特点.
P
原点的坐标是:O(0,0)
x轴上的点:纵坐标都是 0
y轴上的点:横坐标都是 0
四个象限内点的特点:
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
注意:坐标轴上的点不属于任何象限.
合作探究
新知讲解
–1
–2
–3
4
3
2
1
5
–4
O
–4
–3
–2
–1
1
2
3
4
5
在平面直角坐标系中描出下列各点:
y
A
B
C
D
E
平面上的点和坐标有什么关系呢?
平面上的点和坐标是一一对应的.
x
A(4,4),
B(–3,3),
C(–4,–2),
D(3.5,–2),
E(0,–3).
做一做
新知讲解
如图,正方形 ABCD 的边长为 6,如果以点 A 为原点,AB 所在直线为 x 轴,建立平面直角坐标系,那么 y 轴是哪条线?
x
C
B
A
D
请你写出正方形的顶点 A,B,C,D 的坐标.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
试着再建立一个平面直角坐标系,这时正方形的顶点 A,B,C,D 的坐标又分别是什么?
y
合作探究
新知讲解
例1.在平面直角坐标系中描出下列各点:
A(4,5) ,B(–2,3) ,C(–4,–1) ,D(2.5,–2) ,E(0,–4) .
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
A
B
C
D
E
x
y
典型例题
新知讲解
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
1.写出图中点 A,B,C,D,E,F 的坐标.
E
C
A
F
B
D
A(–2,–2)
B(–5,4)
C(5,–4)
D(0,–3)
E(2,5)
F(–4,0)
课堂练习
O
–4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
4
3
2
1
5
6
7
–5
–6
x
y
2.在图中描出下列各点:
L
L(–5,–3) ,M(4,0) ,N(–6,2) ,P(5,–3.5) ,Q(0,5) ,R(6,2) .
M
N
P
Q
R
课堂练习
3.(1) 下列各点中,在第二象限的是( )
A.(2,3) B.(2,–3)
C.(–2,–3) D.(– 2,3)
(2) 下列各点中,在 x 轴上的点是( )
A.(0,3) B.(–3,0)
C.(–1,2) D.(–2,–3)
位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
正数
正数
负数
正数
负数
负数
正数
负数
D
B
x轴上的点:纵坐标都是 0;
课堂练习
4.(1) 若 |a| = 5,|b| = 4,且点 M(a,b) 在第二象限,则点 M 的
坐标是 .
(–5,4)
(2) 已知坐标平面内点 A(a,b) 在第四象限,那么点 B(b,a)
在第 象限,点 C(–a,–b) 在第 象限.
二
二
分析:由点 M 在第二象限得,a<0,b>0.又知道 |a| = 5,|b| = 4,所以 a = –5,b = 4.
分析:由点 A 在第四象限得,a>0,b<0,所以 –a<0,–b>0.所以点B(b,a) 在第二象限,点C(–a,–b) 也在第二象限.
课堂练面直角坐标系
概念:
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
点的坐标特点:
原点坐标为(0,0) ,x 轴上的点纵坐标为0,
y 轴上的点横坐标为0,坐标轴上的点不在
任何象限内.
课堂小结
教科书第69页练习7.1
第3、4题
布置作业
