数学人教A版(2019)选择性必修第一册 3.1.1椭圆及其标准方程 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册 3.1.1椭圆及其标准方程 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 23:04:59 | ||
图片预览





文档简介
(共18张PPT)
问题1 用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆. 如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢?
椭圆
抛物线
双曲线
圆
我们通常把椭圆、抛物线、双曲线统称为圆锥曲线
生产、生活中的圆锥曲线
行星绕太阳运行的轨道(椭圆)
发电厂冷却塔的外形线(双曲线)
卫星接收天线(抛物线)
生产、生活中的椭圆
3.1.1 椭圆及其标准方程
第三章 圆锥曲线的方程
3.1 椭圆
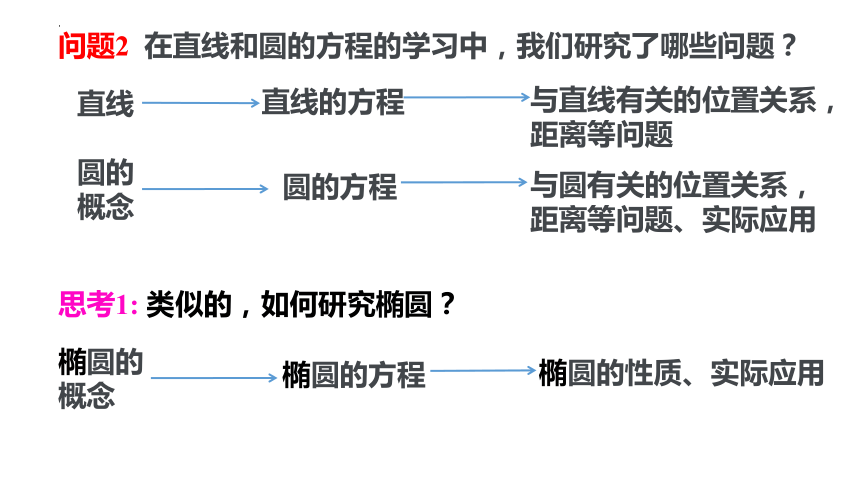
问题2 在直线和圆的方程的学习中,我们研究了哪些问题?
思考1: 类似的,如何研究椭圆?
直线
直线的方程
与直线有关的位置关系,距离等问题
圆的概念
圆的方程
与圆有关的位置关系,距离等问题、实际应用
椭圆的概念
椭圆的方程
椭圆的性质、实际应用
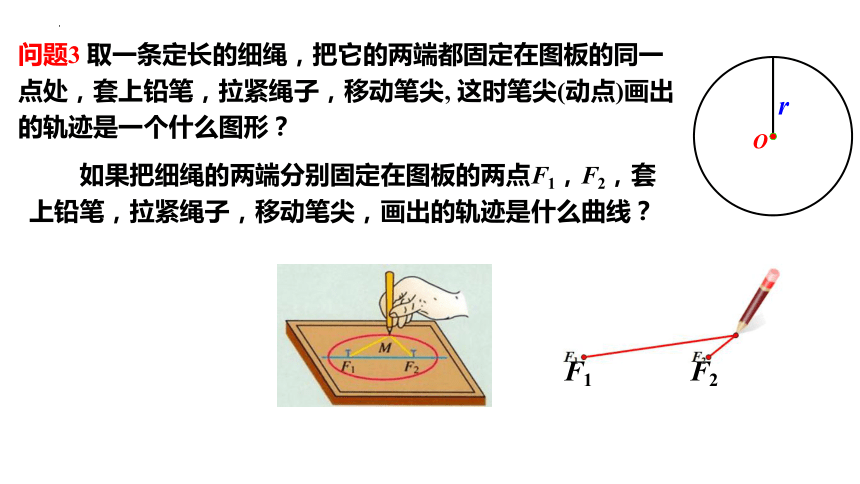
问题3 取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖, 这时笔尖(动点)画出的轨迹是一个什么图形?
·
r
O
如果把细绳的两端分别固定在图板的两点F1,F2,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
F1
F2
追问1:在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
追问2:两定点位置不动,改变绳子的长度,画出的轨迹会发生什么变化?
椭圆
线段F1F2
没有轨迹
(1)绳子长度大于两定点距离
(2)绳子长度等于两定点距离
(3)绳子长度小于两定点距离
M
F1
F2
平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1, F2叫做椭圆的焦点,两焦点之间的距离| F1F2|叫做椭圆的焦距. 焦距的一半称为半焦距.
一、椭圆的定义:
注意
① 在平面内----(这是前提条件);
② 定点F1, F2;
③ 定长:动点M到两个定点F1, F2的距离之和是常数;
动点M的轨迹是线段F1F2 ;
动点M没有轨迹 .
④
F1
F2
M
问题4 你能用精确的数学语言刻画椭圆吗?
问题5 类比求圆的标准方程的步骤,如何建立椭圆的方程?
1、建系
2、设点
3、列式
4、化简
求圆的标准方程的步骤:
追问2:椭圆是否具有某种对称性?你能猜想出椭圆的对称轴吗?
追问1:如何选取坐标系可以使所得的椭圆方程形式简单?
F1
F2
M
x
y
O
(x,y)
F1
F2
P
x
y
O
F1
F2
M
x
y
O
(x,y)
如图示, 若椭圆的焦点在x轴上, 则椭圆的标准方程为
其中焦点坐标为F1(-c,0), F2(c,0), b2=a2-c2.
二、椭圆的标准方程:
特 征:方程的左边是平方和,右边是1,“像”直线方程的截距式
标准方程:体现数学式子的简洁美、对称美,内在的每一个字母a,b都赋予它深刻的含义,最能直观体现参数几何意义。
F1
F2
M
x
y
O
F1
F2
M
x
y
O
(x,y)
(焦点在x轴上)
(焦点在y轴上)
问题7:如果椭圆的焦点F1,F2 在y轴上,且F1,F2 的坐标分别为
(0,c),(0,-c),a,b的意义同上,那么椭圆的方程是什么?
共同点:
类型一 求椭圆的标准方程:
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且过点P ,求它的标准方程.
(1) 定“位”:确定焦点的位置,
求椭圆标准方程的主要方法有:
a, b, c 满足的关系有:
(2)定“量”:求 a, b 的大小,
先定位再定量
类型一 求椭圆的标准方程:
练1 求适合下列条件的椭圆的标准方程:
例2 求适合下列条件的椭圆的标准方程:
类型一 求椭圆的标准方程:
练2 求适合下列条件的椭圆的标准方程:
课本109页
课本115页
类型一 求椭圆的标准方程:
THANKS
问题1 用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆. 如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢?
椭圆
抛物线
双曲线
圆
我们通常把椭圆、抛物线、双曲线统称为圆锥曲线
生产、生活中的圆锥曲线
行星绕太阳运行的轨道(椭圆)
发电厂冷却塔的外形线(双曲线)
卫星接收天线(抛物线)
生产、生活中的椭圆
3.1.1 椭圆及其标准方程
第三章 圆锥曲线的方程
3.1 椭圆
问题2 在直线和圆的方程的学习中,我们研究了哪些问题?
思考1: 类似的,如何研究椭圆?
直线
直线的方程
与直线有关的位置关系,距离等问题
圆的概念
圆的方程
与圆有关的位置关系,距离等问题、实际应用
椭圆的概念
椭圆的方程
椭圆的性质、实际应用
问题3 取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖, 这时笔尖(动点)画出的轨迹是一个什么图形?
·
r
O
如果把细绳的两端分别固定在图板的两点F1,F2,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
F1
F2
追问1:在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
追问2:两定点位置不动,改变绳子的长度,画出的轨迹会发生什么变化?
椭圆
线段F1F2
没有轨迹
(1)绳子长度大于两定点距离
(2)绳子长度等于两定点距离
(3)绳子长度小于两定点距离
M
F1
F2
平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1, F2叫做椭圆的焦点,两焦点之间的距离| F1F2|叫做椭圆的焦距. 焦距的一半称为半焦距.
一、椭圆的定义:
注意
① 在平面内----(这是前提条件);
② 定点F1, F2;
③ 定长:动点M到两个定点F1, F2的距离之和是常数;
动点M的轨迹是线段F1F2 ;
动点M没有轨迹 .
④
F1
F2
M
问题4 你能用精确的数学语言刻画椭圆吗?
问题5 类比求圆的标准方程的步骤,如何建立椭圆的方程?
1、建系
2、设点
3、列式
4、化简
求圆的标准方程的步骤:
追问2:椭圆是否具有某种对称性?你能猜想出椭圆的对称轴吗?
追问1:如何选取坐标系可以使所得的椭圆方程形式简单?
F1
F2
M
x
y
O
(x,y)
F1
F2
P
x
y
O
F1
F2
M
x
y
O
(x,y)
如图示, 若椭圆的焦点在x轴上, 则椭圆的标准方程为
其中焦点坐标为F1(-c,0), F2(c,0), b2=a2-c2.
二、椭圆的标准方程:
特 征:方程的左边是平方和,右边是1,“像”直线方程的截距式
标准方程:体现数学式子的简洁美、对称美,内在的每一个字母a,b都赋予它深刻的含义,最能直观体现参数几何意义。
F1
F2
M
x
y
O
F1
F2
M
x
y
O
(x,y)
(焦点在x轴上)
(焦点在y轴上)
问题7:如果椭圆的焦点F1,F2 在y轴上,且F1,F2 的坐标分别为
(0,c),(0,-c),a,b的意义同上,那么椭圆的方程是什么?
共同点:
类型一 求椭圆的标准方程:
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且过点P ,求它的标准方程.
(1) 定“位”:确定焦点的位置,
求椭圆标准方程的主要方法有:
a, b, c 满足的关系有:
(2)定“量”:求 a, b 的大小,
先定位再定量
类型一 求椭圆的标准方程:
练1 求适合下列条件的椭圆的标准方程:
例2 求适合下列条件的椭圆的标准方程:
类型一 求椭圆的标准方程:
练2 求适合下列条件的椭圆的标准方程:
课本109页
课本115页
类型一 求椭圆的标准方程:
THANKS
