第十二章 全等三角形 单元提高训练(无答案)2023-2024学年人教版八年级上册数学
文档属性
| 名称 | 第十二章 全等三角形 单元提高训练(无答案)2023-2024学年人教版八年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 177.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 00:00:00 | ||
图片预览

文档简介
第十二章 全等三角形
班级______ 姓名_______ 学号_____
一、选择题
1.下列条件中一定能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.∠A=∠D,AB=DE,BC=EF
C.AB=DE,AC=DF,BC=EF D.AB=DE,∠A=∠E,∠B=∠F
2.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( )
A.1 B.2 C.3 D.4
3.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
4.已知△ABC≌△A B C ,且△ABC的周长为20,AB=8,BC=5,则A C 等于( )
A.5 B.6 C.7 D.8
5.边长都为整数的△ABC≌△DEF,AB=2,BC=4.若△DEF周长为偶数,则DF长为( )
A.3 B.4 C.5 D.3或4或5
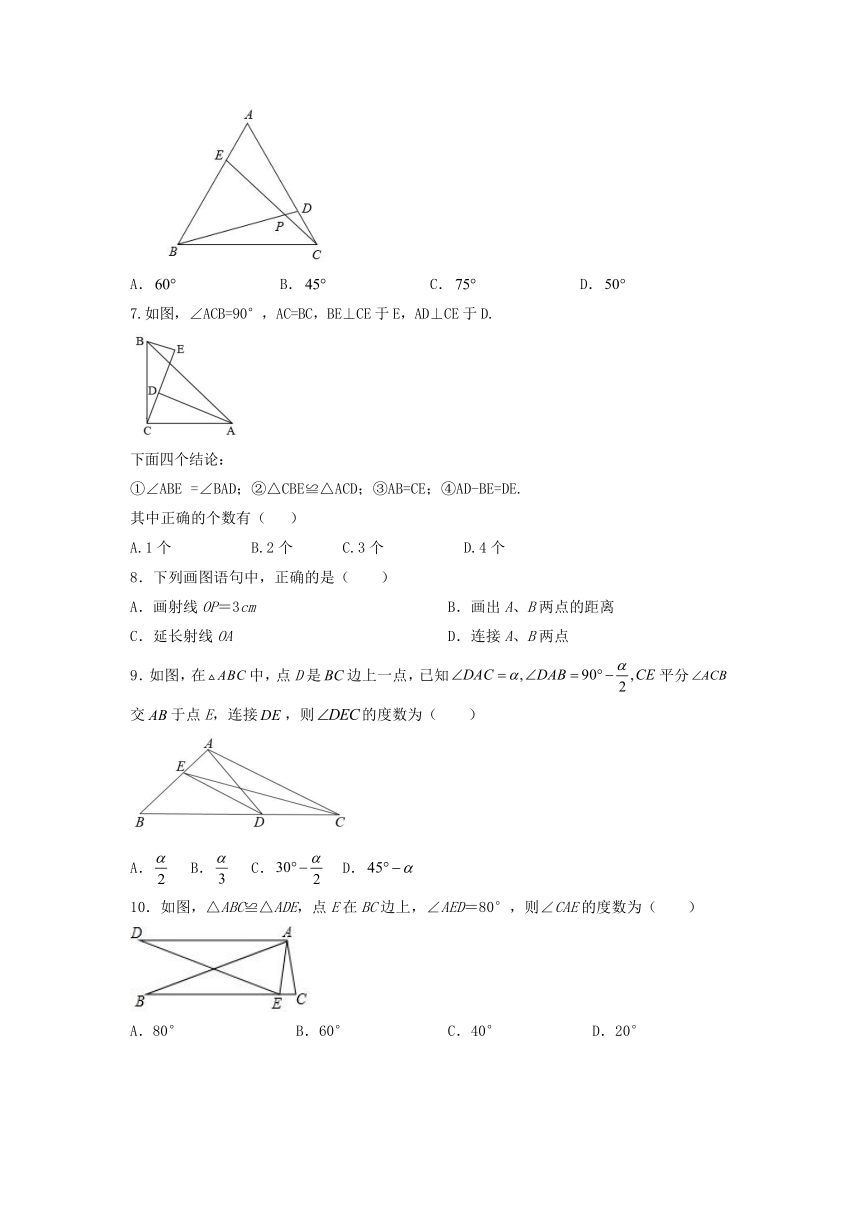
6.如图,在正中,D为上一点,E为上一点,交于P,若,则 的度数为( )
A. B. C. D.
7.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
下面四个结论:
①∠ABE =∠BAD;②△CBE≌△ACD;③AB=CE;④AD-BE=DE.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
9.如图,在中,点D是边上一点,已知平分交于点E,连接,则的度数为( )
A. B. C. D.
10.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80° B.60° C.40° D.20°
二、填空题
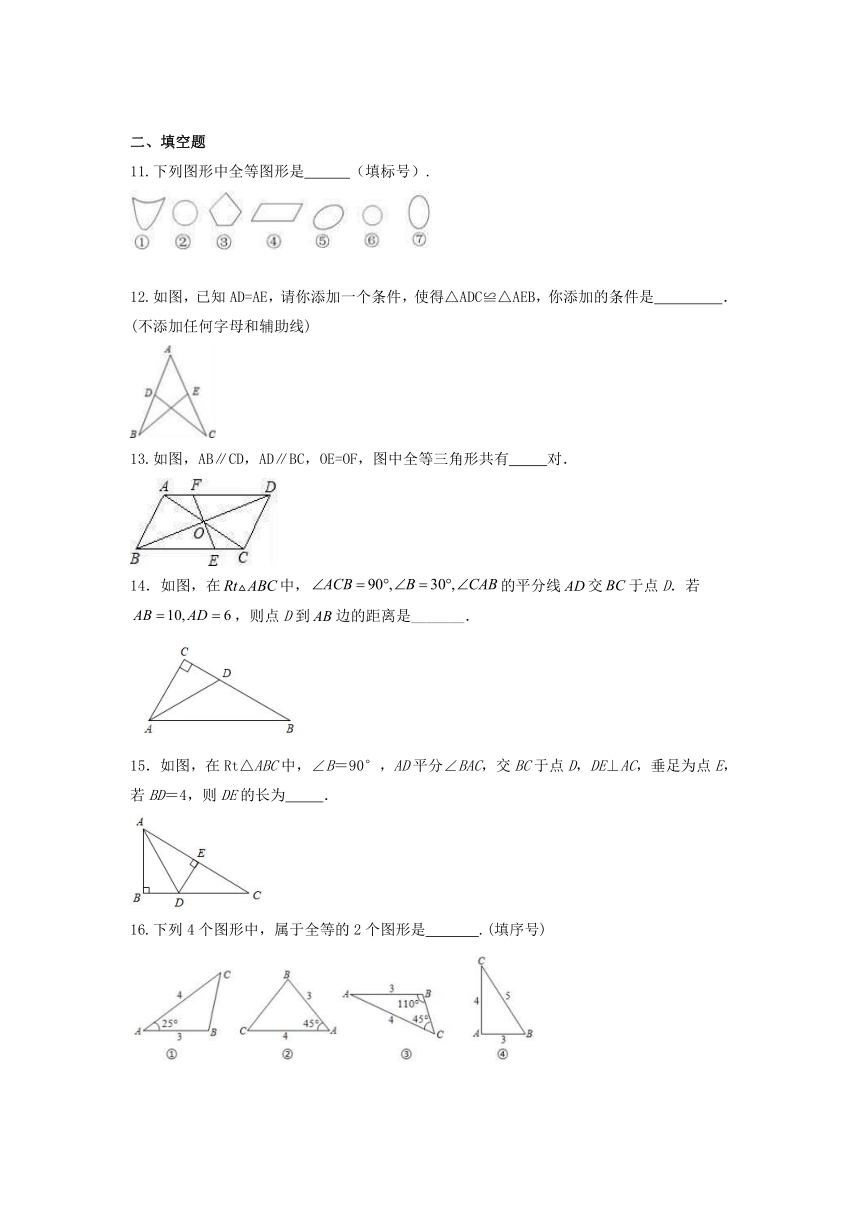
11.下列图形中全等图形是 (填标号).
12.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .
(不添加任何字母和辅助线)
13.如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有 对.
14.如图,在中,的平分线交于点D.若,则点D到边的距离是_______.
15.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为 .
16.下列4个图形中,属于全等的2个图形是 .(填序号)
17.如图,把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形,再把剩余部分(阴影部分)四周折起,恰好做成一个有底有盖的长方体纸盒,纸盒底面长方形的长为3kcm,宽为2kcm,则:
(1)裁去的每个小长方形面积为 cm2.(用k的代数式表示)
(2)若长方体纸盒的表面积是底面积的正整数倍,则正整数k的值为 .
三、解答题
18.已知:∠AOB.
求作:∠A′O′B′,使得∠A′O′B′=∠AOB.
作法:
①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;
④过点D′画射线O′B′,则∠A′O′B′=∠AOB.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).
(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).
证明:由作法可知O′C′=OC,O′D′=OD,D′C′= ,
∴△C′O′D′≌△COD( )
∴∠A′O′B′=∠AOB.( )
19.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AB∥DE.
20.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
21.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
22.(教材呈现)如图是华师版八年级上册数学教材96页的部分内容
已知:如图,是的平分线,是上任意一点,,,垂足分别为点和点.
求证: 分析:图中有两个直角三角形和,只要证明这两个三角形全等便可证得.
(问题解决)请根据教材分析,结合图①写出证明的过程.
(类比探究)
(1)如图②,是的平分线,是上任意一点,点,分别在和上,连接和,若,求证:;
(2)如图③,的周长是12,、分别平分和,于点,若,则的面积为 .
班级______ 姓名_______ 学号_____
一、选择题
1.下列条件中一定能判定△ABC≌△DEF的是( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.∠A=∠D,AB=DE,BC=EF
C.AB=DE,AC=DF,BC=EF D.AB=DE,∠A=∠E,∠B=∠F
2.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( )
A.1 B.2 C.3 D.4
3.如图,Rt△ABC中,∠C=90°,BG平分∠ABC,交AC于点G,若CG=1,P为AB上一动点,则GP的最小值为( )
A.1 B. C.2 D.无法确定
4.已知△ABC≌△A B C ,且△ABC的周长为20,AB=8,BC=5,则A C 等于( )
A.5 B.6 C.7 D.8
5.边长都为整数的△ABC≌△DEF,AB=2,BC=4.若△DEF周长为偶数,则DF长为( )
A.3 B.4 C.5 D.3或4或5
6.如图,在正中,D为上一点,E为上一点,交于P,若,则 的度数为( )
A. B. C. D.
7.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
下面四个结论:
①∠ABE =∠BAD;②△CBE≌△ACD;③AB=CE;④AD-BE=DE.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
9.如图,在中,点D是边上一点,已知平分交于点E,连接,则的度数为( )
A. B. C. D.
10.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80° B.60° C.40° D.20°
二、填空题
11.下列图形中全等图形是 (填标号).
12.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 .
(不添加任何字母和辅助线)
13.如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有 对.
14.如图,在中,的平分线交于点D.若,则点D到边的距离是_______.
15.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=4,则DE的长为 .
16.下列4个图形中,属于全等的2个图形是 .(填序号)
17.如图,把一张长方形纸板裁去两个边长为3cm的小正方形和两个全等的小长方形,再把剩余部分(阴影部分)四周折起,恰好做成一个有底有盖的长方体纸盒,纸盒底面长方形的长为3kcm,宽为2kcm,则:
(1)裁去的每个小长方形面积为 cm2.(用k的代数式表示)
(2)若长方体纸盒的表面积是底面积的正整数倍,则正整数k的值为 .
三、解答题
18.已知:∠AOB.
求作:∠A′O′B′,使得∠A′O′B′=∠AOB.
作法:
①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;
④过点D′画射线O′B′,则∠A′O′B′=∠AOB.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).
(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).
证明:由作法可知O′C′=OC,O′D′=OD,D′C′= ,
∴△C′O′D′≌△COD( )
∴∠A′O′B′=∠AOB.( )
19.如图,点B、E、C、F在同一直线上,BE=CF,AB=DE,AC=DF.
求证:AB∥DE.
20.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.
21.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
22.(教材呈现)如图是华师版八年级上册数学教材96页的部分内容
已知:如图,是的平分线,是上任意一点,,,垂足分别为点和点.
求证: 分析:图中有两个直角三角形和,只要证明这两个三角形全等便可证得.
(问题解决)请根据教材分析,结合图①写出证明的过程.
(类比探究)
(1)如图②,是的平分线,是上任意一点,点,分别在和上,连接和,若,求证:;
(2)如图③,的周长是12,、分别平分和,于点,若,则的面积为 .
