平行四边形的性质
图片预览






文档简介
课件23张PPT。 在数学的天地里,重要的不是我们知道什么,
更重要的是我们应该
怎么知道什么。 ——毕达哥拉斯 18.1.1 平行四边形的性质义务教育课程标准实验教科书数学 八年级下册观 察
学习目标:
1. 了解平行四边形的定义,表示方法.
2. 理解平行四边形的对边、对角的性质.
根据平行四边形的性质会进行简单的计算和证明;
理解两平行线间的距离。
?
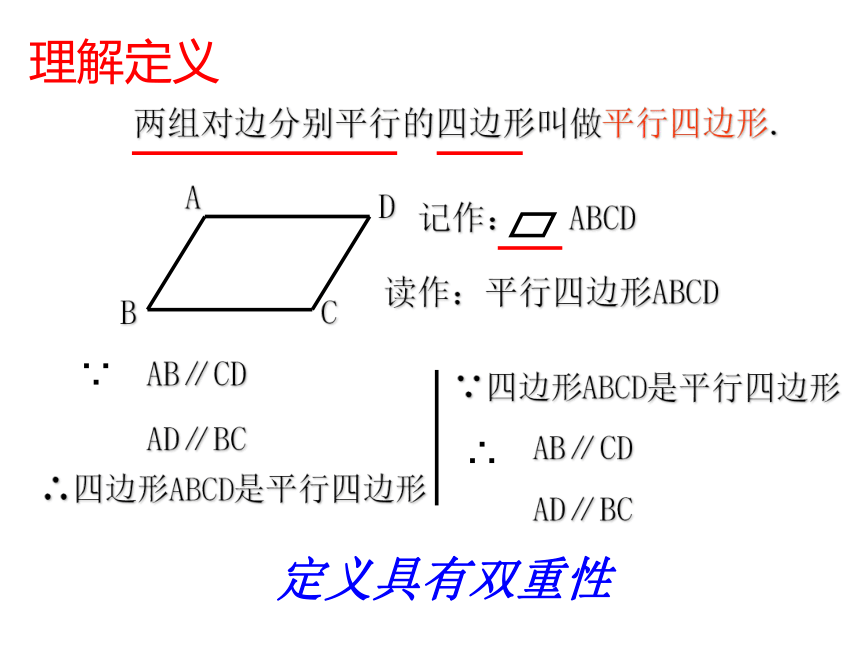
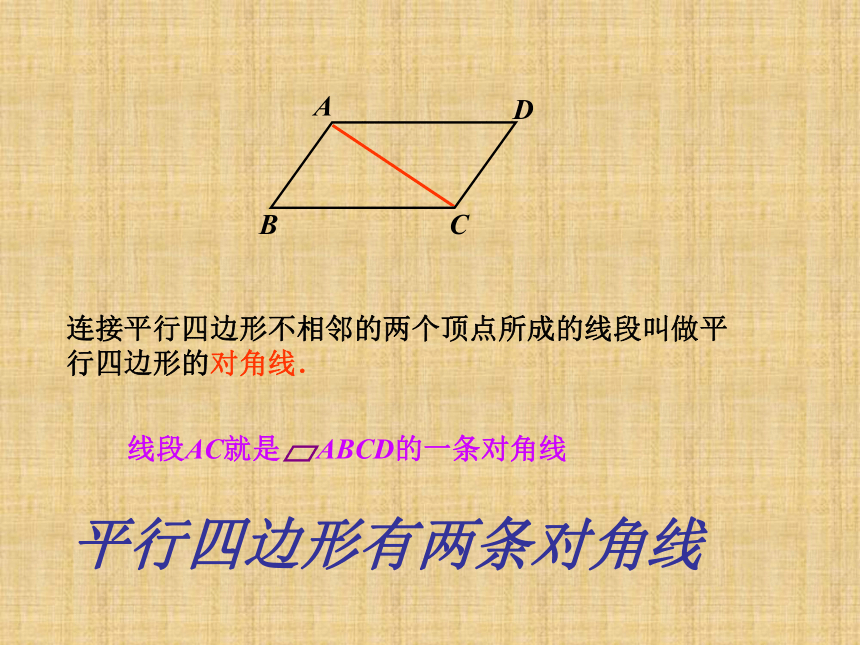
两组对边分别平行的四边形叫做平行四边形.读作:平行四边形ABCD记作: ABCD∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形理解定义定义具有双重性连接平行四边形不相邻的两个顶点所成的线段叫做平 行四边形的对角线.
平行四边形有两条对角线 (1)根据定义画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
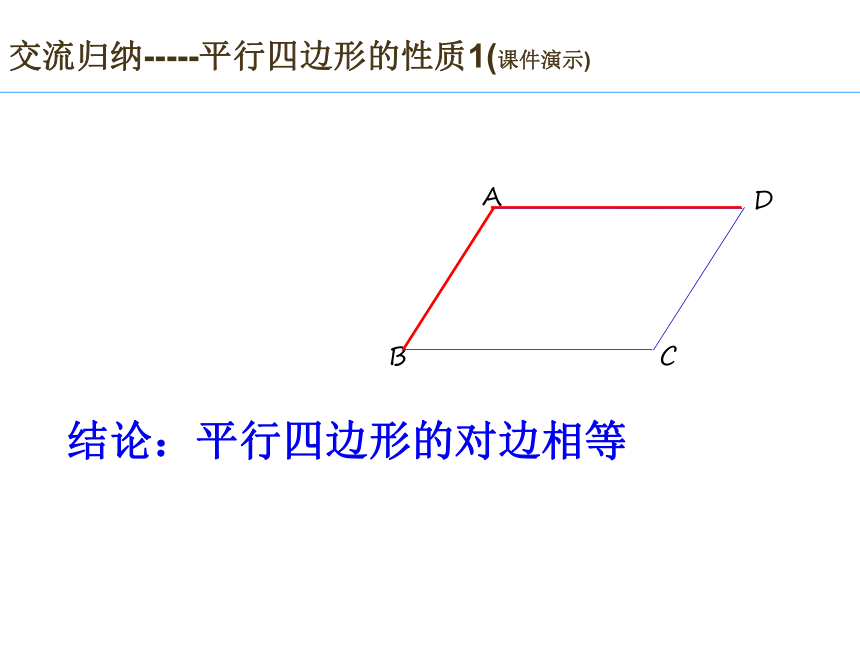
(3)度量一下,是不是和你的猜想一致?(同桌合作完成:同桌一人测量、一人记录数据,然后两人再共同分析得出边与角之间的关系)交流归纳-----平行四边形的性质1(课件演示)CBAD结论:平行四边形的对边相等交流归纳-----探索平行四边形的性质2
ABCD交流归纳-----探索平行四边形的性质
ABCD结论:平行四边形的对角相等。平行四边形的对边相等.
平行四边形的对角相等.ABCD总结归纳:如何证明解:连接BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4∵BD=DB∴△ABD≌△CDB(ASA)∴∠A=∠C AD=CB,AB=CD∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC推理证明平行四边形的性质几何语言:性质1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC.(平行四边形的对边相等)或∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 性质2:平行四边形的两组对角分别相等例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:
∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36,
∴ AD=BC=10(m).ADBC 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠C 、 ∠D的度数吗?新知应用例2 在平行四边形ABCD中, 垂足分别为求证: . Z```x``xkEFHABCDG若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.两条平行线间的距离则 GH=AD=BC.两条平行线之间的平行线段相等则 DA HG CB.(应用性质1)若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.baABCDabHG点到直线的距离==相等4030120°120°60°120°40°随堂练习? :3:如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。 课堂总结对照学习目标,谈谈本节课中有哪些收获?作业布置1、必做作业:
P49 习题18.1 第1 、2题2、选做作业:
P91 习题18.1 第7、8题感谢各位同学的配合!
感谢各位领导老师!
更重要的是我们应该
怎么知道什么。 ——毕达哥拉斯 18.1.1 平行四边形的性质义务教育课程标准实验教科书数学 八年级下册观 察
学习目标:
1. 了解平行四边形的定义,表示方法.
2. 理解平行四边形的对边、对角的性质.
根据平行四边形的性质会进行简单的计算和证明;
理解两平行线间的距离。
?
两组对边分别平行的四边形叫做平行四边形.读作:平行四边形ABCD记作: ABCD∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形理解定义定义具有双重性连接平行四边形不相邻的两个顶点所成的线段叫做平 行四边形的对角线.
平行四边形有两条对角线 (1)根据定义画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
(3)度量一下,是不是和你的猜想一致?(同桌合作完成:同桌一人测量、一人记录数据,然后两人再共同分析得出边与角之间的关系)交流归纳-----平行四边形的性质1(课件演示)CBAD结论:平行四边形的对边相等交流归纳-----探索平行四边形的性质2
ABCD交流归纳-----探索平行四边形的性质
ABCD结论:平行四边形的对角相等。平行四边形的对边相等.
平行四边形的对角相等.ABCD总结归纳:如何证明解:连接BD
∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4∵BD=DB∴△ABD≌△CDB(ASA)∴∠A=∠C AD=CB,AB=CD∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC推理证明平行四边形的性质几何语言:性质1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC.(平行四边形的对边相等)或∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 性质2:平行四边形的两组对角分别相等例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:
∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36,
∴ AD=BC=10(m).ADBC 有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠C 、 ∠D的度数吗?新知应用例2 在平行四边形ABCD中, 垂足分别为求证: . Z```x``xkEFHABCDG若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.两条平行线间的距离则 GH=AD=BC.两条平行线之间的平行线段相等则 DA HG CB.(应用性质1)若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.baABCDabHG点到直线的距离==相等4030120°120°60°120°40°随堂练习? :3:如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。 课堂总结对照学习目标,谈谈本节课中有哪些收获?作业布置1、必做作业:
P49 习题18.1 第1 、2题2、选做作业:
P91 习题18.1 第7、8题感谢各位同学的配合!
感谢各位领导老师!
