苏科版八年级数学上册试题 第3章 勾股定理 单元检测卷(含答案)
文档属性
| 名称 | 苏科版八年级数学上册试题 第3章 勾股定理 单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 703.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 19:21:06 | ||
图片预览




文档简介
第3章《勾股定理》单元检测卷
一、选择题(本大题共12小题,每小题3分,共36分).
1.根据勾股定理,任意直角三角形的两条直角边长 , ,和斜边长都是含三个未知数的方程 的一组解,而每一组勾股数(例如3,4,5;5,12,13;等)都是这个方程的正整数解.高于二次的方程,,,…是否也有正整数解呢?法国数学家费马经过研究得出结论:当自然数 时,方程没有正整数解.这个命题的证明引起了世界各国数学家的关注,最终由英国数学家怀尔斯于1995年完成了证明.困扰了数学家300多年历史的数学难题终于得到解决,在解决这一数学难题的过程中,反映了一代代数学家艰苦探索、不屈不挠的科学精神和聪明慧.这个定理的证明被称为“世纪性的成就”.这个定理指的是( )
A.费马大定理 B.怀尔斯大定理 C.勾股定理 D.勾股定理的逆定理
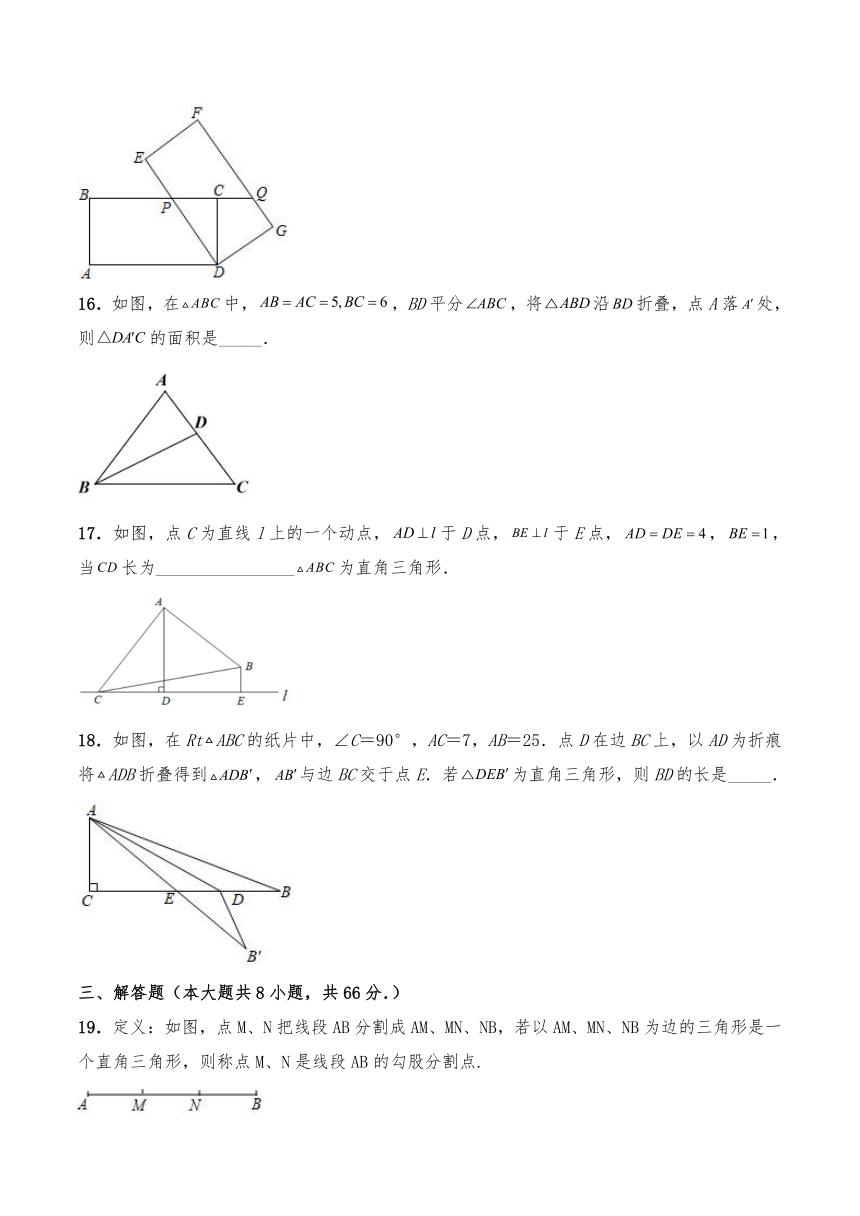
2.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形,且∠C=90°
C.如果∠A︰∠B︰∠C=1︰3︰2,那么△ABC是直角三角形
D.如果a2︰b2︰c2=9︰16︰25,那么△ABC是直角三角形
3.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
4.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
5.如图,在△ABC中,CE平分∠ACB,CF平分△ABC的外角∠ACD,且EF∥BC交AC于M,若CM=4,则CE2+CF2的值为( )
A.8 B.16 C.32 D.64
6.如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
7.如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )
A.5 B.7 C.12 D.
8.已知直角三角形的面积为6cm2,两直角边的和为7cm,则它的斜边长为( )cm.
A.5 B.6 C. D.
9.如图,已知图中所有的四边形都是正方形,所有的三角形都是直角三角形.若其中每个直角三角形的最长边与最短边的长度之比均为,正方形,,,的面积分别为,,,,且,则下列结论正确的是( )
A. B. C. D.
10.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若,则S2的值是( )
A.9 B.8 C.7 D.6
11.如图,中,,,,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为( )
A. B. C. D.
12.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④ B.①②④ C.①③④ D.②③
二、填空题(本大题共6小题,每小题3分,共18分.)
13.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为__尺.
14.如图,在正方形网格中,每个小正方形的边长为是网格上的格点三角形,则它的边上的高等于_______.
15.如图,矩形中,,,将矩形绕点顺时针旋转得到矩形,边与交于点,延长交于点,若,则的长为______.
16.如图,在中,,BD平分,将沿折叠,点A落处,则的面积是_____.
17.如图,点C为直线l上的一个动点,于D点,于E点,,,当长为________________为直角三角形.
18.如图,在RtABC的纸片中,∠C=90°,AC=7,AB=25.点D在边BC上,以AD为折痕将ADB折叠得到,与边BC交于点E.若为直角三角形,则BD的长是_____.
三、解答题(本大题共8小题,共66分.)
19.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段分割成AM、MN、NB,若,,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.
20.年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
21.今年的气候变化很大,极端天气频繁出现.某沿海城市气象台监测到台风中心
位于正东方向的海上.如图所示,城市所在地为A,台风中心O正以每小时的速度向北偏西60°的方向移动,经监测得知台风中心的范围内将会受台风影响,.该城市是否受到这次台风的影响?若不受影响,请说明理由;若受到这次台风影响,请求出遭受这次台风影响的时间.
22.勾股定理是一个基本的几何定理,尽在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”,这三个整数叫做一组“勾股数”.如:等等都是勾股数.
(探究1)
(1)如果是一组勾股数,即满足,则为正整数)也是一组勾股数.如;是一组勾股数,则__ _也是一组勾股数;
(2)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派就曾提出公式为正整数)是一组勾股数,证明满足以上公式的是一组勾股数;
(3)值得自豪的是,世界上第一次给出的勾股数公式,收集在我国的《九章算术》中, 书中提到:当,为正整数,时,构成一组勾股数;请根据这一结论直接写出一组符合条件的勾股数___ .
(探究2)
观察;…,可以发现这些勾股数的勾都是奇数,且从起就没有间断过,并且勾为时股,弦;勾为时,股,弦;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股___ _;弦___ _;
(2)如果用且为奇数)表示勾,请用含有的式子表示股和弦,则股___ ;弦__ _;
(3)观察;…,可以发现各组的第一个数都是偶数,且从起也没有间断过.
_;请你直接用为偶数且)的代数式表示直角三角形的另一条直角边_ ;和弦的长_ _.
23.在中,,,.如图1,若时,根据勾股定理有.(1)如图2,当为锐角三角形时,类比勾股定理,判断与的大小关系,并证明;(2)如图3,当为钝角三角形时,类比勾股定理,判断与的大小关系,并证明;
(3)如图4,一块四边形的试验田,已知,米,米,米,米,求这块试验田的面积.
24.勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.
(探究一)我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).
请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).
(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积,,之间满足的等量关系是:__________.
迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形,,,的边长分别是,,,,则正方形的面积是________.
(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________.
迁移应用:如图5,直角三角形的两条直角边长分别为,,斜边长为,分别以三边为直径作半圆.若,,则图中阴影部分的面积等于________.
(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有尺.牵着绳索(绳索与地面接触)退行,在距木柱根部尺处时绳索用尽.问绳索长多少?
25.如图,在公路的同侧有两个居民点、,居民点、分别到公路的距离千米和千米,且两个居民点、相距千米.
(1)要在公路边修一个污水处理站来收集处理居民点、的污水,污水处理站修在什么地方到居民点、所用的水管最短;请你在图中设计出污水处理站的位置.(保留作图痕迹,不要证明)
(2)如图铺设水管的工程费用为每千米万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)要在公路边修一个汽车站,使汽车站到两个居民点、的距离相等,则点应该修在距点多远的地方(另画图并写出解答过程)
26.已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 ,并猜想BC和CE、CD之间的数量关系: .
尝试探究:(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系,BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:(3)如图3,当点D在边CB的延长线上且其他条件不变时,若BC=7,CE=5,直接写出线段ED的长.
答案
一、选择题
A.B.B.A.D.B.B.A.D.C.A.A.
二、填空题
13.12.
14.
15.(
16.
17.3或2或.
18.17或
三、解答题
19.解:(1)是.理由:,, ,,,
,、、为边的三角形是一个直角三角形.
即:点M、N是线段AB的勾股分割点.
(2)设,则,
①当为最长线段时,依题意,即,解得,
②当为最长线段时,依题意.即,解得,
综上所述的长为或.
20.(1)测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.(或:勾股定理的逆定理).
(2)如图,连接,
,,,,由勾股定理,得,
又,,,是直角三角形,
..
绿化费用为:(元).答:绿化这片空地共需要元.
21.解:如图,过点A作于点C,
由题得,,∴,
∵,∴会受到台风影响. 以A为圆心,以200米长为半径画弧交OB与D、G两点,
∴AD=AG=200千米,在Rt△ADC中,DA=200千米,AC=160千米,
由勾股定理得,(千米),同理可得CG=120,则DG=240千米,
∴A城遭受台风影响的时间是:t=240÷40=6(小时).
22.探究1:(1)6,8,10(答案不唯一);·
(2)证明:
,
,满足以上公式的是一组勾股数;
(3)∵=∴满足以上公式的是一组勾股数;
当时,,
∴构成一组勾股数.(答案不唯一)
探究2:(1)依据规律可得,如果勾为,则股,弦,
(2)如果勾用,且为奇数)表示时,
则股, 弦
(3)①b=80.②根据规律可得,如果是符合同样规律的一组勾股数,为偶数且),
则另一条直角边 弦
23.解:(1)猜想: ,
证明:如图2,过点作于点,设,则,
在Rt中,有, 在Rt中,有 ,
∴ ,解之:,
∵均为正数,∴ ;
(2)猜想: 证明:如图3,过点作,交的延长线于点,设,则,
在Rt中,有,在Rt中,有 ,
∴,解之:,∵均为正数,∴ ;
(3)如图4,连接.在Rt中,有,∴,
∵,∴ ,过点作于点E,设,则EC=100-x,
在Rt中,有,即,
在Rt中,有,即 ,∴,解之:,
在Rt中,有,∴DE=(取正),∴DE=,
∴,=(米2),
∴四边形ABCD的面积是米2.
24.解:【探究一】:由题意得:②的面积为a2+b2+2ab=a2+b2+ab;
图③的面积为c2+2ab=c2+ab,
∴a2+b2+ab=c2+ab,即a2+b2=c2;
【探究二】S1+S2=S3.
证明如下:∵S3=c2,S1=a2,S2=b2,
∴S1+S2=a2+b2=c2=S3;故答案为:S1+S2=S3;
迁移应用:根据勾股定理的几何意义,可知
SE=SF+SG=SA+SB+SC+SD=32+52+32+22=47;故答案为:47;
【探究三】S1+S2=S3.
证明如下:∵S3=πc2,S1=πa2,S2=πb2,
∴S1+S2= πa2+πb2=πc2=S3;故答案为:S1+S2=S3;
迁移应用:阴影部分面积和=S1+S2+ab-S3=ab,
∵a=5,c=13,∴12,
∴阴影部分面积和=×5×12=30,故答案为:30;
【探究四】设绳索长为x尺,根据题意得:x2-(x-3)2=82,解得:x=,
答:绳索长为尺.
25.(1)如图1所示,点即为所求.
(2)如图1,过点作于点,过点作,交延长线于点,
则四边形和四边形均为矩形,
,,则,,
在中,,,
则,所以最节省的费用为(万元).
(3)如图,作的中垂线,交于点,则点即为所求;
连接、,设,则,
,,即,
解得:,即点在距离点的地方.
26.解:(1)如图1,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,∴∠BCE=45°+45°=90°,即BD⊥CE.
∴BC=BD+CD=CE+CD,
故答案为:BD⊥CE(或“垂直”),BC=CE+CD (或CE = BC –CD或CD = BC- CE);
(2)BD⊥CE成立,数量关系不成立,关系为BC=CE﹣CD.
理由:如图2中,由(1)同理可得,
∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD即∠BAD=∠CAE,
∴在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC,
∵AB=AC,∴∠ABC=∠ACB=45°,
∴BD=BC+CD,即CE=BC+CD,∠ACE+∠ACB=90°,∴BC=CE﹣CD;BD⊥CE;
(3)如图3中,由(1)同理可得,
∵∠BAC=∠DAE=90°,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠BAD=∠EAC,同理,△ABD≌△ACE(SAS),
∴BD=CE=5,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE=12,
∵∠ACB=45°∴∠DCE=90°,
在Rt△DCE中,由勾股定理得DE2=DC2+CE2=122+52=132,∴DE=13.
一、选择题(本大题共12小题,每小题3分,共36分).
1.根据勾股定理,任意直角三角形的两条直角边长 , ,和斜边长都是含三个未知数的方程 的一组解,而每一组勾股数(例如3,4,5;5,12,13;等)都是这个方程的正整数解.高于二次的方程,,,…是否也有正整数解呢?法国数学家费马经过研究得出结论:当自然数 时,方程没有正整数解.这个命题的证明引起了世界各国数学家的关注,最终由英国数学家怀尔斯于1995年完成了证明.困扰了数学家300多年历史的数学难题终于得到解决,在解决这一数学难题的过程中,反映了一代代数学家艰苦探索、不屈不挠的科学精神和聪明慧.这个定理的证明被称为“世纪性的成就”.这个定理指的是( )
A.费马大定理 B.怀尔斯大定理 C.勾股定理 D.勾股定理的逆定理
2.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形,且∠C=90°
C.如果∠A︰∠B︰∠C=1︰3︰2,那么△ABC是直角三角形
D.如果a2︰b2︰c2=9︰16︰25,那么△ABC是直角三角形
3.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
4.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
5.如图,在△ABC中,CE平分∠ACB,CF平分△ABC的外角∠ACD,且EF∥BC交AC于M,若CM=4,则CE2+CF2的值为( )
A.8 B.16 C.32 D.64
6.如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
7.如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为( )
A.5 B.7 C.12 D.
8.已知直角三角形的面积为6cm2,两直角边的和为7cm,则它的斜边长为( )cm.
A.5 B.6 C. D.
9.如图,已知图中所有的四边形都是正方形,所有的三角形都是直角三角形.若其中每个直角三角形的最长边与最短边的长度之比均为,正方形,,,的面积分别为,,,,且,则下列结论正确的是( )
A. B. C. D.
10.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若,则S2的值是( )
A.9 B.8 C.7 D.6
11.如图,中,,,,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点处,两条折痕与斜边AB分别交于点E、F,则线段的长为( )
A. B. C. D.
12.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④ B.①②④ C.①③④ D.②③
二、填空题(本大题共6小题,每小题3分,共18分.)
13.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为__尺.
14.如图,在正方形网格中,每个小正方形的边长为是网格上的格点三角形,则它的边上的高等于_______.
15.如图,矩形中,,,将矩形绕点顺时针旋转得到矩形,边与交于点,延长交于点,若,则的长为______.
16.如图,在中,,BD平分,将沿折叠,点A落处,则的面积是_____.
17.如图,点C为直线l上的一个动点,于D点,于E点,,,当长为________________为直角三角形.
18.如图,在RtABC的纸片中,∠C=90°,AC=7,AB=25.点D在边BC上,以AD为折痕将ADB折叠得到,与边BC交于点E.若为直角三角形,则BD的长是_____.
三、解答题(本大题共8小题,共66分.)
19.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段分割成AM、MN、NB,若,,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.
20.年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
21.今年的气候变化很大,极端天气频繁出现.某沿海城市气象台监测到台风中心
位于正东方向的海上.如图所示,城市所在地为A,台风中心O正以每小时的速度向北偏西60°的方向移动,经监测得知台风中心的范围内将会受台风影响,.该城市是否受到这次台风的影响?若不受影响,请说明理由;若受到这次台风影响,请求出遭受这次台风影响的时间.
22.勾股定理是一个基本的几何定理,尽在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”,这三个整数叫做一组“勾股数”.如:等等都是勾股数.
(探究1)
(1)如果是一组勾股数,即满足,则为正整数)也是一组勾股数.如;是一组勾股数,则__ _也是一组勾股数;
(2)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派就曾提出公式为正整数)是一组勾股数,证明满足以上公式的是一组勾股数;
(3)值得自豪的是,世界上第一次给出的勾股数公式,收集在我国的《九章算术》中, 书中提到:当,为正整数,时,构成一组勾股数;请根据这一结论直接写出一组符合条件的勾股数___ .
(探究2)
观察;…,可以发现这些勾股数的勾都是奇数,且从起就没有间断过,并且勾为时股,弦;勾为时,股,弦;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股___ _;弦___ _;
(2)如果用且为奇数)表示勾,请用含有的式子表示股和弦,则股___ ;弦__ _;
(3)观察;…,可以发现各组的第一个数都是偶数,且从起也没有间断过.
_;请你直接用为偶数且)的代数式表示直角三角形的另一条直角边_ ;和弦的长_ _.
23.在中,,,.如图1,若时,根据勾股定理有.(1)如图2,当为锐角三角形时,类比勾股定理,判断与的大小关系,并证明;(2)如图3,当为钝角三角形时,类比勾股定理,判断与的大小关系,并证明;
(3)如图4,一块四边形的试验田,已知,米,米,米,米,求这块试验田的面积.
24.勾股定理是人类重大科学发现之一.我国古代数学书《周髀算经》记载,约公元前11世纪,我国古代劳动人民就知道“若勾三,股四,则弦五”,比西方早500多年.请你运用学到的知识、方法和思想探究以下问题.
(探究一)我国汉代数学家赵爽创制了“赵爽弦图”,通过图形切割、拼接,巧妙地利用面积关系证明了勾股定理.古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用两张一样的纸片,拼出不一样的空洞,利用空洞面积相等也成功地证明了勾股定理(如图).
请你写出这一证明过程(图中所有的四边形都是正方形,三角形都是直角三角形).
(探究二)在学习勾股定理的过程中,我们获得了以下数学活动经验:分别以直角三角形的三边为边向外侧作正方形(如图2),它们的面积,,之间满足的等量关系是:__________.
迁移应用:如图3,图中所有的四边形都是正方形,三角形都是直角三角形.若正方形,,,的边长分别是,,,,则正方形的面积是________.
(探究三)如图4,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________.
迁移应用:如图5,直角三角形的两条直角边长分别为,,斜边长为,分别以三边为直径作半圆.若,,则图中阴影部分的面积等于________.
(探究四)《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尺.问索长几何.译文:今有一竖立着的木柱,在木桩的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有尺.牵着绳索(绳索与地面接触)退行,在距木柱根部尺处时绳索用尽.问绳索长多少?
25.如图,在公路的同侧有两个居民点、,居民点、分别到公路的距离千米和千米,且两个居民点、相距千米.
(1)要在公路边修一个污水处理站来收集处理居民点、的污水,污水处理站修在什么地方到居民点、所用的水管最短;请你在图中设计出污水处理站的位置.(保留作图痕迹,不要证明)
(2)如图铺设水管的工程费用为每千米万元,为使铺设水管的费用最节省,请求出最节省的费用为多少万元?(3)要在公路边修一个汽车站,使汽车站到两个居民点、的距离相等,则点应该修在距点多远的地方(另画图并写出解答过程)
26.已知△ABC中,∠BAC=90°,AB=AC,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作△ADE,使∠DAE=90°,AD=AE,连接CE.
发现问题:如图1,当点D在边BC上时,
(1)请写出BD和CE之间的位置关系为 ,并猜想BC和CE、CD之间的数量关系: .
尝试探究:(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中BD和CE之间的位置关系,BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;
拓展延伸:(3)如图3,当点D在边CB的延长线上且其他条件不变时,若BC=7,CE=5,直接写出线段ED的长.
答案
一、选择题
A.B.B.A.D.B.B.A.D.C.A.A.
二、填空题
13.12.
14.
15.(
16.
17.3或2或.
18.17或
三、解答题
19.解:(1)是.理由:,, ,,,
,、、为边的三角形是一个直角三角形.
即:点M、N是线段AB的勾股分割点.
(2)设,则,
①当为最长线段时,依题意,即,解得,
②当为最长线段时,依题意.即,解得,
综上所述的长为或.
20.(1)测量的是点,之间的距离;
依据是:如果三角形的三边长,,满足,那么这个三角形是直角三角形.(或:勾股定理的逆定理).
(2)如图,连接,
,,,,由勾股定理,得,
又,,,是直角三角形,
..
绿化费用为:(元).答:绿化这片空地共需要元.
21.解:如图,过点A作于点C,
由题得,,∴,
∵,∴会受到台风影响. 以A为圆心,以200米长为半径画弧交OB与D、G两点,
∴AD=AG=200千米,在Rt△ADC中,DA=200千米,AC=160千米,
由勾股定理得,(千米),同理可得CG=120,则DG=240千米,
∴A城遭受台风影响的时间是:t=240÷40=6(小时).
22.探究1:(1)6,8,10(答案不唯一);·
(2)证明:
,
,满足以上公式的是一组勾股数;
(3)∵=∴满足以上公式的是一组勾股数;
当时,,
∴构成一组勾股数.(答案不唯一)
探究2:(1)依据规律可得,如果勾为,则股,弦,
(2)如果勾用,且为奇数)表示时,
则股, 弦
(3)①b=80.②根据规律可得,如果是符合同样规律的一组勾股数,为偶数且),
则另一条直角边 弦
23.解:(1)猜想: ,
证明:如图2,过点作于点,设,则,
在Rt中,有, 在Rt中,有 ,
∴ ,解之:,
∵均为正数,∴ ;
(2)猜想: 证明:如图3,过点作,交的延长线于点,设,则,
在Rt中,有,在Rt中,有 ,
∴,解之:,∵均为正数,∴ ;
(3)如图4,连接.在Rt中,有,∴,
∵,∴ ,过点作于点E,设,则EC=100-x,
在Rt中,有,即,
在Rt中,有,即 ,∴,解之:,
在Rt中,有,∴DE=(取正),∴DE=,
∴,=(米2),
∴四边形ABCD的面积是米2.
24.解:【探究一】:由题意得:②的面积为a2+b2+2ab=a2+b2+ab;
图③的面积为c2+2ab=c2+ab,
∴a2+b2+ab=c2+ab,即a2+b2=c2;
【探究二】S1+S2=S3.
证明如下:∵S3=c2,S1=a2,S2=b2,
∴S1+S2=a2+b2=c2=S3;故答案为:S1+S2=S3;
迁移应用:根据勾股定理的几何意义,可知
SE=SF+SG=SA+SB+SC+SD=32+52+32+22=47;故答案为:47;
【探究三】S1+S2=S3.
证明如下:∵S3=πc2,S1=πa2,S2=πb2,
∴S1+S2= πa2+πb2=πc2=S3;故答案为:S1+S2=S3;
迁移应用:阴影部分面积和=S1+S2+ab-S3=ab,
∵a=5,c=13,∴12,
∴阴影部分面积和=×5×12=30,故答案为:30;
【探究四】设绳索长为x尺,根据题意得:x2-(x-3)2=82,解得:x=,
答:绳索长为尺.
25.(1)如图1所示,点即为所求.
(2)如图1,过点作于点,过点作,交延长线于点,
则四边形和四边形均为矩形,
,,则,,
在中,,,
则,所以最节省的费用为(万元).
(3)如图,作的中垂线,交于点,则点即为所求;
连接、,设,则,
,,即,
解得:,即点在距离点的地方.
26.解:(1)如图1,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,∴∠BCE=45°+45°=90°,即BD⊥CE.
∴BC=BD+CD=CE+CD,
故答案为:BD⊥CE(或“垂直”),BC=CE+CD (或CE = BC –CD或CD = BC- CE);
(2)BD⊥CE成立,数量关系不成立,关系为BC=CE﹣CD.
理由:如图2中,由(1)同理可得,
∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD即∠BAD=∠CAE,
∴在△ABD和△ACE中,,
∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC,
∵AB=AC,∴∠ABC=∠ACB=45°,
∴BD=BC+CD,即CE=BC+CD,∠ACE+∠ACB=90°,∴BC=CE﹣CD;BD⊥CE;
(3)如图3中,由(1)同理可得,
∵∠BAC=∠DAE=90°,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠BAD=∠EAC,同理,△ABD≌△ACE(SAS),
∴BD=CE=5,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE=12,
∵∠ACB=45°∴∠DCE=90°,
在Rt△DCE中,由勾股定理得DE2=DC2+CE2=122+52=132,∴DE=13.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
