第18章 平行四边形综合检测试题

单元综合检测(三)
第18章
(45分钟　100分)
一、选择题(每小题4分，共28分)
1.在□ABCD中，AD=3cm，AB=2cm，则□ABCD的周长等于(　　)
A.10 cm　　 B.6 cm　 　C.5 cm　 　D.4 cm
2.如图，四边形ABCD是平行四边形，点E在边BC上.如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是(　　)
( http: / / www.21cnjy.com )
A.DF=BE B.AF=CE
C.CF=AE D.CF∥AE
3.平行四边形两邻角的平分线相交所成的角为(　　)
A.锐角 B.直角 C.钝角 D.不确定
4.如图，在平行四边形ABCD中，下列各式不一定正确的是(　　)
( http: / / www.21cnjy.com )
A.∠1+∠2=180° B.∠2+∠3=180°
C.∠3+∠4=180° D.∠2+∠4=180°
5.(2013·哈尔滨中考)如图，在□ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，则AB的长为(　　)
( http: / / www.21cnjy.com )
A.4　 B.3 　 C.　 D.2
6.如图，在平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA的取值范围是(　　)
( http: / / www.21cnjy.com )
A.3cmC.1cm7.(2013·达州中考)如图，在Rt△ ( http: / / www.21cnjy.com )ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有□ADCE中，DE最小的值是(　　)
( http: / / www.21cnjy.com )
A.2　　　　B.3　　　　C.4　　　　D.5
二、填空题(每小题5分，共25分)
8.如图，在□ABCD中，∠A=120°，则∠D=　　　　°.
( http: / / www.21cnjy.com )
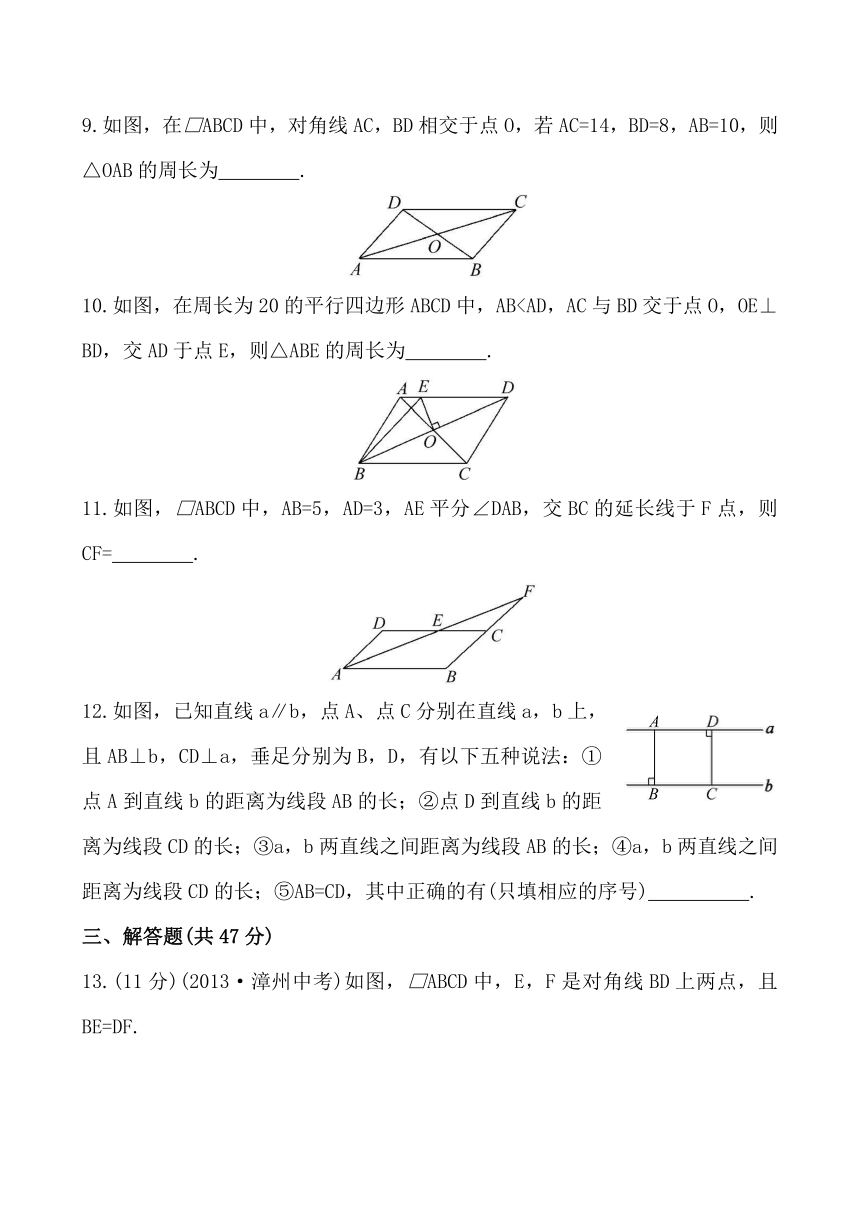
9.如图，在□ABCD中，对角线AC，BD相交于点O，若AC=14，BD=8，AB=10，则△OAB的周长为　　　　.
( http: / / www.21cnjy.com )
10.如图，在周长为20的平行四边形ABCD中，AB( http: / / www.21cnjy.com )
11.如图，□ABCD中，AB=5，AD=3，AE平分∠DAB，交BC的延长线于F点，则CF=　　　　.
( http: / / www.21cnjy.com )
12.如图，已知直线a∥b，点A、点C分别 ( http: / / www.21cnjy.com )在直线a，b上，且AB⊥b，CD⊥a，垂足分别为B，D，有以下五种说法：①点A到直线b的距离为线段AB的长；②点D到直线b的距离为线段CD的长；③a，b两直线之间距离为线段AB的长；④a，b两直线之间距离为线段CD的长；⑤AB=CD，其中正确的有(只填相应的序号)　　　　　.
三、解答题(共47分)
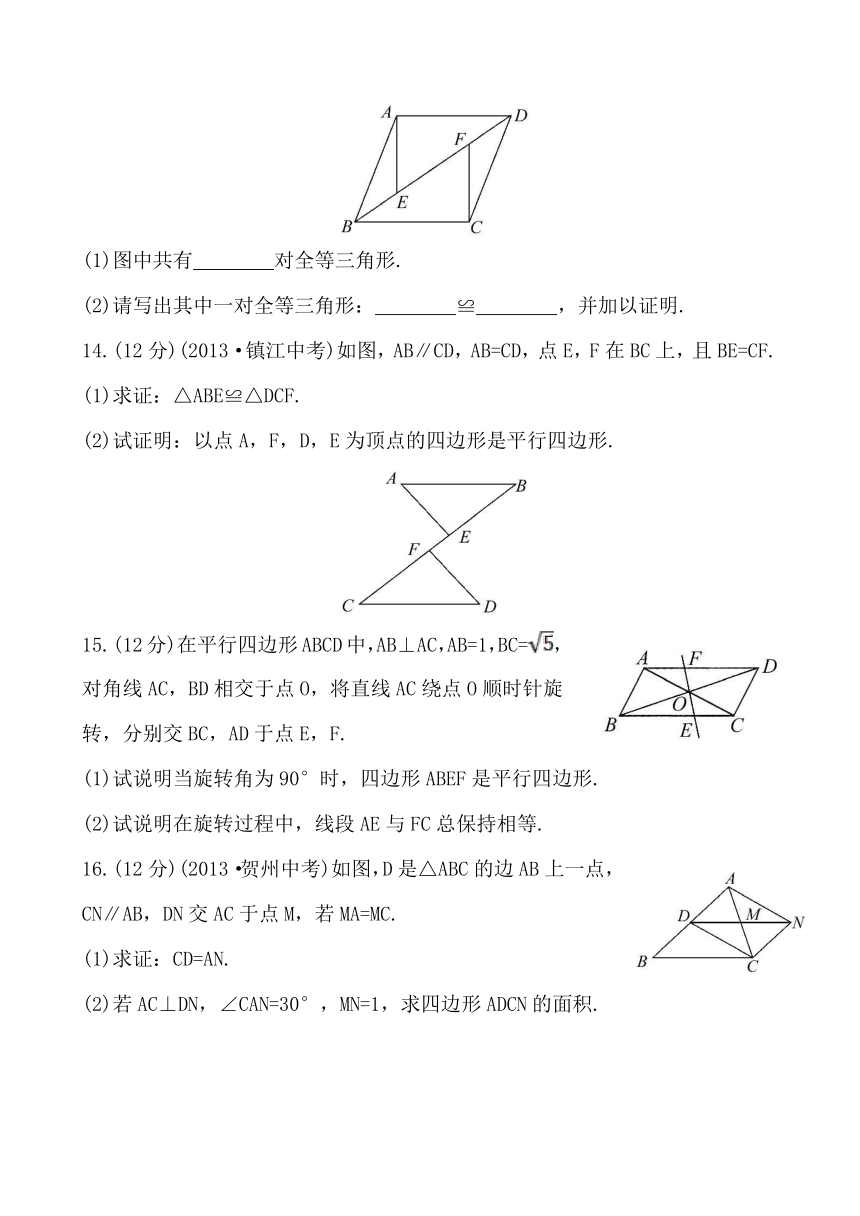
13.(11分)(2013·漳州中考)如图，□ABCD中，E，F是对角线BD上两点，且BE=DF.
( http: / / www.21cnjy.com )
(1)图中共有　　　　对全等三角形.
(2)请写出其中一对全等三角形：　　　　≌　　　　，并加以证明.
14.(12分)(2013·镇江中考)如图，AB∥CD，AB=CD，点E，F在BC上，且BE=CF.
(1)求证：△ABE≌△DCF.
(2)试证明：以点A，F，D，E为顶点的四边形是平行四边形.
( http: / / www.21cnjy.com )
15.(12分)在平行四边形ABCD中，AB⊥AC，AB=1，BC=，对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F.
(1)试说明当旋转角为90°时，四边形ABEF是平行四边形.
(2)试说明在旋转过程中，线段AE与FC总保持相等.
16.(12分)(2013·贺州中考)如图，D是△ABC的边AB上一点，CN∥AB，DN交AC于点M，若MA=MC.
(1)求证：CD=AN.
(2)若AC⊥DN，∠CAN=30°，MN=1，求四边形ADCN的面积.
答案解析
1.【解析】选A.因为平行四边形的对边相等，所以AD=BC=3cm，AB=CD=2cm，所以周长为10 cm.
2.【解析】选C.由平行四边形的性质可得A ( http: / / www.21cnjy.com )B=CD，AD=BC，∠B=∠D等.A中，DF=BE，∠B=∠D，AB=CD，符合“边角边”定理，△CDF≌△ABE，选项A成立；B中，AF=CE，可得DF=BE，同选项A，选项B成立；C中，CF=AE，∠B=∠D，AB=CD，条件为两边及一边的对角，C不一定成立；D中，CF∥AE，可得四边形AECF是平行四边形，得AF=CE，所以BE=DF，同选项A，该选项成立.综上所述，选C.
3.【解析】选B.□ABCD的∠DAB的平分线和∠ABC的平分线交于O，∴∠DAB+∠ABC=180°，∠DAO=∠BAO=∠DAB，∠ABO=∠CBO=∠ABC，∴∠BAO+∠ABO=90°，
∴∠AOB=180°-90°=90°.
4.【解析】选D.由平行四 ( http: / / www.21cnjy.com )边形的性质及图形可知：∠1和∠2是邻补角，故∠1+∠2=180°，A正确；因为AD∥BC，所以∠2+∠3=180°，B正确；因为AB∥CD，所以∠3+∠4=180°，C正确；D.根据平行四边形的对角相等，∠2=∠4，∠2+∠4=180°不一定正确，故选D.
5.【解析】选B.在□ABCD中，AD∥BC，∴∠DEC=∠BCE，∵CE平分∠BCD，
∴∠BCE=∠DCE，∴∠DEC=∠DCE，∴DC=DE.
又∵AD=2AB，AB=CD，AE=3，∴AB=3.
6.【解析】选C.在△ABC中，BC-AB7.【解析】选B.∵四边形ADCE是平行四边形，
∴OD=OE，OA=OC.∴当OD取最小值时，
DE线段最短，此时BC⊥DE.
∵AB⊥BC，∴AB∥DE，又∵AE∥BC，
∴四边形ABDE是平行四边形，∴ED=AB=3.
8.【解析】在□ABCD中，AB∥CD，∴∠A+∠D=180°，又∵∠A=120°，
∴∠D=60°.
答案：60
9.【解析】因为平行四边形的对角线互相平分，所以OA=AC=7，OB=BD=4，又因为AB=10，所以△OAB的周长=7+4+10=21.
答案：21
10.【解析】∵平行四边形ABCD，∴ ( http: / / www.21cnjy.com )AD=BC，AB=CD，OB=OD，∵OE⊥BD，∴BE=DE，∵平行四边形ABCD的周长是20，∴2AB+2AD=20，∴AB+AD=10，∴△ABE的周长是AB+AE+BE=AB+AE+DE=AB+AD=10.
答案：10
11.【解析】∵四边形ABCD是平行四边形，
∴AD∥BC，BC=AD=3.
∴∠DAF=∠BFA.
∵AE平分∠DAB，
∴∠DAF=∠FAB.∴∠BFA=∠BAF.
∴AB=BF=BC+CF.
∴CF=AB-BC=5-3=2.
答案：2
12.【解析】本题主要考查点到直线的距离和平行线间的距离，①②③④⑤都正确.
答案：①②③④⑤
13.【解析】(1)3.
(2)①△ABE≌△CDF，
证明：在□ABCD中，AB∥CD，AB=CD，
∴∠ABE=∠CDF，
又∵BE=DF，∴△ABE≌△CDF(S.A.S.)；
②△ADE≌△CBF，
证明：在□ABCD中，AD∥BC，AD=BC，
∴∠ADE=∠CBF，
∵BE=DF，∴BD-BE=BD-DF，
即DE=BF，
∴△ADE≌△CBF(S.A.S.)；
③△ABD≌△CDB，
证明：在□ABCD中，AB=CD，AD=BC，
又∵BD=BD，∴△ABD≌△CDB(S.S.S.).
14.【证明】(1)∵AB∥CD，∴∠B=∠C.又∵AB=CD，BE=CF，
∴△ABE≌△DCF(S.A.S.).
(2)连结AF，DE，如图.
( http: / / www.21cnjy.com )
∵△ABE≌△DCF，∴AE=DF，
∠AEB=∠DFC.
∴∠AEF=∠DFE.∴AE∥DF.
∴四边形AFDE是平行四边形，即以点A，F，D，E为顶点的四边形是平行四边形.
15.【解析】(1)当AC旋转90°时，∠AOF=90°，
又∵AB⊥AC，∴∠BAC=90°，∴AB∥EF，
又∵四边形ABCD为平行四边形，∴AF∥BE，
∴四边形ABEF是平行四边形.
(2)∵四边形ABCD为平行四边形，
∴AO=CO，∠FAO=∠ECO，
又∵∠AOF=∠COE，∴△AOF≌△COE(A.S.A.)，
∴AF=CE，又∵AF∥CE，
∴四边形AFCE为平行四边形，∴AE=FC.
16.【解析】(1)∵CN∥AB，∴∠1=∠2.
在△AMD和△CMN中，
( http: / / www.21cnjy.com )
∴△AMD≌△CMN(A.S.A.)，∴AD=CN.
又AD∥CN，
∴四边形ADCN是平行四边形，∴CD=AN.
(2)∵AC⊥DN，∠CAN=30°，MN=1，
∴AN=2MN=2，
∴AM==，
∴S△AMN=AM·MN=××1=.
∵四边形ADCN是平行四边形，
∴S四边形ADCN=4S△AMN=2.
( http: / / www.21cnjy.com )