2023—2024学年人教版九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步练习(含答案)
文档属性
| 名称 | 2023—2024学年人教版九年级数学上册 24.2 点和圆、直线和圆的位置关系 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 110.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览



文档简介
24.2 点和圆、直线和圆的位置关系
一、选择题
1.直角三角形的外心在( )
A.直角顶点 B.直角三角形内
C.直角三角形外 D.斜边中点
2.圆的半径是6.5,如果圆心与直线的距离是4.5,那么直线和圆的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是( )
A.0<r<3 B.2<r<8 C.3<r<5 D.r>5
4.如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A.以PA为半径的圆 B.以PB为半径的
C.以PC为半径的圆 D.以PD为半径的圆
5.在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
A.点A在⊙C内 B.点A在⊙C上 C.点A在⊙C外 D.无法确定
6.如图,已知正方形,以点为圆心,长为半径作,点与的位置关系为( )
A.点在外 B.点在内 C.点在上 D.无法确定
7.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且,则等于( )
A. B. C. D.
8.如图,为的直径,与相切于点,交的延长线于点,且.若,则半径长为( )
A.2 B.3 C. D.
二、填空题
9.已知的半径为5,点到圆心的距离为8,则点在 (填“内”“上”或“外”).
10.平面上有及一点,点到上一点的距离最长为,最短为,则的半径为 .
11.如图,是的直径,点是外的一点,且是的切线,交于点,若,则 .
12.如图,已知的半径为1,点是外一点,且.若是的切线,为切点,连接,则 .
13.如图,ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,ABC的周长为14,则BC的长为 .
三、解答题
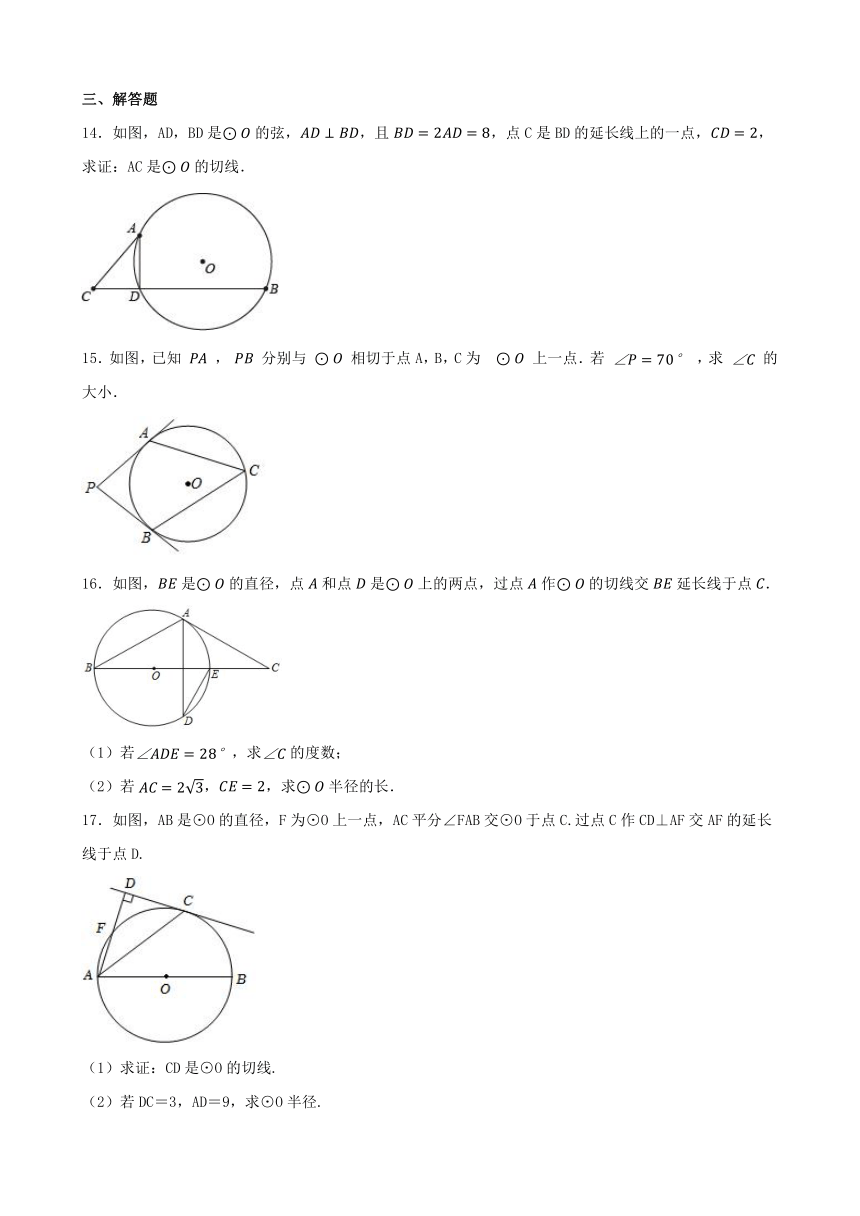
14.如图,AD,BD是的弦,,且,点C是BD的延长线上的一点,,求证:AC是的切线.
15.如图,已知 , 分别与 相切于点A,B,C为 上一点.若 ,求 的大小.
16.如图,是的直径,点和点是上的两点,过点作的切线交延长线于点.
(1)若,求的度数;
(2)若,,求半径的长.
17.如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线.
(2)若DC=3,AD=9,求⊙O半径.
参考答案
1.D
2.A
3.C
4.C
5.A
6.A
7.C
8.B
9.外
10.2或6
11.30°
12.
13.5
14.证明:连接AB,
∵,且
∴AB为直径,AB2=82+42=80,
∵CD=2,AD=4
∴AC2=22+42=20
∵CD=2,BD=8,
∴BC2=102=100
∴,
∴
∴AC是的切线.
15.解:连接OA、OB
∵ , 分别与 相切于点A,B,
∴∠OAP=∠OBP=90°,
∵
∴∠AOB=360°-∠OAP-∠OBP-∠P=110°
∴∠C= ∠AOB=55°.
16.(1)解:如图,连接 ,
,
,
切 于点 ,
,
在 中,
(2)解:设 ,
在 中,由勾股定理得: ,
即 ,
解得: ,
答: 半径的长是2.
17.(1)证明:连接OC,
∵AC平分∠FAB,
∴∠FAC=∠CAO,
∵AO=CO,
∴∠ACO=∠CAO,
∴∠FAC=∠ACO,
∴AD∥OC,
∵CD⊥AF,
∴CD⊥OC,
∵OC为半径,
∴CD是⊙O的切线;
(2)解:过点O作OE⊥AF于E,
∴AE=EF= ,∠OED=∠EDC=∠OCD=90°,
∴四边形OEDC为矩形,
∴CD=OE=3,DE=OC,
设⊙O的半径为r,则OA=OC=DE=r,
∴AE=9﹣r,
∵OA2﹣AE2=OE2,
∴r2﹣(9﹣r)2=32,
解得r=5.
∴⊙O半径为5.
一、选择题
1.直角三角形的外心在( )
A.直角顶点 B.直角三角形内
C.直角三角形外 D.斜边中点
2.圆的半径是6.5,如果圆心与直线的距离是4.5,那么直线和圆的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.若点A在⊙O内,点B在⊙O外,OA=3,OB=5,则⊙O的半径r的取值范围是( )
A.0<r<3 B.2<r<8 C.3<r<5 D.r>5
4.如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A.以PA为半径的圆 B.以PB为半径的
C.以PC为半径的圆 D.以PD为半径的圆
5.在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )
A.点A在⊙C内 B.点A在⊙C上 C.点A在⊙C外 D.无法确定
6.如图,已知正方形,以点为圆心,长为半径作,点与的位置关系为( )
A.点在外 B.点在内 C.点在上 D.无法确定
7.如图,PA、PB是⊙O的切线,A、B是切点,点C在⊙O上,且,则等于( )
A. B. C. D.
8.如图,为的直径,与相切于点,交的延长线于点,且.若,则半径长为( )
A.2 B.3 C. D.
二、填空题
9.已知的半径为5,点到圆心的距离为8,则点在 (填“内”“上”或“外”).
10.平面上有及一点,点到上一点的距离最长为,最短为,则的半径为 .
11.如图,是的直径,点是外的一点,且是的切线,交于点,若,则 .
12.如图,已知的半径为1,点是外一点,且.若是的切线,为切点,连接,则 .
13.如图,ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,ABC的周长为14,则BC的长为 .
三、解答题
14.如图,AD,BD是的弦,,且,点C是BD的延长线上的一点,,求证:AC是的切线.
15.如图,已知 , 分别与 相切于点A,B,C为 上一点.若 ,求 的大小.
16.如图,是的直径,点和点是上的两点,过点作的切线交延长线于点.
(1)若,求的度数;
(2)若,,求半径的长.
17.如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线.
(2)若DC=3,AD=9,求⊙O半径.
参考答案
1.D
2.A
3.C
4.C
5.A
6.A
7.C
8.B
9.外
10.2或6
11.30°
12.
13.5
14.证明:连接AB,
∵,且
∴AB为直径,AB2=82+42=80,
∵CD=2,AD=4
∴AC2=22+42=20
∵CD=2,BD=8,
∴BC2=102=100
∴,
∴
∴AC是的切线.
15.解:连接OA、OB
∵ , 分别与 相切于点A,B,
∴∠OAP=∠OBP=90°,
∵
∴∠AOB=360°-∠OAP-∠OBP-∠P=110°
∴∠C= ∠AOB=55°.
16.(1)解:如图,连接 ,
,
,
切 于点 ,
,
在 中,
(2)解:设 ,
在 中,由勾股定理得: ,
即 ,
解得: ,
答: 半径的长是2.
17.(1)证明:连接OC,
∵AC平分∠FAB,
∴∠FAC=∠CAO,
∵AO=CO,
∴∠ACO=∠CAO,
∴∠FAC=∠ACO,
∴AD∥OC,
∵CD⊥AF,
∴CD⊥OC,
∵OC为半径,
∴CD是⊙O的切线;
(2)解:过点O作OE⊥AF于E,
∴AE=EF= ,∠OED=∠EDC=∠OCD=90°,
∴四边形OEDC为矩形,
∴CD=OE=3,DE=OC,
设⊙O的半径为r,则OA=OC=DE=r,
∴AE=9﹣r,
∵OA2﹣AE2=OE2,
∴r2﹣(9﹣r)2=32,
解得r=5.
∴⊙O半径为5.
同课章节目录
