《新学案》2015年春高中数学苏教版必修5名师导学:第一章 解三角形(含解析)
文档属性
| 名称 | 《新学案》2015年春高中数学苏教版必修5名师导学:第一章 解三角形(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 684.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-20 00:00:00 | ||
图片预览




文档简介
第 1 章 解三角形
第1课时 正弦定理(1)
教学过程
一、 问题情境
1. 对于“即时体验”中的第2题:“在△ABC中,若C=75°,A=60°,b=,则这个三角形能确定吗 B,a,c能求出来吗 ”这个三角形虽然可以确定,但根据我们目前所掌握的知识还不能够求出a,c,这说明了什么呢 这只能说明我们对三角形中的边角之间的关系还缺乏足够的了解,还没有发现它们之间所隐含的规律.
2. 三角形中的边角之间究竟隐含着什么样的规律呢 还是让我们从特殊情况来考察:在Rt△ABC中,C=90°,试判定,与之间的大小关系.
二、 数学建构
问题1 对任意三角形,==也成立吗
用几何画板演示,如果不具备条件的话,也可以通过纸笔或计算器来计算任意三角形中三边长与其对角的正弦值之比,让学生通过验证感受到:对任意三角形,都有==
问题2 验证能代替证明吗
(验证不能代替证明,验证只是表明个别情形或特殊情形成立,还不能说明一般情形或任意情形都成立)
问题3 如何证明对任意三角形都有==成立呢
(根据教材P5中的途径提示,组织学生进行讨论,最好能由学生给出证明思路)
对于==这一关系的证明,我们一起来看下面的证法.
( http: / / www.21cnjy.com )
(图1)
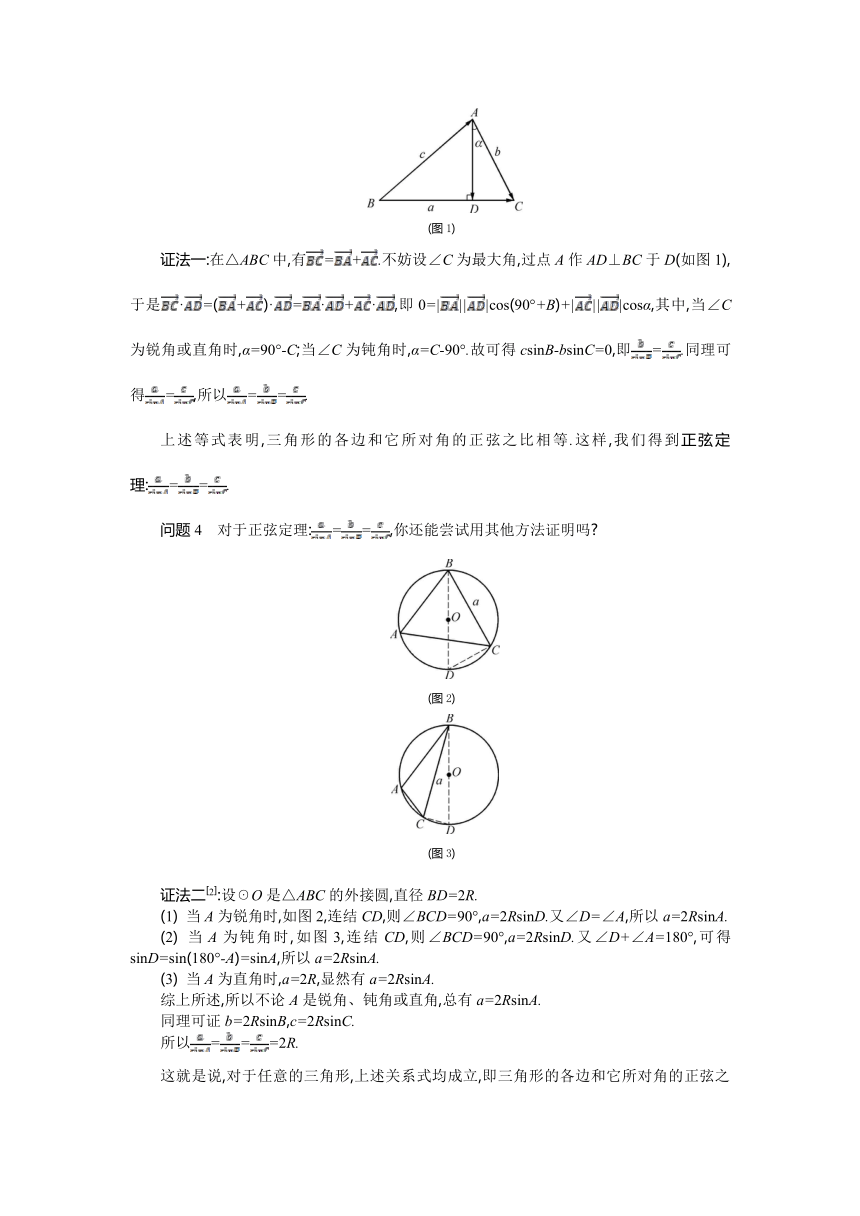
证法一:在△ABC中,有=+.不妨设∠C为最大角,过点A作AD⊥BC于D(如图1),于是·=(+)·=·+·,即0=||||cos(90°+B)+||||cosα,其中,当∠C为锐角或直角时,α=90°-C;当∠C为钝角时,α=C-90°.故可得csinB-bsinC=0,即=.同理可得=,所以==.
上述等式表明,三角形的各边和它所对角的正弦之比相等.这样,我们得到正弦定理:==.
问题4 对于正弦定理:==,你还能尝试用其他方法证明吗
( http: / / www.21cnjy.com )
(图2)
( http: / / www.21cnjy.com )
(图3)
证法二[2]:设☉O是△ABC的外接圆,直径BD=2R.
(1) 当A为锐角时,如图2,连结CD,则∠BCD=90°,a=2RsinD.又∠D=∠A,所以a=2RsinA.
(2) 当A为钝角时,如图3,连结CD, ( http: / / www.21cnjy.com )则∠BCD=90°,a=2RsinD.又∠D+∠A=180°,可得sinD=sin(180°-A)=sinA,所以a=2RsinA.
(3) 当A为直角时,a=2R,显然有a=2RsinA.
综上所述,所以不论A是锐角、钝角或直角,总有a=2RsinA.
同理可证b=2RsinB,c=2RsinC.
所以===2R.
这就是说,对于任意的三角形,上述关系式均成立,即三角形的各边和它所对角的正弦之比相等,因此,我们得到正弦定理:===2R.
正弦定理的变形:a=2RsinA,b=2R ( http: / / www.21cnjy.com )sinB,c=2RsinC(2R是△ABC外接圆的直径);a∶b∶c=sinA∶sinB∶sinC.
问题5 在课前预习时,“即时体验”中的第2题你解决了吗
三、 数学运用
【例1】 (教材P7例1)在△ABC中,A=30°,C=100°,a=10,求b,c.(精确到0.01)[3]
(见学生用书课堂本P1)
( http: / / www.21cnjy.com )
(例1)
[处理建议] (1) 先让学生自己动手作图 ( http: / / www.21cnjy.com ),看看此三角形是否确定,然后再考虑如何求B,b,c.(2) 理清解题思路:如图,直接应用正弦定理可求出边c;若求边b,则需通过三角形内角和为180°先求出角B,再利用正弦定理求出边b.
[规范板书] 解 B=180°-(A+C)=180°-(30°+100°)=50°.
因为==,所以b==≈15.32,c==≈19.70.
因此,b,c分别为15.32和19.70.
[题后反思] (1) 此类 ( http: / / www.21cnjy.com )问题结果为唯一解,学生较易掌握;如果已知两角和两角所夹的边去求其他边角,也是先利用内角和为180°求出第三角,再利用正弦定理求出其他边.(2) 因此,对“已知两角与任一边,求其他两边和一角”的问题都能够用正弦定理彻底解决,且解唯一.
变式 在△ABC中,已知A=60°,B=45°,c=3,求C,a,b.
[规范板书] 解 C=180°-(A+B)=180°-(60°+45°)=75°.因为==,所以a===,b===3-3.因此,C,a,b分别为75°,和3-3.
【例2】 根据下列条件解三角形:
(1) a=14,b=7,B=60°;
(2) c=,b=,B=45°.[4]
(见学生用书课堂本P2)
[处理建议] (1) 解三角形是指由六 ( http: / / www.21cnjy.com )个元素中的三个元素(至少有一个是边),求其余三个未知元素的过程;(2) 对于本题,先让学生讨论,尝试解答;然后教师在学生中交流,了解学生的思考过程,投影学生的求解过程,并纠正出现的错误.
[规范板书] 解 (1) ∵ a(2) 由正弦定理得sinC===,∴ C1=60°,或C2=180°-60°=120°.由于C2+B=120°+45°=165°<180°,故C2也符合要求.从而C有两解:C1=60°,或C2=120°.
当C1=60°时,A1=180°-(C1+B)=180°-(60°+45°)=75°,a1===1+;
当C2=120°时,A2=180°-(C2+B)=180°-(120°+45°)=15°,a2===1-.
[题后反思] (1) 同样是已知两边和一边的对角,但可能出现不同的结果,应向学生强调注意解题的灵活性.
(2) 对于第(1)题,如果没有考 ( http: / / www.21cnjy.com )虑到角A所受到的限制而求出角A的两个解,进而求出边a有两解,那么也可利用三角形两边之和大于第三边,两边之差小于第三边这一性质进行验证,进而排除不符题意的解.
(3) 思考:对于第(1)、(2)题,能否通过作图来分析为什么解的个数不一样 为什么第(2)题产生多解 (引导学生通过作出三角形来思考)
“已知两边和其中一边的对角,求另一边的对角”这类问题情形复杂,但若通过作图来考虑,情形就一目了然了.
① A为锐角:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
注意:当a② A为直角或钝角:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
变式 在△ABC中,已知c=5,A=45°,试判断当a分别取10,5,,时,角C的解的个数.
[规范板书] 解 (1) 当a=10时,有a>c,故角C有一解;
(2) 当a=5时,∵ csinA=5sin45°=5,∴ a=csinA,故角C有一解;
(3) 当a=时,有c>a>csinA=5sin45°=5,故角C有两解;
(4) 当a=时,有a变式 在△ABC中,证明:A>B sinA>sinB.
[处理建议] 先让学生分析得出条件与三角形的角有关,结论与三角形的角的正弦值有关.但是如何实现条件与结论的转化呢 自然联想到正弦定理.
[规范板书] 证明 因为a=2Rs ( http: / / www.21cnjy.com )inA,b=2RsinB,所以A>B a>b 2RsinA>2RsinB sinA>sinB,即A>B sinA>sinB.
[题后反思] (1) 不能利用正弦函数的单调 ( http: / / www.21cnjy.com )性进行证明,因为正弦函数在(0,π)内不具有单调性;(2) 在△ABC中,有A>B a>b sinA>sinB cosA四、 课堂练习
1. 在△ABC中,
(1) 已知A=30°,B=120°,b=8,求a;
(2) 已知A=45°,B=60°,c=,求b.[5]
解 (1) ∵ =,∴ a===.
(2) ∵ C=180°-(A+B)=180°-(45°+60°)=75°,=,∴ b===(-).
2. 根据下列条件解三角形:
(1) a=2,b=2,B=60°;
(2) a=,b=,B=45°.[6]
解 (1) ∵ =,∴ sinA===,∴ A1=30°,A2=150°.
当A1=30°时,C1=180°-(A1+B)=180°-(30°+60°)=90°,∴ c1===4;
当A2=150°时,A2+B=150°+60°>180°,故A2=150°应舍去(或者由a∴ A=30°,C=90°,c=4.
(2) ∵ =,∴ sinA===,∴ A1=60°,A2=120°.
当A1=60°时,C1=180°-(A1+B)=180°-(60°+45°)=75°,∴ c1===;
当A2=120°时,C2=180°-(A2+B)=180°-(120°+45°)=15°,∴ c2===.
∴ A=60°,C=75°,c=,或A=120°,C=15°,c=.
五、 课堂小结
1. 正弦定理及其变形形式:
(1) ===2R(2R是△ABC外接圆的直径);
(2) a=2RsinA,b=2RsinB,c=2RsinC,或a∶b∶c=sinA∶sinB∶sinC.
2. 利用正弦定理,可以解决以下两类有关三角形问题:
(1) 已知两角和任一边,求其他两边和一角;(这类问题由于两角已知,故第三角确定,三角形确定,解唯一,相对容易)
(2) 已知两边和其中一边的对角,求另一边的对角.(此类问题相对复杂些,要防止多解和少解的发生)
第2课时 正弦定理(2)
教学过程
一、 问题情境
问题1 你能举出在现实生活中哪些方面有可能会运用到解三角形的知识
问题2 你能举出在数学本身内部哪些方面有可能会运用到解三角形的知识
二、 数学运用
【例1】 (根据教材P9例 ( http: / / www.21cnjy.com )3改编)如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为15°的斜坡前进1000m后到达D处,又测得山顶B的仰角为75°,求山的高度BC.[2](见学生用书课堂本P3)
( http: / / www.21cnjy.com )
(例1)
[处理建议] (1) 让学生重新动手作图,从中理顺关系;(2) 要求BC,只要求出AB即可,因此考虑解△ABD.
[规范板书] 解 过点D作DE∥AC交BC于E,因为∠DAC=15°,所以∠ADE=165°,于是∠ADB=360°-165°-75°=120°.又∠BAD=45°-15°=30°,所以∠ABD=30°.在△ABD中,由正弦定理,得AB===1000(m).在Rt△ABC中,BC=AB·sin45°=1000×=500(m).
答:山的高度为500m.
[题后反思] (1) 此 ( http: / / www.21cnjy.com )题是正弦定理在高度测量问题中的应用,教学时应引导学生寻找和分析条件与结论所涉及的三角形中的边角关系;(2) 复杂的应用题,涉及的往往不止一个三角形,要在不同的三角形中求出需要的边和角,再在一个三角形中解决主要问题,这就需要我们处理问题要有先后次序、条理清晰、目标明确.
变式 一货轮航行到M处,测得灯塔S在货 ( http: / / www.21cnjy.com )轮的北偏东15°相距20n mile处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔S在货轮的北偏东45°方向上,求货轮的航行速度.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 设货轮的航行速度为vnmile/h,如图,在△MNS中,MS=20n mile,MN=v,∠NMS=30°+15°=45°,∠MNS=180°-30°-45°=105°,从而∠MSN=30°.由正弦定理得=,即=,所以v=20(-)(nmile/h).
【例2】 已知△ABC,证明:a=bcosC+ccosB(射影定理).[3] (见学生用书课堂本P4)
[处理建议] 让学生回顾教材P56中正弦定理的证法一,进而使他们从中受到启发.
[规范板书] 证明 由正弦定理得a=2 ( http: / / www.21cnjy.com )RsinA,b=2RsinB,c=2RsinC,所以bcosC+ccosB=2RsinBcosC+2RsinCcosB=2Rsin(B+C)=2Rsin(180°-A)=2RsinA=a,所以a=bcosC+ccosB.
[题后反思] (1) 三角形中的三 ( http: / / www.21cnjy.com )角恒等式的证明,通常采用的方法是边角归一,即转化为边,或转化为角的单一的形式来证明;(2) 实现边角归一的工具是正(余)弦定理;(3) 要在解题的实践中不断积累这类题的解题方法.
变式 (教材P10例5) 在△ABC中,AD是∠BAC的平分线(如图),证明:=.(内角平分线定理)
( http: / / www.21cnjy.com )
(变式)
[规范板书] 证明 设∠BAD=α,∠BDA=β,则∠CAD=α,∠CDA=180°-β.在△ABD和△ACD中分别运用正弦定理,得=,==,所以=,即=.
*【例3】 在△ABC中,已知acosA=bcosB,试判断△ABC的形状.[4]
[处理建议] (1) 让学生回忆:特殊三角形有哪些 它们又是如何定义的 (2) 启发学生从角或边考虑,寻求解题途径.
[规范板书] 解 acosA=bcosB ( http: / / www.21cnjy.com ) 2RsinAcosA=2RsinBcosB Rsin2A=Rsin2B sin2A=sin2B 2A=2B或2A+2B=180°,即有A=B或A+B=90°,从而有A=B或C=90°.所以,此三角形为等腰三角形或直角三角形.
[题后反思] (1) 此题是关于三角 ( http: / / www.21cnjy.com )形的形状判断的问题,判断三角形的形状,通常是指等腰三角形、等边三角形、直角三角形或等腰直角三角形等特殊三角形;(2) 此类问题,主要是借助于正(余)弦定理,将三角形中边的关系与角的关系相互转化:一方面可以转化为边的关系来判断;另一方面可以转化为角的关系来判断.此题是转化为角来判断的,学过余弦定理后,此题也可以转化为边来判断;(3) 防止遗漏2A+2B=180°的发生.
变式 (教材P9例4)在△ABC中,已知==,试判断△ABC的形状.
[规范板书] 解 == == == tanA=tanB=tanC.又A,B,C∈(0,π),所以A=B=C,从而△ABC为正三角形.
三、 课堂练习
1. 海上有相距10n mile的A,B两个小岛,从A岛望B岛和C岛成60°角(即∠BAC=60°),从C岛望B岛和A岛成45°角(即∠ACB=45°),则B,C两岛之间的距离是5n mile.
提示 由正弦定理得BC===5(n mile).
2. 在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=1∶∶2.
提示 由A∶B∶C=1∶2∶3及A+B+C=180°,可求得A=30°,B=60°,C=90°.从而a∶b∶c=sinA∶sinB∶sinC=sin30°∶sin60°∶sin90°=1∶∶2.
3. 在△ABC中,已知b=2csinB,求角C.
解 由b=2csinB,得2RsinB=2×2RsinCsinB,即sinB(1-2sinC)=0.因为sinB≠0,所以sinC=.又C∈(0,π),因此C=或.
4. 在△ABC中,已知==,判断△ABC的形状.
解 由正弦定理得==,所以tanB=tanC=1.又B,C∈(0,π),所以B=C=,从而A=.因此,△ABC为等腰直角三角形.
四、 课堂小结
通过本节课的学习,了解到正弦定理的应用主要体现在以下几个方面:
(1) 求三角形中的基本元素;
(2) 三角形中恒等式的证明;
(3) 判断三角形的形状:
给出三角形中的三角关系式,判断三角形的形状,通常有两种方法:① 统一化为角,再判断;② 统一化为边,再判断.
此外,在三角形中,对于恒等式的证明和三角形形状的判断这两类问题,尤其要注意正弦定理的变形形式的使用.
第3课时 余弦定理(1)
教学过程
一、 问题情境
1. 在前面我们通过研究发现了正弦定 ( http: / / www.21cnjy.com )理,并运用正弦定理解决了三角形中的两类问题.当两边夹一角或三条边确定了,这个三角形就确定了,其余的边和角也就确定了,但我们无法用正弦定理求出其余的边和角,这说明了什么呢 这只能说明我们对三角形的探究还不够深入,三角形中的边角关系我们还没有完全掌握,接下来我们该怎么办呢
2. 在上节课中,我们通过等式=+的两边与(AD为△ABC中BC边上的高)作数量积,将向量等式转化为数量关系,进而推出了正弦定理.具体是如何操作的,你还有印象吗
二、 数学建构
问题1 还有其他途径将向量等式=+数量化吗
(,,这三个向量的模与三角形的边长有关,它们的夹角与三角形的角有关,引导学生分析出:两边平方)
·=(+)·(+)
=+2·+
=||2+2||||cos(π-A)+||2
=c2-2cbcosA+b2,
即a2=b2+c2-2bccosA.
同理可得b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
上述等式表明,三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.这样我们就得到余弦定理:
余弦定理(形式一):a2=b2+c2-2bccosA,
b2=c2+a2-2cacosB,
c2=a2+b2-2abcosC.
问题2 回顾正弦定理不同的证明方法,你还能尝试用其他方法证明余弦定理吗
(引导学生回顾通过建立平面直角坐标系,利用三角函数的定义证明正弦定理的方法,对照余弦定理的特点,产生如下证法)
证明:建立如图1所示的平面直角坐标系,则A(0,0),B(ccosA,csinA),C(b,0).
( http: / / www.21cnjy.com )
(图1)
所以a2=(ccosA-b)2+(csinA)2
=c2cos2A+c2sin2A-2bccosA+b2
=b2+c2-2bccosA.
同理可得b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
(此证明方法的优点在于不必对角A进行锐角、直角、钝角等分类讨论)
余弦定理也可以写成如下形式:
余弦定理(形式二):cosA=,cosB=,cosC=.
问题3 余弦定理a2=b2+c2-2bccosA这种形式能帮助我们解决正弦定理不能解决的什么问题
(引导学生分析等式左右两边的特 ( http: / / www.21cnjy.com )点:右边涉及两边及其夹角,而左边涉到夹角的对边.即已知两边和它们的夹角,利用这种形式的余弦定理可求出第三边,进而求出其他两个角)
问题4 余弦定理cosA=这种形式能帮助我们解决正弦定理不能解决的什么问题
(引导学生分析等式左右两边的特点:右边 ( http: / / www.21cnjy.com )涉及三边,而左边涉及一角.即已知三边,利用这种形式的余弦定理可求出三个角.这样,问题3、问题4对于正弦定理不能解决的两类遗留问题应用余弦定理就能彻底解决了)
三、 数学运用
在证明了余弦定理之后,我们来进一步学习余弦定理的应用.
利用余弦定理,可以解决以下两类有关三角形的问题:
(1) 已知三边,求三个角;(这类问题由于三边确定,故三角也确定,解唯一)
(2) 已知两边和它们的夹角,求第三边和其 ( http: / / www.21cnjy.com )他两个角.(这类问题第三边是确定的,因而其他两个角唯一,故解唯一;不会产生类似利用正弦定理解三角形时所产生的判断取舍等问题)
接下来,我们通过例题进一步体会与总结.
【例1】 (根据教材P14例1改编)在△ABC中,
(1) 已知b=8,c=3,A=60°,求a;
(2) 已知a=2,b=,c=+1,求A.[2]
(见学生用书课堂本P5)
[处理建议] (1) 第一小 ( http: / / www.21cnjy.com )题属于已知两边及夹角求边的类型,可通过余弦定理形式一求出第三边;第二小题属于已知三角形三边求角的类型,可以利用余弦定理形式二求出角;(2) 这两小题是余弦定理直接简单的应用,可以让学生板演,培养学生的计算能力.
[规范板书] 解 (1) 由a2=b2+c2-2bccosA,得
a2=82+32-2×8×3×cos60°=49,∴ a=7.
(2) 由cosA=,得
cosA==,∴ A=45°.
[题后反思] (1) 若将例1的要求改为解三角形,那么后继问题又该怎样解决呢
(2) 对于已知两边及夹角解三角形的类 ( http: / / www.21cnjy.com )型,可通过余弦定理形式一先求出第三边,在第三边求出后,其余两角求解有两种思路:一是利用余弦定理形式二根据三边求第二个角,第三个角用三角形内角和定理求出;二是利用正弦定理根据两边及一边对角求解(但若用正弦定理求解,需对两种结果进行判断取舍,而在0°180°内,余弦有唯一解,故用余弦定理较好).
(3) 在解三角形时,如果正弦定理与余弦定理均可选用,那么求边用两个定理均可,求角用余弦定理则可免去判断取舍的麻烦.
【例2】 (教材P14例3)证明:在△ABC中,当∠C为锐角时,a2+b2>c2;当∠C为钝角时,a2+b2(见学生用书课堂本P6)
[处理建议] 条件是角,结论是边,而且还涉及三条边,自然会想到用余弦定理.
[规范板书] 证明 当∠C为锐角时,cosC>0,由余弦定理得cosC=>0,即a2+b2-c2>0,所以a2+b2>c2.
同理可证,当∠C为钝角时,a2+b2[题后反思] 当∠C为直角时,则cosC=0,所以a2+b2=c2.因此,余弦定理可以看做是勾股定理的推广.
变式 钝角△ABC的三边的长为连续的自然数,求三边的长.
[规范板书] 解 不妨设a=n,b=n+1,c=n+2(n∈N*),则角C为最大角且为钝角.
∴ cosC=<0,∴ a2+b2-c2<0,∴ a2+b2所以三边的长分别为2,3,4.
*【例3】 在△ABC中,已知a=8,b=7,B=60°,求c及S△ABC.[4]
[处理建议] (1) 思路一:根据已知条件可以先由正弦定理求出角A,再结合三角形内角和定理求出角C,再利用正弦定理求出边c,而三角形面积由公式S△ABC=acsinB可以求出.(2) 思路二:若用余弦定理求c,表面上缺少角C,但可利用余弦定理b2=c2+a2-2cacosB建立关于c的方程,也能达到求c的目的.
[规范板书] 解法一 由正弦定理得=,∴ sinA=.∵ a>b,∴ A>B=60°,∴ A有两解,∴ A1≈81.8°,A2≈98.2°.∴ C1=38.2°,C2=21.8°.由=,得c1=5,c2=3.∴ S△ABC=ac1sinB=10或S△ABC=ac2sinB=6.
解法二 由余弦定理得72=c2+82-2×8·c·cos60°,整理得c2-8c+15=0,解得c1=5,c2=3.∴ S△ABC=ac1sinB=10或S△ABC=ac2sinB=6.
[题后反思] (1) 在解法一中,注意 ( http: / / www.21cnjy.com )利用正弦定理应有两种结果,避免遗漏;而解法二更有耐人寻味之处,体现出余弦定理作为公式而直接应用的另外用处,即可以用之建立方程,从而运用方程的观点去解决问题,故解法二应引起学生的注意.
(2) 通过上述例题,可要求学生总结余弦 ( http: / / www.21cnjy.com )定理在求解三角形时的适用范围(已知三边求任意角或已知两边及夹角解三角形),同时注意余弦定理在求角时的优势以及利用余弦定理建立方程的解法.
变式 在△ABC中,已知a=7,c=5,A=120°,求的值.
[规范板书] 解 由余弦定理得72=b2+52-2×5·b·cos120°,整理得b2+5b-24=0,解得b1=3,b2=-8(舍去).所以==.
四、 课堂练习
1. 在△ABC中,
(1) 若a=20,b=29,c=21,则B=90°;
(2) 若a=3,c=2,B=150°,则b=7.[5]
提示 (1) ∵ cosB===0,∴ B=90°.
(2) ∵ b2=c2+a2-2cacosB=22+(3)2-2×2×3×=49,∴ b=7.
2. 若三条线段的长分别为5,6,7,则用这三条线段构成的三角形中最大角的正弦值为.
提示 不妨设在构成的△ABC中,a=5,b=6,c=7,对应的角分别为A,B,C,则最大的角为C.∵ cosC===,∴ sinC=.
3. 在△ABC中,若a2=b2+c2+bc,则A=120°.
提示 ∵ cosA=
==-,∴ A=120°.
五、 课堂小结
通过本节课的学习,我们一起研究了余弦定理的证 ( http: / / www.21cnjy.com )明方法,同时又进一步了解了向量的工具性作用,并且明确了利用余弦定理可以解决以下两类有关三角形的问题:
(1) 已知三边,求三个角;(这类问题由于三边确定,所以三角也确定,故解唯一)
(2) 已知两边和它们的夹角,求第三 ( http: / / www.21cnjy.com )边和其他两个角.(这类问题第三边是确定的,因而其他两个角唯一,故解唯一;不会产生类似利用正弦定理解三角形时所产生的判断取舍等问题)
第4课时 余弦定理(2)
教学过程
一、 问题情境
1. 你能举出在现实生活中与解三角形有关,但又是正弦定理所解决不了的例子吗
2. 你能举出在数学本身内部哪些方面有可能会运用到余弦定理知识的例子吗
二、 数学运用
( http: / / www.21cnjy.com )
(例1)
【例1】 如图,甲船以30n mile/h的速度向正北方向航行,乙船按某固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船北偏西105°方向的B1处,此时两船相距20n mile;当甲船航行20min到达A2处时,乙船航行到甲船北偏西120°方向的B2处,此时两船相距10n mile.问:乙船每小时航行多少海里 [2]
(见学生用书课堂本P7)
[处理建议] (1) 让学生读懂题意,帮助学生正确构造三角形是关键;(2) 让学生自己结合题设条件、正弦定理或余弦定理求解.
[规范板书] 解 如图1,连结A1B2,由已知得A2B2=10,A1A2=30×=10,∴ A1A2=A2B2.又∠A1A2B2=180°-120°=60°,∴ △A1A2B2是等边三角形,∴ A1B2=A1A2=10.由已知得A1B1=20,∠B1A1B2=105°-60°=45°.
( http: / / www.21cnjy.com )
(图1)
在△A1B2B1中,由余弦定理得B1=A1+A1-2A1B1·A1B2·cos45°=202+(10)2-2×20×10×=200,∴ B1B2=10.因此,乙船的速度为×60=30(n mile/h).
答:乙船每小时航行30n mile.
变式 如图2,若连结A2B1,此题又如何求解呢
( http: / / www.21cnjy.com )
(图2)
[规范板书] 解 如图2,连结A2B1,由已知得A1B1=20,A1A2=30×=10,∠B1A1A2=105°.
在△A2A1B1中,由余弦定理得A2=A1+A1-2A1B1·A1A2·cos105°=(10)2+202-2×10×20×=100(4+2),∴ A2B1=10(1+).
由正弦定理得sin∠A1A2B1=·sin∠B1A1A2=·=,∴ ∠A1A2B1=45°,则∠B1A2B2=60°-45°=15°.
在△B1A2B2中,A2B2=10,由余弦定理得B1=A2+A2-2A2B1·A2B2·cos15°=[10(1+)]2+(10)2-2×10(1+)×10×=200,∴ B1B2=10.因此,乙船的速度为×60=30(n mile/h).
答:乙船每小时航行30n mile.
[题后反思] 变式的解法也是构造三角形的一种方法,但计算量大,通过比较,要让学生善于利用条件优化解题过程.
【例2】 在△ABC中,已知acosB=bcosA,试判断△ABC的形状.[3] (见学生用书课堂本P8)
[处理建议] 对于三角形形状的判断,可 ( http: / / www.21cnjy.com )以根据角的关系,也可以根据边的关系,所以在已知条件的运用上,可以考虑两种途径:① 将边转化为角;② 将角转化为边.让学生从这两个角度进行分析.
[规范板书] 解法一 (利用余弦定理化角为边)acosB=bcosA a·=b· c2+a2-b2=b2+c2-a2,∴ 2a2=2b2,即a=b.故此三角形是等腰三角形.
解法二 (利用正弦定理化边为角)acos ( http: / / www.21cnjy.com )B=bcosA 2RsinAcosB=2RsinBcosA,∴ sinAcosB-cosAsinB=0,∴ sin(A-B)=0(亦可变到tanA=tanB).∵ -π[题后反思] (1) 在判定三角形 ( http: / / www.21cnjy.com )形状时,一般考虑从两个方向进行变形,一个方向是边,走代数变形之路,通常是正、余弦定理结合使用;另一个方向是角,走三角变形之路,通常是运用正弦定理,要求学生注重边角转化的桥梁——正(余)弦定理.(2) 走三角变形之路,就要熟练掌握三角公式,应注意在根据三角函数值求角时,一定要先确定角的范围.
变式 在△ABC中,已知2cosBsinA=sinC,试判断△ABC的形状.
[规范板书] 解法一 2cosBsinA=sinC 2cosBsinA=sin[π-(A+B)] 2cosBsinA=sin(A+B) 2cosBsinA=sinAcosB+cosAsinB cosBsinA=cosAsinB = tanA=tanB.
又A,B∈(0,π),所以A=B.因此,△ABC为等腰三角形.
解法二 由正、余弦定理得2cosBsinA=sinC 2··= c2+a2-b2=c2 a2=b2 a=b.因此,△ABC为等腰三角形.
【例3】 (根据教材P16例6改编)在 ABCD中,证明:AC2+BD2=2(AB2+AD2).[4]
( http: / / www.21cnjy.com )
(例3)
(见学生用书课堂本P8)
[处理建议] (1) 利用正(余)弦 ( http: / / www.21cnjy.com )定理的前提是必须在三角形中,在四边形中如何选择有用的三角形是关键;(2) 任何一个三角形都不可能包含四边,因此必须选择两个三角形,让学生按此思路,往下思考.
[规范板书] 证明 设∠ABC=α,∠ ( http: / / www.21cnjy.com )BCD=π-α.在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BC·cosα ①.在△BCD中,由余弦定理得BD2=CD2+BC2-2CD·BC·cos(π-α) ②.因为cos(π-α)=-cosα,CD=AB,BC=AD,将①②两式相加得AC2+BD2=2(AB2+AD2).
[题后反思] 几何证明的关键是把有关量放到三角形中,借助正(余)弦定理,建立它们的关系,从而达到证明的效果,其中构造三角形是关键.
( http: / / www.21cnjy.com )
(变式)
变式 (教材P16例6)如图,若AM是△ABC中BC边上的中线,求证:AM=.
[规范板书] 证明 设∠AMB=α,则∠AMC=180°-α.在△ABM中,由余弦定理,得AB2=AM2+BM2-2AM·BMcosα.在△ACM中,由余弦定理,得AC2=AM2+MC2-2AM·MCcos(180°-α).因为cos(180°-α)=-cosα,BM=MC=BC,所以AB2+AC2=2AM2+BC2,因此,AM=.
*【例4】 在△ABC中,求证:a2sin2B+b2sin2A=2absinC.[5]
[处理建议] 此题所证结论包 ( http: / / www.21cnjy.com )含△ABC的边角关系,证明时可以考虑两种途径:一是把角的关系通过正、余弦定理转化为边的关系;二是把边的关系转化为角的关系,一般是通过正弦定理.让一部分学生走“化为边”这一途径,让另一部分学生走“化为角”这一途径.
[规范板书] 证法一 (化 ( http: / / www.21cnjy.com )边为角)a2sin2B+b2sin2A=(2RsinA)22sinB·cosB+(2RsinB)22sinA·cosA=8R2sinA·sinB(sinAcosB+cosAsinB)=8R2sinAsinBsinC=2·2RsinA·2RsinB·sinC=2absinC.所以原式得证.
证法二 (化角为边)左边=a2·2sinBcosB+b2·2sinAcosA=a2··+b2··=(a2+c2-b2+b2+c2-a2)=·2c2==2ab·=2absinC=右边.所以原式得证.
[题后反思] (1) 由边向角转化,通常利 ( http: / / www.21cnjy.com )用正弦定理的变形形式(a=2RsinA,b=2RsinB,c=2RsinC),在转化为角的关系式后,要注意三角函数公式的运用,在此题证明过程中用到了正弦二倍角公式sin2A=2sinAcosA,正弦两角和公式sin(A+B)=sinAcosB+cosAsinB;由角向边转化,要结合正弦定理变形形式以及余弦定理形式二.
(2) 三角形中的有关证明问题,主要是围绕三角形的边和角的三角函数展开,从某种意义上来看,这类问题就是有了目标的含边和角的式子的化简问题.
变式 已知△ABC,请用余弦定理证明:a=bcosC+ccosB.
[规范板书] 证明 bcosC+ccosB=b·+c·===a,即有a=bcosC+ccosB.
四、 课堂练习
1. 在 ABCD中,已知B=120°,AB=6,BC=4,则AC=2,BD=2.
提示 由余弦定理得AC2=AB2+BC2-2·AB·BC·cosB=62+42-2×6×4×cos120°=76,∴ AC=2.由余弦定理得BD2=AD2+AB2-2·AD·AB·cosA=42+62-2×4×6×cos60°=28,∴ BD=2.
2. 在△ABC中,证明:b=ccosA+acosC.(请你尝试用两种不同方法证明)
证法一 ccosA+acosC=2RsinC ( http: / / www.21cnjy.com )cosA+2RsinAcosC=2Rsin(A+C)=2Rsin(π-B)=2RsinB=b,即b=ccosA+acosC.
证法二 ccosA+acosC=c·+a·==b,即证.
3. 在△ABC中,已知a,b是方程x2-2x+2=0的两个根,且2cos(A+B)=-1,求c.
解 ∵ 2cos(A+B)=-1,∴ cos(A+B)=-,而0五、 课堂小结
1. 我们熟悉了正、余弦定理在进行边角关系转换时的桥梁作用,并利用了正、余弦定理对三角恒等式进行证明以及对三角形形状进行判断.
2. 我们要体会正、余弦定理的边角转换功能,注意常见解题方法与解题技巧的总结,不断提高三角形问题的求解能力.
第5课时 正弦定理、余弦定理的应用(1)
教学过程
一、 问题情境
问题 复习前两节的例题、练习、习题,总结一下:正弦定理、余弦定理能解决实际中的哪些问题
(正弦定理、余弦定理体现了三角形中边角之间的 ( http: / / www.21cnjy.com )相互关系,在测量、航海、几何、物理学等方面都有非常广泛的应用.下面,我们将举例来说明解三角形在实际中的一些应用)
二、 数学建构
正弦定理:===2R;
a=2RsinA,b=2RsinB,c=2RsinC;
a∶b∶c=sinA∶sinB∶sinC.
余弦定理:a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC;
cosA=,cosB=,cosC=.
三、 数学运用
【例1】 如图,位于A处的信 ( http: / / www.21cnjy.com )息中心获悉:在其正东方向相距40n mile的B处有一艘渔船遇险,正在原地等待营救.信息中心立即把这一消息告知在其南偏西30°方向、相距20n mile的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cosθ的值.[2] (见学生用书课堂本P9)
( http: / / www.21cnjy.com )
(例1)
[处理建议] 思路解析:本例考查 ( http: / / www.21cnjy.com )了正弦定理、余弦定理的建模应用.如图,确定θ,关键是确定∠ACB,于是问题转化为求△ABC中的∠ACB,应用问题就转化为解三角形问题.
[规范板书] 解 连接BC,在△ABC中,AB=40,AC=20,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=402+202+2×40×20×=2800,∴ BC=20.由正弦定理得sin∠ACB===.由∠BAC=120°,知∠ACB为锐角,则cos∠ACB=.由θ=∠ACB+30°,得cosθ=cos(∠ACB+30°)=cos∠ACBcos30°-sin∠ACBsin30°=.
[题后反思] (1) 熟练掌握正、余弦定理 ( http: / / www.21cnjy.com )的应用;(2) 测量角度,首先应明确方位角、方向角等含义;(3) 在解应用题时,首先分析题意,分清已知与所求,再根据题意正确画出示意图;(4) 解题时要注意体会正弦定理、余弦定理“联袂”使用的优点,同时注意三角函数知识在求解过程中的应用.
变式 一船自西向东匀速航行,上午10时 ( http: / / www.21cnjy.com )到达一座灯塔P南偏西75°的方向、距塔68n mile的M处,下午2时到达这座灯塔东南方向的N处,求这只船的航行速度.
(变式)
[规范板书] 解 如图,在△PMN中,由正弦定理得MN===34,∴ v==(n mile/h).即这只船的航行速度为n mile/h.
【例2】 在海岸A处,发现北偏东45°方向、距离A处(-1)n mile的B处有一艘走私船,若在A处北偏西75°方向、距离A处2n mile的C处的缉私船奉命以10n mile/h的速度追截走私船,此时,走私船正以10n mile/h的速度从B处向北偏东30°的方向逃跑,问:缉私船沿什么方向能最快追上走私船 [3]
(见学生用书课堂本P10)
[处理建议] 思路解析:本例考查了 ( http: / / www.21cnjy.com )正弦定理、余弦定理的建模应用.如图,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求出∠BCD.
[规范板书] 解 设缉私船用了th在D处追上走私船(如图),则有CD=10t,BD=10t.在△ABC中,AB=-1,AC=2,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=22+-2×2×(-1)×cos120°=6,∴ BC=.
( http: / / www.21cnjy.com )
(例2)
由正弦定理得sin∠ABC===,∴ ∠ABC=45°,∴ BC与正北方向垂直.
在△BCD中,∠CBD=90°+30°=120°,由正弦定理得sin∠BCD===,∴ ∠BCD=30°.∴ 缉私船沿北偏东60°的方向能最快追上走私船.
[题后反思] (1) 测量角度, ( http: / / www.21cnjy.com )首先应明确方位角、方向角等含义;(2) 在解应用题时,首先分析题意,分清已知与所求,再根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题时要注意体会正弦定理、余弦定理“联袂”使用的优点.
变式 如图,已知两座灯塔A和B与海洋观 ( http: / / www.21cnjy.com )察站C的距离相等,灯塔A在观察站C北偏东40°的方向上,灯塔B在观察站C南偏东60°的方向上,则灯塔A在灯塔B北偏西多少度的方向上
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 由已知得∠ACB ( http: / / www.21cnjy.com )=180°-40°-60°=80°,又AC=BC,∴ ∠A=∠ABC=50°,∠ABD=∠CBD-∠ABC=60°-50°=10°.∴ 灯塔A在灯塔B北偏西10°的方向上.
*【例3】 用同样高度的两个测角仪A ( http: / / www.21cnjy.com )B和CD分别测得正西方向上空的气球E的仰角是α和β.已知B,D间的距离为a,测角仪的高度是b,求气球的高度.[4]
( http: / / www.21cnjy.com )
(例3)
[处理建议] 在Rt△EGA中求解EG ( http: / / www.21cnjy.com ),只有角α一个条件,需要再有一边长被确定,而△EAC中有较多已知条件,故可在△EAC中考虑EA边长的求解,而在△EAC中有角β,∠EAC=180°-α与边AC=a,故可以利用正弦定理求解EA.
[规范板书] 解 在△ACE中,AC=BD=a,∠ACE=β,∠AEC=α-β,由正弦定理得AE==.
在Rt△AGE中,EG=AE·sinα=.
∴ EF=FG+GE=b+.
答:气球的高度是b+.
[题后反思] (1) 在 ( http: / / www.21cnjy.com )测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内视线与水平线的夹角;(2) 准确理解题意,分清已知与所求,画出示意图;(3) 运用正(余)弦定理,有序地解相关的三角形,逐步求解问题的答案,注意等价转化思想的运用.
变式 你还能用其他方法求出气球的高度吗
[处理建议] 本题也可以通过解两个直角三角形来解决,思路如下:设EG=x,在Rt△EGA中,利用表示AG;在Rt△EGC中,利用表示CG,而CG-AG=CA=a,故可以求出EG,从而求出气球的高度EF.
四、 课堂练习
1. 设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sinA=5sinB,则角C=120°.
2. 地上画了一个角,即∠BDA ( http: / / www.21cnjy.com )=60°.某人从角的顶点D出发,沿角的一边DA行走10m后,拐弯往另一方向行走14m正好到达∠BDA的另一边BD上的一点,我们将该点记为E,则E与D之间的距离为16m.
提示 如图,设ED=xm ( http: / / www.21cnjy.com ),则由余弦定理得142=102+x2-2x·10cos60°,整理得x2-10x-96=0,解得x=16或x=-6(舍去).所以E与D之间的距离为16m.
( http: / / www.21cnjy.com )
(第2题)
3. 江岸边有一炮台高30m,江中 ( http: / / www.21cnjy.com )有两条船,由炮台顶部测得两船的俯角分别为45°和30°,若这两条船与炮台底部连线成30°角,则两条船相距30m.
提示 设炮台顶部为C,底部为O,两条船分别为A,B,在Rt△AOC与Rt△BOC中,OA=OC·tan45°=30×1=30,OB=OC·tan60°=30×=30.
在△OAB中,由余弦定理得AB2=OA2+OB2-2OA·OB·cos∠AOB=302+-2×30×30×cos30°=900,∴ AB=30.∴ 两条船相距30m.
五、 课堂小结
1. 通过本节课的学习,我们知 ( http: / / www.21cnjy.com )道正弦定理、余弦定理有着非常广泛的应用.如果我们抽去每个应用题中与生产、生活实际所联系的外壳,就暴露出解三角形问题的本质,这就需要我们在解决实际问题的过程中,不断提高分析问题和解决问题的能力,以及将实际问题转化为抽象的数学问题的能力.
2. 理解各种应用问题中的有关名词、术语,如坡度、俯角、仰角、方向角、方位角等.
第6课时 正弦定理、余弦定理的应用(2)
教学过程
一、 数学运用
在上一节课中,我们一起学习了正、余 ( http: / / www.21cnjy.com )弦定理在实际中的应用,了解了一些把实际问题转化为解三角形问题的方法,掌握了一定的解题方法与技巧;在这一节课中,我们将给出几个例题,请大家尝试用上一节课所学的方法加以解决.
【例1】 如图,为了测量河 ( http: / / www.21cnjy.com )对岸A,B两点间的距离,在所站这一岸定一基线CD,现已测出CD=a,∠ACD=α,∠BCD=β,∠BDC=γ,∠ADC=δ,试求AB的长.[2]
( http: / / www.21cnjy.com )
(例1)
(见学生用书课堂本P11)
[处理建议] (1) 先帮助学 ( http: / / www.21cnjy.com )生分析思路,然后让学生解决;(2) 如图,对于AB的求解,可以在△ABC中或者△ABD中求.若在△ABC中求解,由∠ACB=α-β,故需先求出AC,BC,再利用余弦定理求得,而AC可在△ACD中利用正弦定理求得,BC可在△BCD中利用正弦定理求得.
[规范板书] 解 在△ACD中,由正弦定理得AC===.
在△BCD中,由正弦定理得BC===.
在△ABC中,∠ACB=α-β,由余弦定理得AB=
.
[题后反思] (1) 熟练掌握正、余弦定理的应用;(2) 注意体会例1的求解过程在实际中的应用.
变式 直线AB外有一点C,∠ABC=60°, ( http: / / www.21cnjy.com )AB=200km,汽车甲以80km/h的速度由A向B行驶,同时摩托车乙以50km/h的速度由B向C行驶,问:运动开始几小时后,两车的距离最小
[规范板书] 解 设经过th后,两车相距skm,则由余弦定理得s2=(200-80t)2+(50t)2-2×(200-80t)×(50t)·cos60°=12900t2-42000t+40000.当t=≈1.6时,s最小.
答:运动开始约1.6h后,两车的距离最小.
【例2】 据气象台预报,距S岛正东方 ( http: / / www.21cnjy.com )向300km的A处有一台风中心形成,并正以30km/h的速度沿北偏西30°的方向移动,在距台风中心270km以内的地区将受到台风的影响.问:S岛是否受到台风影响 若受到影响,从现在起经过多少小时S岛开始受到台风的影响 持续时间多久 [3]
(见学生用书课堂本P12)
[处理建议] (1) 先 ( http: / / www.21cnjy.com )帮助学生分析思路,然后让学生解决;(2) 设B为台风中心,则B为AB边上的动点,SB也随之变化.S岛是否受台风影响可转化为SB≤270这一不等式是否有解的判断,则需表示出SB,可设台风中心经过th到达B点,则在△ABS中,由余弦定理可求出SB.
[规范板书] 解 设台风中心经过th到达B点,由题意得∠SAB=90°-30°=60°.
( http: / / www.21cnjy.com )
(例2)
在△ABS中,由余弦定理 ( http: / / www.21cnjy.com )得SB2=SA2+AB2-2SA·AB·cos∠SAB=3002+(30t)2-2×300×30tcos60°=900t2-9000t+90000.
若S岛受到台风影响,则应满足条件SB≤270,即SB2≤2702,化简整理得t2-10t+19≤0,解得5-≤t≤5+.所以从现在起,经过(5-)hS岛开始受到台风的影响,(5+)h后影响结束,持续时间为(5+)-(5-)=2(h).
答:S岛将受到台风的影响,从现在起经过(5-)h,台风开始影响S岛,且持续时间为2h.
[题后反思] 此题为探索性命题,可以 ( http: / / www.21cnjy.com )假设命题成立去寻求解存在的条件,也可假设命题不成立去寻求解存在的条件.本题求解过程采用了第一种思路(SB≤270是否有解最终转化为关于t的一元二次不等式是否有解,与一元二次不等式解法相联系).
变式 海中有一小岛B,周围3.8n m ( http: / / www.21cnjy.com )ile内有暗礁,军舰由西向东航行到A处,望见岛B在北偏东75°的方向上;军舰又航行了8n mile到达C处,望见岛B在北偏东60°的方向上.若此军舰不改变航向而继续前进,有无触礁危险
( http: / / www.21cnjy.com )
(变式)
[处理意见] 军舰继续向东航行,有无触礁 ( http: / / www.21cnjy.com )的可能取决于B到直线AC的距离是否大于3.8n mile.于是我们只要先算出BC(或AB)的大小,再算出B到直线AC的距离,将它与3.8n mile比较即可得到答案.
[规范板书] 解 在△ABC中,AC=8,∠A=15°,∠ACB=150°,∴ ∠B=15°,从而BC=AC=8.∴ B到直线AC的距离为BC·sin30°=8×=4>3.8.因此,军舰不改变航向而继续航行,没有触礁的危险.
*【例3】 如图,已知扇形AOB的圆心 ( http: / / www.21cnjy.com )角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.[4]
( http: / / www.21cnjy.com )
(例3)
[处理建议] (1) 先帮助学生分析思路,然 ( http: / / www.21cnjy.com )后让学生解决;(2) △POC的面积会随θ的变化而变化,所以要用θ表示△POC的面积,因此首先要用θ表示OC.
[规范板书] 解 ∵ CP∥OB,∴ ∠OCP=120°,∴ ∠CPO=60°-θ.在△POC中,由正弦定理得OC===sin(60°-θ).
因此,△POC的面积为S(θ)=OP·OC·sinθ=sin(60°-θ)sinθ=sin(2θ+30°)-.
∵ 0°<θ<60°,∴ 当θ=30°时,S(θ)取得最大值为.
[题后反思] 此题是通过解三角 ( http: / / www.21cnjy.com )形来建立函数关系,然后利用三角函数的性质来求最值,这种通过建立函数模型来求最值是高考中常考的题型,提醒学生注意.
变式 如图,已知半圆的直径AB=2 ( http: / / www.21cnjy.com ),点C在AB的延长线上,BC=1,P为半圆上的一个动点,以PC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 设∠POB ( http: / / www.21cnjy.com )=θ,四边形OPDC的面积为y.在△POC中,由余弦定理得PC2=OP2+OC2-2·OP·OC·cos∠POC=5-4cosθ.
∴ y=S△POC+S△PCD=×2×1×sinθ+(5-4cosθ)=2sin+.
∵ 0≤θ≤π,∴ -≤θ-≤π,∴ 当θ-=,即θ=时,ymax=2+.∴ 四边形OPDC面积的最大值为2+.
二、 课堂练习
1. 在塔底所在水平面上的某点测得塔顶的仰角为θ,由此点向塔沿直线行走30m,测得塔顶的仰角为2θ,再向塔继续前进10m,又测得塔顶的仰角为4θ,则塔高是15m.
2. 某人沿正东方向走xkm后,向右转150°,然后朝新的方向走3km,结果他离出发点恰好 km,则x=或2.
提示 由题意可得cos30°=,化简得x2-3x+6=0,解得x=或x=2.
3. 如图,为了测量隧道AB的长度,给定下列四组数据,则测量应当选用数据③ .(填序号)
① α,a,b; ② α,β,a; ③ a,b,γ; ④ α,β,γ.
( http: / / www.21cnjy.com )
(第3题)
三、 课堂小结
1. 通过本节课的学习,我们知道正弦定理、 ( http: / / www.21cnjy.com )余弦定理有着非常广泛的应用.如果我们抽去每个应用题中与生产生活实际所联系的外壳,就暴露出解三角形问题的本质,这就需要我们在解决实际问题的过程中,不断提高分析问题和解决问题的能力,以及将实际问题转化为抽象的数学问题的能力.
2. 理解各种应用问题中的有关名词、术语,如坡度、俯角、仰角、方向角、方位角等.
3. 注意不等式、函数等代数知识的引入与应用.
第7课时 本章复习(1)
教学过程
一、 知识梳理
1. 正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 ===2R. a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
变形形式 a=2RsinA,b=2RsinB,c=2RsinC;a∶b∶c=sinA∶sinB∶sinC. cosA=,cosB=,cosC=.
作用 1. 已知两角和任一边,求另一角和其他两边;2. 已知两边和其中一边的对角,求另一边和其他两角. 1. 已知三边,求三个角;2. 已知两边和它们的夹角,求第三边和其他两个角.
2. 在△ABC中,已知a,b和A时,角B解的情况如下表:
A为锐角 A为钝角或直角
图形 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) (a>b情形的图形)
满足条件 ab a≤b
角B解的情况 无解 一解 两解 一解 一解 无解
3. 三角形中一些常用的结论:
(1) S△ABC=acsinB=bcsinA=absinC==r(a+b+c).(其中R,r分别为△ABC的外接圆和内切圆的半径)
(2) A>B a>b sinA>sinB.
二、 数学运用
正弦定理、余弦定理的应用包括两大方面:一是 ( http: / / www.21cnjy.com )数学内部的应用;二是实际应用.那么,正弦定理、余弦定理能解决数学内部哪些方面的问题呢 下面我们来看一看在三角形中的运用.
(一) 求解三角形中的基本元素
【例1】 在△ABC中,已知a=2, c=+, B=45°, 求b及A[1].
(见学生用书课堂本P13)
[处理建议] 引导学生审题,根据条件,已知a ( http: / / www.21cnjy.com ), c及其夹角B,自然想到先用余弦定理求出b;对于角A,可以利用余弦定理求得,也可以利用正弦定理求得.
[规范板书] ∵ b2=a2+c2-2accosB
=(2)2+(+)2-2×2×(+)×cos45°
=12+(+)2-4×(+1)
=8,
∴ b=2.
求A可以利用余弦定理,也可以利用正弦定理:
解法一 ∵ cosA=
==, 又∵A∈(0°, 180°), ∴ A=60°.
解法二 ∵ sinA=sinB=×sin45°=, 又∵ +>2.2+1.4=3.6, 2<2×1.8=3. 6, ∴ a[题后反思] 熟悉掌握正弦定理、余弦定理的应用,并加强运算能力的培养.
变式 已知某三角形的三边的长是三个连续的整数,最大角是最小角的2倍,求此三角形的最小边的长.
[处理建议] 设最小边的长为a ( http: / / www.21cnjy.com ),则另两边的长分别为a+1, a+2,三边长中只有一个未知量;设最小角为α,则最大角为2α,另一角为π-3α,三个角中也只有一个未知量,因此,只要建立两个方程就可求解.
[规范板书] 解 设最小边的长为a,最小角为α, 由正弦定理知=,得cosα=; 由余弦定理知cosα==, 解得a=4,所以最小边的长是4.
(二) 判断三角形的形状
【例2】 在△ABC中,若=,试判断△ABC的形状.[2] (见学生用书课堂本P13)
[处理建议] 三角形形状的判断方法是首先边化角或角化边,再整理化简即可判断.
[规范板书] 解法一 = = = sinAcosA=sinBcosB sin2A=sin2B 2A=2B或2A+2B=180°,即有A=B或A+B=90°.从而有A=B或C=90°,所以△ABC为等腰三角形或直角三角形.
解法二 = = = = acosA=bcosB a·=b· a2(b2+c2-a2)=b2(c2+a2-b2) (a2-b2)(a2+b2-c2)=0,即有a2=b2或a2+b2=c2,所以△ABC为等腰三角形或直角三角形.
[题后反思] (1) 依据已知条件中的边角关 ( http: / / www.21cnjy.com )系判断三角形的形状时,主要有如下两种方法:① 利用正(余)弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;② 利用正(余)弦定理把已知条件转化为三角形内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
(2) 注意在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
变式 在△ABC中,已知角A,B均为锐角,且cosA>sinB,试判断△ABC的形状.
[规范板书] 解 因为角A,B均为锐角,所以-A,B都是锐角.因为cosA>sinB,所以cosA=sin>sinB,则-A>B,即A+B<,所以C>,所以△ABC为钝角三角形.
(三) 三角形中的证明问题
【例3】 已知△ABC,证明:-=-.[3] (见学生用书课堂本P14)
[处理建议] 三角形中同时 ( http: / / www.21cnjy.com )含有边和角的等式的证明,通常要用正(余)弦定理进行边角归一,一是归为边的代数恒等式的证明,二是归为角的三角恒等式的证明.
[规范板书] 证明 左边=-=-=-=-=右边.故原命题得证.
变式 已知△ABC,证明:(a2-b2-c2)tanA+(a2-b2+c2)tanB=0.
[规范板书] 证明 左边=(a2-b2-c2)+(a2-b2+c2)=(a2-b2-c2)··+(a2-b2+c2)··=·(a2-b2-c2)·+·(a2-b2+c2)·=-+=0=右边.故原命题得证.
[题后反思] (1) 例3 ( http: / / www.21cnjy.com )的证明过程中用到了余弦二倍角公式,而此公式有三种形式(cos2A=cos2A-sin2A,cos2A=2cos2A-1,cos2A=1-2sin2A),由于考虑到等式右端为边的关系,故选用第三种形式,在转化为边的关系时较为简便.(2) 在变式题证明时应注意两点:一是切化弦的思路,二是结合正、余弦定理将角的关系转化为边的关系.
(四) 三角形中的求值问题
【例4】 在△ABC中,已知c=2,C=.
(1) 若△ABC的面积等于,求a,b;
(2) 若sinC+sin(B-A)=2sin2A,求△ABC的面积.[4] (见学生用书课堂本P14)
[处理建议] 主要是利用正、余弦定理,并结合三角形的面积公式来解题.
[规范板书] 解 (1) 由题意得a2+b2-ab=4,absinC=,所以ab=4,联立方程组解得
(2) 由题意得sin(B+A)+s ( http: / / www.21cnjy.com )in(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,即cosA(sinB-2sinA)=0.
当cosA=0时,A=,B=,a=,b=;
当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a,联立方程组解得
所以△ABC的面积S=absinC=.
[题后反思] (1) 对于三角形中的求值 ( http: / / www.21cnjy.com )问题,主要是利用正、余弦定理,并结合三角形的面积公式来解题;除此之外,更要善于利用方程思想来解题.(2) 可将第二小题作为变式让学生练习,让他们体会方程思想的应用.
(五) 正、余弦定理在几何中的应用
*【例5】 如图,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°,求BD的长.[5]
(例5)
[处理建议] 帮助学生分析思路:① ( http: / / www.21cnjy.com ) 由于AB=5,∠ADB=45°,因此要求BD,可在△ABD中,通过正弦定理求解,关键是确定∠BAD的正弦值;② 在△ABC中,AB=5,AC=9,∠BCA=30°,因此可利用正弦定理求出sin∠ABC,再依据∠ABC与∠BAD互补,确定sin∠BAD即可.
[规范板书] 解 在△ABC中,由正弦定理得sin∠ABC===.
∵ AD∥BC,∴ ∠BAD=180°-∠ABC,∴ sin∠BAD=sin∠ABC=.
在△ABD中,由正弦定理得BD===.
[题后反思] 正、余弦定理在几何中 ( http: / / www.21cnjy.com )的应用:① 首先根据已知量和未知量确定未知量所在的三角形;② 其次确定与未知量相关联的量;③ 最后把要求解的问题转化到由已知条件可直接求解的量上来.
( http: / / www.21cnjy.com )
(变式)
变式 如图,我炮兵阵地位于A ( http: / / www.21cnjy.com )处,两观察所分别设于B,D处,已知△ABD是边长等于a的正三角形,当目标出现于C处时,测得∠BDC=45°,∠CBD=75°,求炮击目标的距离AC.
[规范板书] 解 在△BCD中,由正弦定理得=,∴ BC=a.在△ABC中,由余弦定理得AC2=+a2-2×a·a·cos135°=a2,∴ AC=a.
答:炮击目标的距离AC为a.
三、 课堂练习
1. 在△ABC中,若A=60°,b=1,S△ABC=,则a=.
提示 S△ABC= bcsinA=×1·csin60°=c=,∴ c=4,从而a2=b2+c2-2bccosA=1+16-4=13,∴ a=.
2. 若△ABC的三个内角满足sinA∶sinB∶sinC=5∶11∶13,则△ABC的形状为钝角三角形.
提示 由正弦定理可得a∶b∶c=5∶11∶13.设a=5t,b=11t,c=13t,由余弦定理得cosC===-<0,所以C为钝角,故△ABC为钝角三角形.
3. 在△ABC中,已知=.
(1) 求的值;
(2) 若cosB=,b=2,求△ABC的面积S.
解 (1) =可化为=,即cosAsinB-2cosCsinB=2sinCcosB-sinAcosB,则cosAsinB+sinAcosB=2sinCcosB+2cosCsinB,所以sin(A+B)=2sin(C+B).而A+B+C=π,则sinC=2sinA,即=2.(也可以尝试用余弦定理来处理)
(2) 由(1)得c=2a,由余弦定理得4=c2+a2-2accosB=4a2+a2-a2=4a2,所以a=1,c=2.S=acsinB=×1×2×=.
四、 课堂小结
掌握利用正、余弦定理解决三角形内部问题的常见题型的处理方法和技巧.
第8课时 本章复习(2)
教学过程
一、 知识梳理
实际应用问题的处理方法和步骤归纳:
(1) 一般步骤:
① 分析:理解题意,分清已知与未知,画出示意图;
② 建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解三角形的数学模型;
③ 求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
④ 检验:检验上述所求的解是否具有实际意义,从而得出实际问题的解.
(2) 实际应用问题常有以下几种情形:
① 实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解;
② 实际问题经抽象概括后,已知量与未知量涉及两个三角形或多个三角形,这时需按顺序逐步在几个三角形中求出问题的解;
③ 实际问题经抽象概括后,涉及的三角形只有一个,但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.
二、 数学运用
正弦定理、余弦定理的应用包括两大 ( http: / / www.21cnjy.com )方面:一是数学内部的应用;二是实际应用.那么,正弦定理、余弦定理能解决实际应用中哪些方面的问题 下面我们来看一看在实际应用问题中的运用.
(一) 与距离有关的问题
【例1】 如图,A,B,C,D都在同 ( http: / / www.21cnjy.com )一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.在水面A处的船上测得B,D两点的仰角分别为75°和30°,在水面C处的船上测得B,D两点的仰角均为60°,AC=0.1km.
( http: / / www.21cnjy.com )
(例1)
(1) 求证:AB=BD.
(2) 求BD的长.[1] (见学生用书课堂本P15)
[处理建议] 思路解析:(1) 由已 ( http: / / www.21cnjy.com )知角度不难求得∠BCD,且易得AC=DC关系,利用三角形全等可得AB=BD;(2) 求BD只需将其转化在某个三角形中利用已知条件即可求.
[规范板书] 证明 (1) 在△A ( http: / / www.21cnjy.com )CD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,∴ CD=AC.又∠BCD=180°-60°-60°=60°,∴ ∠BCD=∠BCA,∴ △ACB≌△DCB.∴ BD=BA.
(2) 在△ABC中,由正弦定理得AB===,∴ BD=AB=(km).
[题后反思] (1) 要让学生熟练掌握正、余弦定理的应用;(2) 注意平面几何知识在求解过程中的应用.
变式 如图,公路MN和PQ在P处交汇 ( http: / / www.21cnjy.com ),且∠QPN=30°,在A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响 请说明理由;如果学校受到影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少
(变式)
[规范板书] 解 作AB⊥MN,垂足为B.在Rt△ABP中,∵ ∠ABP=90°,∠APB=30°,∴ AB=PA=80(m).∵ 点A到直线MN的距离小于100m,所以这所中学会受到噪声的影响.
如图,若以A为圆心、100m长为半径画圆,那么☉A和直线MN有两个交点,设交点分别为C,D,连结AC和AD,则AC=AD=100m.根据勾股定理和垂径定理得CD=2CB=2=120(m),∴ 学校受到噪声影响的时间为×3600=24(s).
(二) 与高度有关的问题
【例2】 某人在山顶观察地面上相距 ( http: / / www.21cnjy.com )2500m的A,B两个目标,测得A在南偏西57°的方向上,俯角为30°,同时测得B在南偏东78°的方向上,俯角是45°,求山高.(设A,B与山底在同一平面上,计算结果精确到0.1m)[2] (见学生用书课堂本P15)
[处理建议] 让学生分析 ( http: / / www.21cnjy.com )思路:(1) 在Rt△APQ和Rt△BPQ中,用高表示AQ,BQ;(2) 在斜△ABQ中,利用余弦定理建立方程,解出高.
[规范板书] 解 画出示意图(如图).
( http: / / www.21cnjy.com )
(1)
( http: / / www.21cnjy.com )
(2)
(例2)
设山高PQ=h,则在Rt△APQ和Rt△BPQ(如图(1))中,AQ==h,BQ==h.
在斜△ABQ(如图(2))中,∠AQB=57°+78°=135°,所以由余弦定理得AB2=AQ2+BQ2-2·AQ·BQ·cos∠AQB,即25002=+h2-2·h·h·cos135°,解得h=≈984.4(m).
所以山高约984.4m.
[题后反思] (1) 在测 ( http: / / www.21cnjy.com )量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内视线与水平线的夹角;(2) 准确理解题意,分清已知与所求,画出示意图;(3) 运用正、余弦定理,有序地解相关的三角形,逐步求解问题的答案,注意方程思想的运用.
变式 如图,测量河对岸的塔高AB ( http: / / www.21cnjy.com )时,可以选与塔底B在同一水平面内的两个观测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C处测得塔顶A的仰角为30°,求塔高AB.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 在△BCD中,∠CBD=180°-(75°+60°)=45°,由正弦定理得BC===s.在Rt△ABC中,AB=BC·tan30°=s.所以塔高AB为s.
(三) 与角度有关的问题
【例3】 在海岸A处,发现北偏西75°的方向、距离A处2n mile的B处有一艘走私船,若在A处北偏东45°的方向、距离A处(-1)n mile的C处的缉私船奉命以10n mile/h的速度追截走私船,此时,走私船正以10n mile/h的速度从B处沿北偏西30°的方向逃窜,问:缉私船沿什么方向才能最快追上走私船 所需时间为多少 [3] (见学生用书课堂本P16)
[处理建议] 思路解析:本例考查了 ( http: / / www.21cnjy.com )正弦定理、余弦定理的建模应用.如图所示,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求∠BCD.
[规范板书] 解 设xh后,它们在D处相遇,则CD=10xn mile,BD=10xn mile,∠CBD=120°.
( http: / / www.21cnjy.com )
(例3)
在△ABC中,AB=2,AC=-1,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=22+-2×2×(-1)×cos120°=6,∴ BC=.
而sin∠ACB===,∴ ∠ACB=45°,∴ BC与正北方向垂直.
在△BCD中,∠CBD=90°+30°=120°,由余弦定理得CD2=BC2+BD2-2BC·BD·cos∠CBD,即=+(10x)2-2××10x·cos120°,整理得200x2-10x-6=0,解得x=或x=-(舍去).
因此,在△BCD中,BD=,CD=3,∠CBD=120°.由正弦定理得sin∠BCD===,∴ ∠BCD=30°.
∴ 缉私船沿北偏西60°的方向才能最快追上走私船,所需时间为h.
[题后反思] (1) 测量角度,首先 ( http: / / www.21cnjy.com )应明确方位角、方向角等含义;(2) 在解应用题时,应先分析题意,分清已知与所求,再根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题中要注意体会正、余弦定理“联袂”使用的优点.
变式 如图,已知海中一小岛A周围3 ( http: / / www.21cnjy.com )8n mile内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°的方向上,船航行30n mile后,在C处测得小岛A在船的南偏东45°的方向上,如果此船不改变航向,继续往南航行,有无触礁的危险
( http: / / www.21cnjy.com )
(变式)
[处理建议] 船继续向南航行,有无触礁 ( http: / / www.21cnjy.com )的可能取决于A到直线BC的距离是否大于38n mile.于是我们只要先算出AC(或AB)的大小,再算出A到直线BC的距离,将它与38n mile比较即可得到答案.
[规范板书] 解 在△ABC中,BC=30,∠B=30°,∠ACB=135°,∴ ∠A=15°.由正弦定理得=,即=,∴ AC==15(+).
∴ A到直线BC的距离为AC·sin45°=15(+1)≈40.98(n mile),它大于38n mile,因此船不改变航向,继续向南航行,没有触礁的危险.
四、 课堂练习
1. 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,则AB边的长为5.
(第1题)
2. 已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若23cos2A+cos2A=0,a=7,c=6,则b=5.
3. 某人在C点测得某塔在南偏 ( http: / / www.21cnjy.com )西80°的方向上,塔顶仰角为45°,此人沿南偏东40°的方向前进10m到达D点,测得塔顶A的仰角为30°,求塔高.
解 如图,设塔高为h,在Rt△ACO中,∵ ∠ACO=45°,则OC=OA=h.
在Rt△ADO中,∵ ∠ADO=30°,则OD=h.
在△OCD中,∠OCD=80°+40°=120°,CD=10,由余弦定理得OD2=OC2+CD2-2·OC·CD·
cos∠OCD,即(h)2=h2+102-2h×10×cos120°,整理得h2-5h-50=0,解得h=10或h=-5(舍去).
答:塔高为10m.
( http: / / www.21cnjy.com )
(第3题)
五、 课堂小结
有关斜三角形的实际问题,其解题的一般步骤是:
(1) 准确理解题意,分清已知与所求,尤其要理解应用题中的有关名词和术语;
(2) 画出示意图,并将已知条件在图形中标出;
(3) 分析与所研究问题有关的一个或几个三角形,合理运用正弦定理和余弦定理求解.
第1课时 正弦定理(1)
教学过程
一、 问题情境
1. 对于“即时体验”中的第2题:“在△ABC中,若C=75°,A=60°,b=,则这个三角形能确定吗 B,a,c能求出来吗 ”这个三角形虽然可以确定,但根据我们目前所掌握的知识还不能够求出a,c,这说明了什么呢 这只能说明我们对三角形中的边角之间的关系还缺乏足够的了解,还没有发现它们之间所隐含的规律.
2. 三角形中的边角之间究竟隐含着什么样的规律呢 还是让我们从特殊情况来考察:在Rt△ABC中,C=90°,试判定,与之间的大小关系.
二、 数学建构
问题1 对任意三角形,==也成立吗
用几何画板演示,如果不具备条件的话,也可以通过纸笔或计算器来计算任意三角形中三边长与其对角的正弦值之比,让学生通过验证感受到:对任意三角形,都有==
问题2 验证能代替证明吗
(验证不能代替证明,验证只是表明个别情形或特殊情形成立,还不能说明一般情形或任意情形都成立)
问题3 如何证明对任意三角形都有==成立呢
(根据教材P5中的途径提示,组织学生进行讨论,最好能由学生给出证明思路)
对于==这一关系的证明,我们一起来看下面的证法.
( http: / / www.21cnjy.com )
(图1)
证法一:在△ABC中,有=+.不妨设∠C为最大角,过点A作AD⊥BC于D(如图1),于是·=(+)·=·+·,即0=||||cos(90°+B)+||||cosα,其中,当∠C为锐角或直角时,α=90°-C;当∠C为钝角时,α=C-90°.故可得csinB-bsinC=0,即=.同理可得=,所以==.
上述等式表明,三角形的各边和它所对角的正弦之比相等.这样,我们得到正弦定理:==.
问题4 对于正弦定理:==,你还能尝试用其他方法证明吗
( http: / / www.21cnjy.com )
(图2)
( http: / / www.21cnjy.com )
(图3)
证法二[2]:设☉O是△ABC的外接圆,直径BD=2R.
(1) 当A为锐角时,如图2,连结CD,则∠BCD=90°,a=2RsinD.又∠D=∠A,所以a=2RsinA.
(2) 当A为钝角时,如图3,连结CD, ( http: / / www.21cnjy.com )则∠BCD=90°,a=2RsinD.又∠D+∠A=180°,可得sinD=sin(180°-A)=sinA,所以a=2RsinA.
(3) 当A为直角时,a=2R,显然有a=2RsinA.
综上所述,所以不论A是锐角、钝角或直角,总有a=2RsinA.
同理可证b=2RsinB,c=2RsinC.
所以===2R.
这就是说,对于任意的三角形,上述关系式均成立,即三角形的各边和它所对角的正弦之比相等,因此,我们得到正弦定理:===2R.
正弦定理的变形:a=2RsinA,b=2R ( http: / / www.21cnjy.com )sinB,c=2RsinC(2R是△ABC外接圆的直径);a∶b∶c=sinA∶sinB∶sinC.
问题5 在课前预习时,“即时体验”中的第2题你解决了吗
三、 数学运用
【例1】 (教材P7例1)在△ABC中,A=30°,C=100°,a=10,求b,c.(精确到0.01)[3]
(见学生用书课堂本P1)
( http: / / www.21cnjy.com )
(例1)
[处理建议] (1) 先让学生自己动手作图 ( http: / / www.21cnjy.com ),看看此三角形是否确定,然后再考虑如何求B,b,c.(2) 理清解题思路:如图,直接应用正弦定理可求出边c;若求边b,则需通过三角形内角和为180°先求出角B,再利用正弦定理求出边b.
[规范板书] 解 B=180°-(A+C)=180°-(30°+100°)=50°.
因为==,所以b==≈15.32,c==≈19.70.
因此,b,c分别为15.32和19.70.
[题后反思] (1) 此类 ( http: / / www.21cnjy.com )问题结果为唯一解,学生较易掌握;如果已知两角和两角所夹的边去求其他边角,也是先利用内角和为180°求出第三角,再利用正弦定理求出其他边.(2) 因此,对“已知两角与任一边,求其他两边和一角”的问题都能够用正弦定理彻底解决,且解唯一.
变式 在△ABC中,已知A=60°,B=45°,c=3,求C,a,b.
[规范板书] 解 C=180°-(A+B)=180°-(60°+45°)=75°.因为==,所以a===,b===3-3.因此,C,a,b分别为75°,和3-3.
【例2】 根据下列条件解三角形:
(1) a=14,b=7,B=60°;
(2) c=,b=,B=45°.[4]
(见学生用书课堂本P2)
[处理建议] (1) 解三角形是指由六 ( http: / / www.21cnjy.com )个元素中的三个元素(至少有一个是边),求其余三个未知元素的过程;(2) 对于本题,先让学生讨论,尝试解答;然后教师在学生中交流,了解学生的思考过程,投影学生的求解过程,并纠正出现的错误.
[规范板书] 解 (1) ∵ a
当C1=60°时,A1=180°-(C1+B)=180°-(60°+45°)=75°,a1===1+;
当C2=120°时,A2=180°-(C2+B)=180°-(120°+45°)=15°,a2===1-.
[题后反思] (1) 同样是已知两边和一边的对角,但可能出现不同的结果,应向学生强调注意解题的灵活性.
(2) 对于第(1)题,如果没有考 ( http: / / www.21cnjy.com )虑到角A所受到的限制而求出角A的两个解,进而求出边a有两解,那么也可利用三角形两边之和大于第三边,两边之差小于第三边这一性质进行验证,进而排除不符题意的解.
(3) 思考:对于第(1)、(2)题,能否通过作图来分析为什么解的个数不一样 为什么第(2)题产生多解 (引导学生通过作出三角形来思考)
“已知两边和其中一边的对角,求另一边的对角”这类问题情形复杂,但若通过作图来考虑,情形就一目了然了.
① A为锐角:
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
注意:当a
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
变式 在△ABC中,已知c=5,A=45°,试判断当a分别取10,5,,时,角C的解的个数.
[规范板书] 解 (1) 当a=10时,有a>c,故角C有一解;
(2) 当a=5时,∵ csinA=5sin45°=5,∴ a=csinA,故角C有一解;
(3) 当a=时,有c>a>csinA=5sin45°=5,故角C有两解;
(4) 当a=时,有a
[处理建议] 先让学生分析得出条件与三角形的角有关,结论与三角形的角的正弦值有关.但是如何实现条件与结论的转化呢 自然联想到正弦定理.
[规范板书] 证明 因为a=2Rs ( http: / / www.21cnjy.com )inA,b=2RsinB,所以A>B a>b 2RsinA>2RsinB sinA>sinB,即A>B sinA>sinB.
[题后反思] (1) 不能利用正弦函数的单调 ( http: / / www.21cnjy.com )性进行证明,因为正弦函数在(0,π)内不具有单调性;(2) 在△ABC中,有A>B a>b sinA>sinB cosA
1. 在△ABC中,
(1) 已知A=30°,B=120°,b=8,求a;
(2) 已知A=45°,B=60°,c=,求b.[5]
解 (1) ∵ =,∴ a===.
(2) ∵ C=180°-(A+B)=180°-(45°+60°)=75°,=,∴ b===(-).
2. 根据下列条件解三角形:
(1) a=2,b=2,B=60°;
(2) a=,b=,B=45°.[6]
解 (1) ∵ =,∴ sinA===,∴ A1=30°,A2=150°.
当A1=30°时,C1=180°-(A1+B)=180°-(30°+60°)=90°,∴ c1===4;
当A2=150°时,A2+B=150°+60°>180°,故A2=150°应舍去(或者由a
(2) ∵ =,∴ sinA===,∴ A1=60°,A2=120°.
当A1=60°时,C1=180°-(A1+B)=180°-(60°+45°)=75°,∴ c1===;
当A2=120°时,C2=180°-(A2+B)=180°-(120°+45°)=15°,∴ c2===.
∴ A=60°,C=75°,c=,或A=120°,C=15°,c=.
五、 课堂小结
1. 正弦定理及其变形形式:
(1) ===2R(2R是△ABC外接圆的直径);
(2) a=2RsinA,b=2RsinB,c=2RsinC,或a∶b∶c=sinA∶sinB∶sinC.
2. 利用正弦定理,可以解决以下两类有关三角形问题:
(1) 已知两角和任一边,求其他两边和一角;(这类问题由于两角已知,故第三角确定,三角形确定,解唯一,相对容易)
(2) 已知两边和其中一边的对角,求另一边的对角.(此类问题相对复杂些,要防止多解和少解的发生)
第2课时 正弦定理(2)
教学过程
一、 问题情境
问题1 你能举出在现实生活中哪些方面有可能会运用到解三角形的知识
问题2 你能举出在数学本身内部哪些方面有可能会运用到解三角形的知识
二、 数学运用
【例1】 (根据教材P9例 ( http: / / www.21cnjy.com )3改编)如图,某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为15°的斜坡前进1000m后到达D处,又测得山顶B的仰角为75°,求山的高度BC.[2](见学生用书课堂本P3)
( http: / / www.21cnjy.com )
(例1)
[处理建议] (1) 让学生重新动手作图,从中理顺关系;(2) 要求BC,只要求出AB即可,因此考虑解△ABD.
[规范板书] 解 过点D作DE∥AC交BC于E,因为∠DAC=15°,所以∠ADE=165°,于是∠ADB=360°-165°-75°=120°.又∠BAD=45°-15°=30°,所以∠ABD=30°.在△ABD中,由正弦定理,得AB===1000(m).在Rt△ABC中,BC=AB·sin45°=1000×=500(m).
答:山的高度为500m.
[题后反思] (1) 此 ( http: / / www.21cnjy.com )题是正弦定理在高度测量问题中的应用,教学时应引导学生寻找和分析条件与结论所涉及的三角形中的边角关系;(2) 复杂的应用题,涉及的往往不止一个三角形,要在不同的三角形中求出需要的边和角,再在一个三角形中解决主要问题,这就需要我们处理问题要有先后次序、条理清晰、目标明确.
变式 一货轮航行到M处,测得灯塔S在货 ( http: / / www.21cnjy.com )轮的北偏东15°相距20n mile处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔S在货轮的北偏东45°方向上,求货轮的航行速度.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 设货轮的航行速度为vnmile/h,如图,在△MNS中,MS=20n mile,MN=v,∠NMS=30°+15°=45°,∠MNS=180°-30°-45°=105°,从而∠MSN=30°.由正弦定理得=,即=,所以v=20(-)(nmile/h).
【例2】 已知△ABC,证明:a=bcosC+ccosB(射影定理).[3] (见学生用书课堂本P4)
[处理建议] 让学生回顾教材P56中正弦定理的证法一,进而使他们从中受到启发.
[规范板书] 证明 由正弦定理得a=2 ( http: / / www.21cnjy.com )RsinA,b=2RsinB,c=2RsinC,所以bcosC+ccosB=2RsinBcosC+2RsinCcosB=2Rsin(B+C)=2Rsin(180°-A)=2RsinA=a,所以a=bcosC+ccosB.
[题后反思] (1) 三角形中的三 ( http: / / www.21cnjy.com )角恒等式的证明,通常采用的方法是边角归一,即转化为边,或转化为角的单一的形式来证明;(2) 实现边角归一的工具是正(余)弦定理;(3) 要在解题的实践中不断积累这类题的解题方法.
变式 (教材P10例5) 在△ABC中,AD是∠BAC的平分线(如图),证明:=.(内角平分线定理)
( http: / / www.21cnjy.com )
(变式)
[规范板书] 证明 设∠BAD=α,∠BDA=β,则∠CAD=α,∠CDA=180°-β.在△ABD和△ACD中分别运用正弦定理,得=,==,所以=,即=.
*【例3】 在△ABC中,已知acosA=bcosB,试判断△ABC的形状.[4]
[处理建议] (1) 让学生回忆:特殊三角形有哪些 它们又是如何定义的 (2) 启发学生从角或边考虑,寻求解题途径.
[规范板书] 解 acosA=bcosB ( http: / / www.21cnjy.com ) 2RsinAcosA=2RsinBcosB Rsin2A=Rsin2B sin2A=sin2B 2A=2B或2A+2B=180°,即有A=B或A+B=90°,从而有A=B或C=90°.所以,此三角形为等腰三角形或直角三角形.
[题后反思] (1) 此题是关于三角 ( http: / / www.21cnjy.com )形的形状判断的问题,判断三角形的形状,通常是指等腰三角形、等边三角形、直角三角形或等腰直角三角形等特殊三角形;(2) 此类问题,主要是借助于正(余)弦定理,将三角形中边的关系与角的关系相互转化:一方面可以转化为边的关系来判断;另一方面可以转化为角的关系来判断.此题是转化为角来判断的,学过余弦定理后,此题也可以转化为边来判断;(3) 防止遗漏2A+2B=180°的发生.
变式 (教材P9例4)在△ABC中,已知==,试判断△ABC的形状.
[规范板书] 解 == == == tanA=tanB=tanC.又A,B,C∈(0,π),所以A=B=C,从而△ABC为正三角形.
三、 课堂练习
1. 海上有相距10n mile的A,B两个小岛,从A岛望B岛和C岛成60°角(即∠BAC=60°),从C岛望B岛和A岛成45°角(即∠ACB=45°),则B,C两岛之间的距离是5n mile.
提示 由正弦定理得BC===5(n mile).
2. 在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=1∶∶2.
提示 由A∶B∶C=1∶2∶3及A+B+C=180°,可求得A=30°,B=60°,C=90°.从而a∶b∶c=sinA∶sinB∶sinC=sin30°∶sin60°∶sin90°=1∶∶2.
3. 在△ABC中,已知b=2csinB,求角C.
解 由b=2csinB,得2RsinB=2×2RsinCsinB,即sinB(1-2sinC)=0.因为sinB≠0,所以sinC=.又C∈(0,π),因此C=或.
4. 在△ABC中,已知==,判断△ABC的形状.
解 由正弦定理得==,所以tanB=tanC=1.又B,C∈(0,π),所以B=C=,从而A=.因此,△ABC为等腰直角三角形.
四、 课堂小结
通过本节课的学习,了解到正弦定理的应用主要体现在以下几个方面:
(1) 求三角形中的基本元素;
(2) 三角形中恒等式的证明;
(3) 判断三角形的形状:
给出三角形中的三角关系式,判断三角形的形状,通常有两种方法:① 统一化为角,再判断;② 统一化为边,再判断.
此外,在三角形中,对于恒等式的证明和三角形形状的判断这两类问题,尤其要注意正弦定理的变形形式的使用.
第3课时 余弦定理(1)
教学过程
一、 问题情境
1. 在前面我们通过研究发现了正弦定 ( http: / / www.21cnjy.com )理,并运用正弦定理解决了三角形中的两类问题.当两边夹一角或三条边确定了,这个三角形就确定了,其余的边和角也就确定了,但我们无法用正弦定理求出其余的边和角,这说明了什么呢 这只能说明我们对三角形的探究还不够深入,三角形中的边角关系我们还没有完全掌握,接下来我们该怎么办呢
2. 在上节课中,我们通过等式=+的两边与(AD为△ABC中BC边上的高)作数量积,将向量等式转化为数量关系,进而推出了正弦定理.具体是如何操作的,你还有印象吗
二、 数学建构
问题1 还有其他途径将向量等式=+数量化吗
(,,这三个向量的模与三角形的边长有关,它们的夹角与三角形的角有关,引导学生分析出:两边平方)
·=(+)·(+)
=+2·+
=||2+2||||cos(π-A)+||2
=c2-2cbcosA+b2,
即a2=b2+c2-2bccosA.
同理可得b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
上述等式表明,三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.这样我们就得到余弦定理:
余弦定理(形式一):a2=b2+c2-2bccosA,
b2=c2+a2-2cacosB,
c2=a2+b2-2abcosC.
问题2 回顾正弦定理不同的证明方法,你还能尝试用其他方法证明余弦定理吗
(引导学生回顾通过建立平面直角坐标系,利用三角函数的定义证明正弦定理的方法,对照余弦定理的特点,产生如下证法)
证明:建立如图1所示的平面直角坐标系,则A(0,0),B(ccosA,csinA),C(b,0).
( http: / / www.21cnjy.com )
(图1)
所以a2=(ccosA-b)2+(csinA)2
=c2cos2A+c2sin2A-2bccosA+b2
=b2+c2-2bccosA.
同理可得b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
(此证明方法的优点在于不必对角A进行锐角、直角、钝角等分类讨论)
余弦定理也可以写成如下形式:
余弦定理(形式二):cosA=,cosB=,cosC=.
问题3 余弦定理a2=b2+c2-2bccosA这种形式能帮助我们解决正弦定理不能解决的什么问题
(引导学生分析等式左右两边的特 ( http: / / www.21cnjy.com )点:右边涉及两边及其夹角,而左边涉到夹角的对边.即已知两边和它们的夹角,利用这种形式的余弦定理可求出第三边,进而求出其他两个角)
问题4 余弦定理cosA=这种形式能帮助我们解决正弦定理不能解决的什么问题
(引导学生分析等式左右两边的特点:右边 ( http: / / www.21cnjy.com )涉及三边,而左边涉及一角.即已知三边,利用这种形式的余弦定理可求出三个角.这样,问题3、问题4对于正弦定理不能解决的两类遗留问题应用余弦定理就能彻底解决了)
三、 数学运用
在证明了余弦定理之后,我们来进一步学习余弦定理的应用.
利用余弦定理,可以解决以下两类有关三角形的问题:
(1) 已知三边,求三个角;(这类问题由于三边确定,故三角也确定,解唯一)
(2) 已知两边和它们的夹角,求第三边和其 ( http: / / www.21cnjy.com )他两个角.(这类问题第三边是确定的,因而其他两个角唯一,故解唯一;不会产生类似利用正弦定理解三角形时所产生的判断取舍等问题)
接下来,我们通过例题进一步体会与总结.
【例1】 (根据教材P14例1改编)在△ABC中,
(1) 已知b=8,c=3,A=60°,求a;
(2) 已知a=2,b=,c=+1,求A.[2]
(见学生用书课堂本P5)
[处理建议] (1) 第一小 ( http: / / www.21cnjy.com )题属于已知两边及夹角求边的类型,可通过余弦定理形式一求出第三边;第二小题属于已知三角形三边求角的类型,可以利用余弦定理形式二求出角;(2) 这两小题是余弦定理直接简单的应用,可以让学生板演,培养学生的计算能力.
[规范板书] 解 (1) 由a2=b2+c2-2bccosA,得
a2=82+32-2×8×3×cos60°=49,∴ a=7.
(2) 由cosA=,得
cosA==,∴ A=45°.
[题后反思] (1) 若将例1的要求改为解三角形,那么后继问题又该怎样解决呢
(2) 对于已知两边及夹角解三角形的类 ( http: / / www.21cnjy.com )型,可通过余弦定理形式一先求出第三边,在第三边求出后,其余两角求解有两种思路:一是利用余弦定理形式二根据三边求第二个角,第三个角用三角形内角和定理求出;二是利用正弦定理根据两边及一边对角求解(但若用正弦定理求解,需对两种结果进行判断取舍,而在0°180°内,余弦有唯一解,故用余弦定理较好).
(3) 在解三角形时,如果正弦定理与余弦定理均可选用,那么求边用两个定理均可,求角用余弦定理则可免去判断取舍的麻烦.
【例2】 (教材P14例3)证明:在△ABC中,当∠C为锐角时,a2+b2>c2;当∠C为钝角时,a2+b2
[处理建议] 条件是角,结论是边,而且还涉及三条边,自然会想到用余弦定理.
[规范板书] 证明 当∠C为锐角时,cosC>0,由余弦定理得cosC=>0,即a2+b2-c2>0,所以a2+b2>c2.
同理可证,当∠C为钝角时,a2+b2
变式 钝角△ABC的三边的长为连续的自然数,求三边的长.
[规范板书] 解 不妨设a=n,b=n+1,c=n+2(n∈N*),则角C为最大角且为钝角.
∴ cosC=<0,∴ a2+b2-c2<0,∴ a2+b2
*【例3】 在△ABC中,已知a=8,b=7,B=60°,求c及S△ABC.[4]
[处理建议] (1) 思路一:根据已知条件可以先由正弦定理求出角A,再结合三角形内角和定理求出角C,再利用正弦定理求出边c,而三角形面积由公式S△ABC=acsinB可以求出.(2) 思路二:若用余弦定理求c,表面上缺少角C,但可利用余弦定理b2=c2+a2-2cacosB建立关于c的方程,也能达到求c的目的.
[规范板书] 解法一 由正弦定理得=,∴ sinA=.∵ a>b,∴ A>B=60°,∴ A有两解,∴ A1≈81.8°,A2≈98.2°.∴ C1=38.2°,C2=21.8°.由=,得c1=5,c2=3.∴ S△ABC=ac1sinB=10或S△ABC=ac2sinB=6.
解法二 由余弦定理得72=c2+82-2×8·c·cos60°,整理得c2-8c+15=0,解得c1=5,c2=3.∴ S△ABC=ac1sinB=10或S△ABC=ac2sinB=6.
[题后反思] (1) 在解法一中,注意 ( http: / / www.21cnjy.com )利用正弦定理应有两种结果,避免遗漏;而解法二更有耐人寻味之处,体现出余弦定理作为公式而直接应用的另外用处,即可以用之建立方程,从而运用方程的观点去解决问题,故解法二应引起学生的注意.
(2) 通过上述例题,可要求学生总结余弦 ( http: / / www.21cnjy.com )定理在求解三角形时的适用范围(已知三边求任意角或已知两边及夹角解三角形),同时注意余弦定理在求角时的优势以及利用余弦定理建立方程的解法.
变式 在△ABC中,已知a=7,c=5,A=120°,求的值.
[规范板书] 解 由余弦定理得72=b2+52-2×5·b·cos120°,整理得b2+5b-24=0,解得b1=3,b2=-8(舍去).所以==.
四、 课堂练习
1. 在△ABC中,
(1) 若a=20,b=29,c=21,则B=90°;
(2) 若a=3,c=2,B=150°,则b=7.[5]
提示 (1) ∵ cosB===0,∴ B=90°.
(2) ∵ b2=c2+a2-2cacosB=22+(3)2-2×2×3×=49,∴ b=7.
2. 若三条线段的长分别为5,6,7,则用这三条线段构成的三角形中最大角的正弦值为.
提示 不妨设在构成的△ABC中,a=5,b=6,c=7,对应的角分别为A,B,C,则最大的角为C.∵ cosC===,∴ sinC=.
3. 在△ABC中,若a2=b2+c2+bc,则A=120°.
提示 ∵ cosA=
==-,∴ A=120°.
五、 课堂小结
通过本节课的学习,我们一起研究了余弦定理的证 ( http: / / www.21cnjy.com )明方法,同时又进一步了解了向量的工具性作用,并且明确了利用余弦定理可以解决以下两类有关三角形的问题:
(1) 已知三边,求三个角;(这类问题由于三边确定,所以三角也确定,故解唯一)
(2) 已知两边和它们的夹角,求第三 ( http: / / www.21cnjy.com )边和其他两个角.(这类问题第三边是确定的,因而其他两个角唯一,故解唯一;不会产生类似利用正弦定理解三角形时所产生的判断取舍等问题)
第4课时 余弦定理(2)
教学过程
一、 问题情境
1. 你能举出在现实生活中与解三角形有关,但又是正弦定理所解决不了的例子吗
2. 你能举出在数学本身内部哪些方面有可能会运用到余弦定理知识的例子吗
二、 数学运用
( http: / / www.21cnjy.com )
(例1)
【例1】 如图,甲船以30n mile/h的速度向正北方向航行,乙船按某固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船北偏西105°方向的B1处,此时两船相距20n mile;当甲船航行20min到达A2处时,乙船航行到甲船北偏西120°方向的B2处,此时两船相距10n mile.问:乙船每小时航行多少海里 [2]
(见学生用书课堂本P7)
[处理建议] (1) 让学生读懂题意,帮助学生正确构造三角形是关键;(2) 让学生自己结合题设条件、正弦定理或余弦定理求解.
[规范板书] 解 如图1,连结A1B2,由已知得A2B2=10,A1A2=30×=10,∴ A1A2=A2B2.又∠A1A2B2=180°-120°=60°,∴ △A1A2B2是等边三角形,∴ A1B2=A1A2=10.由已知得A1B1=20,∠B1A1B2=105°-60°=45°.
( http: / / www.21cnjy.com )
(图1)
在△A1B2B1中,由余弦定理得B1=A1+A1-2A1B1·A1B2·cos45°=202+(10)2-2×20×10×=200,∴ B1B2=10.因此,乙船的速度为×60=30(n mile/h).
答:乙船每小时航行30n mile.
变式 如图2,若连结A2B1,此题又如何求解呢
( http: / / www.21cnjy.com )
(图2)
[规范板书] 解 如图2,连结A2B1,由已知得A1B1=20,A1A2=30×=10,∠B1A1A2=105°.
在△A2A1B1中,由余弦定理得A2=A1+A1-2A1B1·A1A2·cos105°=(10)2+202-2×10×20×=100(4+2),∴ A2B1=10(1+).
由正弦定理得sin∠A1A2B1=·sin∠B1A1A2=·=,∴ ∠A1A2B1=45°,则∠B1A2B2=60°-45°=15°.
在△B1A2B2中,A2B2=10,由余弦定理得B1=A2+A2-2A2B1·A2B2·cos15°=[10(1+)]2+(10)2-2×10(1+)×10×=200,∴ B1B2=10.因此,乙船的速度为×60=30(n mile/h).
答:乙船每小时航行30n mile.
[题后反思] 变式的解法也是构造三角形的一种方法,但计算量大,通过比较,要让学生善于利用条件优化解题过程.
【例2】 在△ABC中,已知acosB=bcosA,试判断△ABC的形状.[3] (见学生用书课堂本P8)
[处理建议] 对于三角形形状的判断,可 ( http: / / www.21cnjy.com )以根据角的关系,也可以根据边的关系,所以在已知条件的运用上,可以考虑两种途径:① 将边转化为角;② 将角转化为边.让学生从这两个角度进行分析.
[规范板书] 解法一 (利用余弦定理化角为边)acosB=bcosA a·=b· c2+a2-b2=b2+c2-a2,∴ 2a2=2b2,即a=b.故此三角形是等腰三角形.
解法二 (利用正弦定理化边为角)acos ( http: / / www.21cnjy.com )B=bcosA 2RsinAcosB=2RsinBcosA,∴ sinAcosB-cosAsinB=0,∴ sin(A-B)=0(亦可变到tanA=tanB).∵ -π
变式 在△ABC中,已知2cosBsinA=sinC,试判断△ABC的形状.
[规范板书] 解法一 2cosBsinA=sinC 2cosBsinA=sin[π-(A+B)] 2cosBsinA=sin(A+B) 2cosBsinA=sinAcosB+cosAsinB cosBsinA=cosAsinB = tanA=tanB.
又A,B∈(0,π),所以A=B.因此,△ABC为等腰三角形.
解法二 由正、余弦定理得2cosBsinA=sinC 2··= c2+a2-b2=c2 a2=b2 a=b.因此,△ABC为等腰三角形.
【例3】 (根据教材P16例6改编)在 ABCD中,证明:AC2+BD2=2(AB2+AD2).[4]
( http: / / www.21cnjy.com )
(例3)
(见学生用书课堂本P8)
[处理建议] (1) 利用正(余)弦 ( http: / / www.21cnjy.com )定理的前提是必须在三角形中,在四边形中如何选择有用的三角形是关键;(2) 任何一个三角形都不可能包含四边,因此必须选择两个三角形,让学生按此思路,往下思考.
[规范板书] 证明 设∠ABC=α,∠ ( http: / / www.21cnjy.com )BCD=π-α.在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BC·cosα ①.在△BCD中,由余弦定理得BD2=CD2+BC2-2CD·BC·cos(π-α) ②.因为cos(π-α)=-cosα,CD=AB,BC=AD,将①②两式相加得AC2+BD2=2(AB2+AD2).
[题后反思] 几何证明的关键是把有关量放到三角形中,借助正(余)弦定理,建立它们的关系,从而达到证明的效果,其中构造三角形是关键.
( http: / / www.21cnjy.com )
(变式)
变式 (教材P16例6)如图,若AM是△ABC中BC边上的中线,求证:AM=.
[规范板书] 证明 设∠AMB=α,则∠AMC=180°-α.在△ABM中,由余弦定理,得AB2=AM2+BM2-2AM·BMcosα.在△ACM中,由余弦定理,得AC2=AM2+MC2-2AM·MCcos(180°-α).因为cos(180°-α)=-cosα,BM=MC=BC,所以AB2+AC2=2AM2+BC2,因此,AM=.
*【例4】 在△ABC中,求证:a2sin2B+b2sin2A=2absinC.[5]
[处理建议] 此题所证结论包 ( http: / / www.21cnjy.com )含△ABC的边角关系,证明时可以考虑两种途径:一是把角的关系通过正、余弦定理转化为边的关系;二是把边的关系转化为角的关系,一般是通过正弦定理.让一部分学生走“化为边”这一途径,让另一部分学生走“化为角”这一途径.
[规范板书] 证法一 (化 ( http: / / www.21cnjy.com )边为角)a2sin2B+b2sin2A=(2RsinA)22sinB·cosB+(2RsinB)22sinA·cosA=8R2sinA·sinB(sinAcosB+cosAsinB)=8R2sinAsinBsinC=2·2RsinA·2RsinB·sinC=2absinC.所以原式得证.
证法二 (化角为边)左边=a2·2sinBcosB+b2·2sinAcosA=a2··+b2··=(a2+c2-b2+b2+c2-a2)=·2c2==2ab·=2absinC=右边.所以原式得证.
[题后反思] (1) 由边向角转化,通常利 ( http: / / www.21cnjy.com )用正弦定理的变形形式(a=2RsinA,b=2RsinB,c=2RsinC),在转化为角的关系式后,要注意三角函数公式的运用,在此题证明过程中用到了正弦二倍角公式sin2A=2sinAcosA,正弦两角和公式sin(A+B)=sinAcosB+cosAsinB;由角向边转化,要结合正弦定理变形形式以及余弦定理形式二.
(2) 三角形中的有关证明问题,主要是围绕三角形的边和角的三角函数展开,从某种意义上来看,这类问题就是有了目标的含边和角的式子的化简问题.
变式 已知△ABC,请用余弦定理证明:a=bcosC+ccosB.
[规范板书] 证明 bcosC+ccosB=b·+c·===a,即有a=bcosC+ccosB.
四、 课堂练习
1. 在 ABCD中,已知B=120°,AB=6,BC=4,则AC=2,BD=2.
提示 由余弦定理得AC2=AB2+BC2-2·AB·BC·cosB=62+42-2×6×4×cos120°=76,∴ AC=2.由余弦定理得BD2=AD2+AB2-2·AD·AB·cosA=42+62-2×4×6×cos60°=28,∴ BD=2.
2. 在△ABC中,证明:b=ccosA+acosC.(请你尝试用两种不同方法证明)
证法一 ccosA+acosC=2RsinC ( http: / / www.21cnjy.com )cosA+2RsinAcosC=2Rsin(A+C)=2Rsin(π-B)=2RsinB=b,即b=ccosA+acosC.
证法二 ccosA+acosC=c·+a·==b,即证.
3. 在△ABC中,已知a,b是方程x2-2x+2=0的两个根,且2cos(A+B)=-1,求c.
解 ∵ 2cos(A+B)=-1,∴ cos(A+B)=-,而0
1. 我们熟悉了正、余弦定理在进行边角关系转换时的桥梁作用,并利用了正、余弦定理对三角恒等式进行证明以及对三角形形状进行判断.
2. 我们要体会正、余弦定理的边角转换功能,注意常见解题方法与解题技巧的总结,不断提高三角形问题的求解能力.
第5课时 正弦定理、余弦定理的应用(1)
教学过程
一、 问题情境
问题 复习前两节的例题、练习、习题,总结一下:正弦定理、余弦定理能解决实际中的哪些问题
(正弦定理、余弦定理体现了三角形中边角之间的 ( http: / / www.21cnjy.com )相互关系,在测量、航海、几何、物理学等方面都有非常广泛的应用.下面,我们将举例来说明解三角形在实际中的一些应用)
二、 数学建构
正弦定理:===2R;
a=2RsinA,b=2RsinB,c=2RsinC;
a∶b∶c=sinA∶sinB∶sinC.
余弦定理:a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC;
cosA=,cosB=,cosC=.
三、 数学运用
【例1】 如图,位于A处的信 ( http: / / www.21cnjy.com )息中心获悉:在其正东方向相距40n mile的B处有一艘渔船遇险,正在原地等待营救.信息中心立即把这一消息告知在其南偏西30°方向、相距20n mile的C处的乙船,现乙船朝北偏东θ的方向沿直线CB前往B处救援,求cosθ的值.[2] (见学生用书课堂本P9)
( http: / / www.21cnjy.com )
(例1)
[处理建议] 思路解析:本例考查 ( http: / / www.21cnjy.com )了正弦定理、余弦定理的建模应用.如图,确定θ,关键是确定∠ACB,于是问题转化为求△ABC中的∠ACB,应用问题就转化为解三角形问题.
[规范板书] 解 连接BC,在△ABC中,AB=40,AC=20,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=402+202+2×40×20×=2800,∴ BC=20.由正弦定理得sin∠ACB===.由∠BAC=120°,知∠ACB为锐角,则cos∠ACB=.由θ=∠ACB+30°,得cosθ=cos(∠ACB+30°)=cos∠ACBcos30°-sin∠ACBsin30°=.
[题后反思] (1) 熟练掌握正、余弦定理 ( http: / / www.21cnjy.com )的应用;(2) 测量角度,首先应明确方位角、方向角等含义;(3) 在解应用题时,首先分析题意,分清已知与所求,再根据题意正确画出示意图;(4) 解题时要注意体会正弦定理、余弦定理“联袂”使用的优点,同时注意三角函数知识在求解过程中的应用.
变式 一船自西向东匀速航行,上午10时 ( http: / / www.21cnjy.com )到达一座灯塔P南偏西75°的方向、距塔68n mile的M处,下午2时到达这座灯塔东南方向的N处,求这只船的航行速度.
(变式)
[规范板书] 解 如图,在△PMN中,由正弦定理得MN===34,∴ v==(n mile/h).即这只船的航行速度为n mile/h.
【例2】 在海岸A处,发现北偏东45°方向、距离A处(-1)n mile的B处有一艘走私船,若在A处北偏西75°方向、距离A处2n mile的C处的缉私船奉命以10n mile/h的速度追截走私船,此时,走私船正以10n mile/h的速度从B处向北偏东30°的方向逃跑,问:缉私船沿什么方向能最快追上走私船 [3]
(见学生用书课堂本P10)
[处理建议] 思路解析:本例考查了 ( http: / / www.21cnjy.com )正弦定理、余弦定理的建模应用.如图,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求出∠BCD.
[规范板书] 解 设缉私船用了th在D处追上走私船(如图),则有CD=10t,BD=10t.在△ABC中,AB=-1,AC=2,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=22+-2×2×(-1)×cos120°=6,∴ BC=.
( http: / / www.21cnjy.com )
(例2)
由正弦定理得sin∠ABC===,∴ ∠ABC=45°,∴ BC与正北方向垂直.
在△BCD中,∠CBD=90°+30°=120°,由正弦定理得sin∠BCD===,∴ ∠BCD=30°.∴ 缉私船沿北偏东60°的方向能最快追上走私船.
[题后反思] (1) 测量角度, ( http: / / www.21cnjy.com )首先应明确方位角、方向角等含义;(2) 在解应用题时,首先分析题意,分清已知与所求,再根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题时要注意体会正弦定理、余弦定理“联袂”使用的优点.
变式 如图,已知两座灯塔A和B与海洋观 ( http: / / www.21cnjy.com )察站C的距离相等,灯塔A在观察站C北偏东40°的方向上,灯塔B在观察站C南偏东60°的方向上,则灯塔A在灯塔B北偏西多少度的方向上
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 由已知得∠ACB ( http: / / www.21cnjy.com )=180°-40°-60°=80°,又AC=BC,∴ ∠A=∠ABC=50°,∠ABD=∠CBD-∠ABC=60°-50°=10°.∴ 灯塔A在灯塔B北偏西10°的方向上.
*【例3】 用同样高度的两个测角仪A ( http: / / www.21cnjy.com )B和CD分别测得正西方向上空的气球E的仰角是α和β.已知B,D间的距离为a,测角仪的高度是b,求气球的高度.[4]
( http: / / www.21cnjy.com )
(例3)
[处理建议] 在Rt△EGA中求解EG ( http: / / www.21cnjy.com ),只有角α一个条件,需要再有一边长被确定,而△EAC中有较多已知条件,故可在△EAC中考虑EA边长的求解,而在△EAC中有角β,∠EAC=180°-α与边AC=a,故可以利用正弦定理求解EA.
[规范板书] 解 在△ACE中,AC=BD=a,∠ACE=β,∠AEC=α-β,由正弦定理得AE==.
在Rt△AGE中,EG=AE·sinα=.
∴ EF=FG+GE=b+.
答:气球的高度是b+.
[题后反思] (1) 在 ( http: / / www.21cnjy.com )测量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内视线与水平线的夹角;(2) 准确理解题意,分清已知与所求,画出示意图;(3) 运用正(余)弦定理,有序地解相关的三角形,逐步求解问题的答案,注意等价转化思想的运用.
变式 你还能用其他方法求出气球的高度吗
[处理建议] 本题也可以通过解两个直角三角形来解决,思路如下:设EG=x,在Rt△EGA中,利用表示AG;在Rt△EGC中,利用表示CG,而CG-AG=CA=a,故可以求出EG,从而求出气球的高度EF.
四、 课堂练习
1. 设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sinA=5sinB,则角C=120°.
2. 地上画了一个角,即∠BDA ( http: / / www.21cnjy.com )=60°.某人从角的顶点D出发,沿角的一边DA行走10m后,拐弯往另一方向行走14m正好到达∠BDA的另一边BD上的一点,我们将该点记为E,则E与D之间的距离为16m.
提示 如图,设ED=xm ( http: / / www.21cnjy.com ),则由余弦定理得142=102+x2-2x·10cos60°,整理得x2-10x-96=0,解得x=16或x=-6(舍去).所以E与D之间的距离为16m.
( http: / / www.21cnjy.com )
(第2题)
3. 江岸边有一炮台高30m,江中 ( http: / / www.21cnjy.com )有两条船,由炮台顶部测得两船的俯角分别为45°和30°,若这两条船与炮台底部连线成30°角,则两条船相距30m.
提示 设炮台顶部为C,底部为O,两条船分别为A,B,在Rt△AOC与Rt△BOC中,OA=OC·tan45°=30×1=30,OB=OC·tan60°=30×=30.
在△OAB中,由余弦定理得AB2=OA2+OB2-2OA·OB·cos∠AOB=302+-2×30×30×cos30°=900,∴ AB=30.∴ 两条船相距30m.
五、 课堂小结
1. 通过本节课的学习,我们知 ( http: / / www.21cnjy.com )道正弦定理、余弦定理有着非常广泛的应用.如果我们抽去每个应用题中与生产、生活实际所联系的外壳,就暴露出解三角形问题的本质,这就需要我们在解决实际问题的过程中,不断提高分析问题和解决问题的能力,以及将实际问题转化为抽象的数学问题的能力.
2. 理解各种应用问题中的有关名词、术语,如坡度、俯角、仰角、方向角、方位角等.
第6课时 正弦定理、余弦定理的应用(2)
教学过程
一、 数学运用
在上一节课中,我们一起学习了正、余 ( http: / / www.21cnjy.com )弦定理在实际中的应用,了解了一些把实际问题转化为解三角形问题的方法,掌握了一定的解题方法与技巧;在这一节课中,我们将给出几个例题,请大家尝试用上一节课所学的方法加以解决.
【例1】 如图,为了测量河 ( http: / / www.21cnjy.com )对岸A,B两点间的距离,在所站这一岸定一基线CD,现已测出CD=a,∠ACD=α,∠BCD=β,∠BDC=γ,∠ADC=δ,试求AB的长.[2]
( http: / / www.21cnjy.com )
(例1)
(见学生用书课堂本P11)
[处理建议] (1) 先帮助学 ( http: / / www.21cnjy.com )生分析思路,然后让学生解决;(2) 如图,对于AB的求解,可以在△ABC中或者△ABD中求.若在△ABC中求解,由∠ACB=α-β,故需先求出AC,BC,再利用余弦定理求得,而AC可在△ACD中利用正弦定理求得,BC可在△BCD中利用正弦定理求得.
[规范板书] 解 在△ACD中,由正弦定理得AC===.
在△BCD中,由正弦定理得BC===.
在△ABC中,∠ACB=α-β,由余弦定理得AB=
.
[题后反思] (1) 熟练掌握正、余弦定理的应用;(2) 注意体会例1的求解过程在实际中的应用.
变式 直线AB外有一点C,∠ABC=60°, ( http: / / www.21cnjy.com )AB=200km,汽车甲以80km/h的速度由A向B行驶,同时摩托车乙以50km/h的速度由B向C行驶,问:运动开始几小时后,两车的距离最小
[规范板书] 解 设经过th后,两车相距skm,则由余弦定理得s2=(200-80t)2+(50t)2-2×(200-80t)×(50t)·cos60°=12900t2-42000t+40000.当t=≈1.6时,s最小.
答:运动开始约1.6h后,两车的距离最小.
【例2】 据气象台预报,距S岛正东方 ( http: / / www.21cnjy.com )向300km的A处有一台风中心形成,并正以30km/h的速度沿北偏西30°的方向移动,在距台风中心270km以内的地区将受到台风的影响.问:S岛是否受到台风影响 若受到影响,从现在起经过多少小时S岛开始受到台风的影响 持续时间多久 [3]
(见学生用书课堂本P12)
[处理建议] (1) 先 ( http: / / www.21cnjy.com )帮助学生分析思路,然后让学生解决;(2) 设B为台风中心,则B为AB边上的动点,SB也随之变化.S岛是否受台风影响可转化为SB≤270这一不等式是否有解的判断,则需表示出SB,可设台风中心经过th到达B点,则在△ABS中,由余弦定理可求出SB.
[规范板书] 解 设台风中心经过th到达B点,由题意得∠SAB=90°-30°=60°.
( http: / / www.21cnjy.com )
(例2)
在△ABS中,由余弦定理 ( http: / / www.21cnjy.com )得SB2=SA2+AB2-2SA·AB·cos∠SAB=3002+(30t)2-2×300×30tcos60°=900t2-9000t+90000.
若S岛受到台风影响,则应满足条件SB≤270,即SB2≤2702,化简整理得t2-10t+19≤0,解得5-≤t≤5+.所以从现在起,经过(5-)hS岛开始受到台风的影响,(5+)h后影响结束,持续时间为(5+)-(5-)=2(h).
答:S岛将受到台风的影响,从现在起经过(5-)h,台风开始影响S岛,且持续时间为2h.
[题后反思] 此题为探索性命题,可以 ( http: / / www.21cnjy.com )假设命题成立去寻求解存在的条件,也可假设命题不成立去寻求解存在的条件.本题求解过程采用了第一种思路(SB≤270是否有解最终转化为关于t的一元二次不等式是否有解,与一元二次不等式解法相联系).
变式 海中有一小岛B,周围3.8n m ( http: / / www.21cnjy.com )ile内有暗礁,军舰由西向东航行到A处,望见岛B在北偏东75°的方向上;军舰又航行了8n mile到达C处,望见岛B在北偏东60°的方向上.若此军舰不改变航向而继续前进,有无触礁危险
( http: / / www.21cnjy.com )
(变式)
[处理意见] 军舰继续向东航行,有无触礁 ( http: / / www.21cnjy.com )的可能取决于B到直线AC的距离是否大于3.8n mile.于是我们只要先算出BC(或AB)的大小,再算出B到直线AC的距离,将它与3.8n mile比较即可得到答案.
[规范板书] 解 在△ABC中,AC=8,∠A=15°,∠ACB=150°,∴ ∠B=15°,从而BC=AC=8.∴ B到直线AC的距离为BC·sin30°=8×=4>3.8.因此,军舰不改变航向而继续航行,没有触礁的危险.
*【例3】 如图,已知扇形AOB的圆心 ( http: / / www.21cnjy.com )角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.[4]
( http: / / www.21cnjy.com )
(例3)
[处理建议] (1) 先帮助学生分析思路,然 ( http: / / www.21cnjy.com )后让学生解决;(2) △POC的面积会随θ的变化而变化,所以要用θ表示△POC的面积,因此首先要用θ表示OC.
[规范板书] 解 ∵ CP∥OB,∴ ∠OCP=120°,∴ ∠CPO=60°-θ.在△POC中,由正弦定理得OC===sin(60°-θ).
因此,△POC的面积为S(θ)=OP·OC·sinθ=sin(60°-θ)sinθ=sin(2θ+30°)-.
∵ 0°<θ<60°,∴ 当θ=30°时,S(θ)取得最大值为.
[题后反思] 此题是通过解三角 ( http: / / www.21cnjy.com )形来建立函数关系,然后利用三角函数的性质来求最值,这种通过建立函数模型来求最值是高考中常考的题型,提醒学生注意.
变式 如图,已知半圆的直径AB=2 ( http: / / www.21cnjy.com ),点C在AB的延长线上,BC=1,P为半圆上的一个动点,以PC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 设∠POB ( http: / / www.21cnjy.com )=θ,四边形OPDC的面积为y.在△POC中,由余弦定理得PC2=OP2+OC2-2·OP·OC·cos∠POC=5-4cosθ.
∴ y=S△POC+S△PCD=×2×1×sinθ+(5-4cosθ)=2sin+.
∵ 0≤θ≤π,∴ -≤θ-≤π,∴ 当θ-=,即θ=时,ymax=2+.∴ 四边形OPDC面积的最大值为2+.
二、 课堂练习
1. 在塔底所在水平面上的某点测得塔顶的仰角为θ,由此点向塔沿直线行走30m,测得塔顶的仰角为2θ,再向塔继续前进10m,又测得塔顶的仰角为4θ,则塔高是15m.
2. 某人沿正东方向走xkm后,向右转150°,然后朝新的方向走3km,结果他离出发点恰好 km,则x=或2.
提示 由题意可得cos30°=,化简得x2-3x+6=0,解得x=或x=2.
3. 如图,为了测量隧道AB的长度,给定下列四组数据,则测量应当选用数据③ .(填序号)
① α,a,b; ② α,β,a; ③ a,b,γ; ④ α,β,γ.
( http: / / www.21cnjy.com )
(第3题)
三、 课堂小结
1. 通过本节课的学习,我们知道正弦定理、 ( http: / / www.21cnjy.com )余弦定理有着非常广泛的应用.如果我们抽去每个应用题中与生产生活实际所联系的外壳,就暴露出解三角形问题的本质,这就需要我们在解决实际问题的过程中,不断提高分析问题和解决问题的能力,以及将实际问题转化为抽象的数学问题的能力.
2. 理解各种应用问题中的有关名词、术语,如坡度、俯角、仰角、方向角、方位角等.
3. 注意不等式、函数等代数知识的引入与应用.
第7课时 本章复习(1)
教学过程
一、 知识梳理
1. 正弦定理、余弦定理
定理 正弦定理 余弦定理
内容 ===2R. a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.
变形形式 a=2RsinA,b=2RsinB,c=2RsinC;a∶b∶c=sinA∶sinB∶sinC. cosA=,cosB=,cosC=.
作用 1. 已知两角和任一边,求另一角和其他两边;2. 已知两边和其中一边的对角,求另一边和其他两角. 1. 已知三边,求三个角;2. 已知两边和它们的夹角,求第三边和其他两个角.
2. 在△ABC中,已知a,b和A时,角B解的情况如下表:
A为锐角 A为钝角或直角
图形 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) (a>b情形的图形)
满足条件 a
角B解的情况 无解 一解 两解 一解 一解 无解
3. 三角形中一些常用的结论:
(1) S△ABC=acsinB=bcsinA=absinC==r(a+b+c).(其中R,r分别为△ABC的外接圆和内切圆的半径)
(2) A>B a>b sinA>sinB.
二、 数学运用
正弦定理、余弦定理的应用包括两大方面:一是 ( http: / / www.21cnjy.com )数学内部的应用;二是实际应用.那么,正弦定理、余弦定理能解决数学内部哪些方面的问题呢 下面我们来看一看在三角形中的运用.
(一) 求解三角形中的基本元素
【例1】 在△ABC中,已知a=2, c=+, B=45°, 求b及A[1].
(见学生用书课堂本P13)
[处理建议] 引导学生审题,根据条件,已知a ( http: / / www.21cnjy.com ), c及其夹角B,自然想到先用余弦定理求出b;对于角A,可以利用余弦定理求得,也可以利用正弦定理求得.
[规范板书] ∵ b2=a2+c2-2accosB
=(2)2+(+)2-2×2×(+)×cos45°
=12+(+)2-4×(+1)
=8,
∴ b=2.
求A可以利用余弦定理,也可以利用正弦定理:
解法一 ∵ cosA=
==, 又∵A∈(0°, 180°), ∴ A=60°.
解法二 ∵ sinA=sinB=×sin45°=, 又∵ +>2.2+1.4=3.6, 2<2×1.8=3. 6, ∴ a
变式 已知某三角形的三边的长是三个连续的整数,最大角是最小角的2倍,求此三角形的最小边的长.
[处理建议] 设最小边的长为a ( http: / / www.21cnjy.com ),则另两边的长分别为a+1, a+2,三边长中只有一个未知量;设最小角为α,则最大角为2α,另一角为π-3α,三个角中也只有一个未知量,因此,只要建立两个方程就可求解.
[规范板书] 解 设最小边的长为a,最小角为α, 由正弦定理知=,得cosα=; 由余弦定理知cosα==, 解得a=4,所以最小边的长是4.
(二) 判断三角形的形状
【例2】 在△ABC中,若=,试判断△ABC的形状.[2] (见学生用书课堂本P13)
[处理建议] 三角形形状的判断方法是首先边化角或角化边,再整理化简即可判断.
[规范板书] 解法一 = = = sinAcosA=sinBcosB sin2A=sin2B 2A=2B或2A+2B=180°,即有A=B或A+B=90°.从而有A=B或C=90°,所以△ABC为等腰三角形或直角三角形.
解法二 = = = = acosA=bcosB a·=b· a2(b2+c2-a2)=b2(c2+a2-b2) (a2-b2)(a2+b2-c2)=0,即有a2=b2或a2+b2=c2,所以△ABC为等腰三角形或直角三角形.
[题后反思] (1) 依据已知条件中的边角关 ( http: / / www.21cnjy.com )系判断三角形的形状时,主要有如下两种方法:① 利用正(余)弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;② 利用正(余)弦定理把已知条件转化为三角形内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用A+B+C=π这个结论.
(2) 注意在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
变式 在△ABC中,已知角A,B均为锐角,且cosA>sinB,试判断△ABC的形状.
[规范板书] 解 因为角A,B均为锐角,所以-A,B都是锐角.因为cosA>sinB,所以cosA=sin>sinB,则-A>B,即A+B<,所以C>,所以△ABC为钝角三角形.
(三) 三角形中的证明问题
【例3】 已知△ABC,证明:-=-.[3] (见学生用书课堂本P14)
[处理建议] 三角形中同时 ( http: / / www.21cnjy.com )含有边和角的等式的证明,通常要用正(余)弦定理进行边角归一,一是归为边的代数恒等式的证明,二是归为角的三角恒等式的证明.
[规范板书] 证明 左边=-=-=-=-=右边.故原命题得证.
变式 已知△ABC,证明:(a2-b2-c2)tanA+(a2-b2+c2)tanB=0.
[规范板书] 证明 左边=(a2-b2-c2)+(a2-b2+c2)=(a2-b2-c2)··+(a2-b2+c2)··=·(a2-b2-c2)·+·(a2-b2+c2)·=-+=0=右边.故原命题得证.
[题后反思] (1) 例3 ( http: / / www.21cnjy.com )的证明过程中用到了余弦二倍角公式,而此公式有三种形式(cos2A=cos2A-sin2A,cos2A=2cos2A-1,cos2A=1-2sin2A),由于考虑到等式右端为边的关系,故选用第三种形式,在转化为边的关系时较为简便.(2) 在变式题证明时应注意两点:一是切化弦的思路,二是结合正、余弦定理将角的关系转化为边的关系.
(四) 三角形中的求值问题
【例4】 在△ABC中,已知c=2,C=.
(1) 若△ABC的面积等于,求a,b;
(2) 若sinC+sin(B-A)=2sin2A,求△ABC的面积.[4] (见学生用书课堂本P14)
[处理建议] 主要是利用正、余弦定理,并结合三角形的面积公式来解题.
[规范板书] 解 (1) 由题意得a2+b2-ab=4,absinC=,所以ab=4,联立方程组解得
(2) 由题意得sin(B+A)+s ( http: / / www.21cnjy.com )in(B-A)=4sinAcosA,即sinBcosA=2sinAcosA,即cosA(sinB-2sinA)=0.
当cosA=0时,A=,B=,a=,b=;
当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a,联立方程组解得
所以△ABC的面积S=absinC=.
[题后反思] (1) 对于三角形中的求值 ( http: / / www.21cnjy.com )问题,主要是利用正、余弦定理,并结合三角形的面积公式来解题;除此之外,更要善于利用方程思想来解题.(2) 可将第二小题作为变式让学生练习,让他们体会方程思想的应用.
(五) 正、余弦定理在几何中的应用
*【例5】 如图,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°,求BD的长.[5]
(例5)
[处理建议] 帮助学生分析思路:① ( http: / / www.21cnjy.com ) 由于AB=5,∠ADB=45°,因此要求BD,可在△ABD中,通过正弦定理求解,关键是确定∠BAD的正弦值;② 在△ABC中,AB=5,AC=9,∠BCA=30°,因此可利用正弦定理求出sin∠ABC,再依据∠ABC与∠BAD互补,确定sin∠BAD即可.
[规范板书] 解 在△ABC中,由正弦定理得sin∠ABC===.
∵ AD∥BC,∴ ∠BAD=180°-∠ABC,∴ sin∠BAD=sin∠ABC=.
在△ABD中,由正弦定理得BD===.
[题后反思] 正、余弦定理在几何中 ( http: / / www.21cnjy.com )的应用:① 首先根据已知量和未知量确定未知量所在的三角形;② 其次确定与未知量相关联的量;③ 最后把要求解的问题转化到由已知条件可直接求解的量上来.
( http: / / www.21cnjy.com )
(变式)
变式 如图,我炮兵阵地位于A ( http: / / www.21cnjy.com )处,两观察所分别设于B,D处,已知△ABD是边长等于a的正三角形,当目标出现于C处时,测得∠BDC=45°,∠CBD=75°,求炮击目标的距离AC.
[规范板书] 解 在△BCD中,由正弦定理得=,∴ BC=a.在△ABC中,由余弦定理得AC2=+a2-2×a·a·cos135°=a2,∴ AC=a.
答:炮击目标的距离AC为a.
三、 课堂练习
1. 在△ABC中,若A=60°,b=1,S△ABC=,则a=.
提示 S△ABC= bcsinA=×1·csin60°=c=,∴ c=4,从而a2=b2+c2-2bccosA=1+16-4=13,∴ a=.
2. 若△ABC的三个内角满足sinA∶sinB∶sinC=5∶11∶13,则△ABC的形状为钝角三角形.
提示 由正弦定理可得a∶b∶c=5∶11∶13.设a=5t,b=11t,c=13t,由余弦定理得cosC===-<0,所以C为钝角,故△ABC为钝角三角形.
3. 在△ABC中,已知=.
(1) 求的值;
(2) 若cosB=,b=2,求△ABC的面积S.
解 (1) =可化为=,即cosAsinB-2cosCsinB=2sinCcosB-sinAcosB,则cosAsinB+sinAcosB=2sinCcosB+2cosCsinB,所以sin(A+B)=2sin(C+B).而A+B+C=π,则sinC=2sinA,即=2.(也可以尝试用余弦定理来处理)
(2) 由(1)得c=2a,由余弦定理得4=c2+a2-2accosB=4a2+a2-a2=4a2,所以a=1,c=2.S=acsinB=×1×2×=.
四、 课堂小结
掌握利用正、余弦定理解决三角形内部问题的常见题型的处理方法和技巧.
第8课时 本章复习(2)
教学过程
一、 知识梳理
实际应用问题的处理方法和步骤归纳:
(1) 一般步骤:
① 分析:理解题意,分清已知与未知,画出示意图;
② 建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解三角形的数学模型;
③ 求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;
④ 检验:检验上述所求的解是否具有实际意义,从而得出实际问题的解.
(2) 实际应用问题常有以下几种情形:
① 实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解;
② 实际问题经抽象概括后,已知量与未知量涉及两个三角形或多个三角形,这时需按顺序逐步在几个三角形中求出问题的解;
③ 实际问题经抽象概括后,涉及的三角形只有一个,但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.
二、 数学运用
正弦定理、余弦定理的应用包括两大 ( http: / / www.21cnjy.com )方面:一是数学内部的应用;二是实际应用.那么,正弦定理、余弦定理能解决实际应用中哪些方面的问题 下面我们来看一看在实际应用问题中的运用.
(一) 与距离有关的问题
【例1】 如图,A,B,C,D都在同 ( http: / / www.21cnjy.com )一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.在水面A处的船上测得B,D两点的仰角分别为75°和30°,在水面C处的船上测得B,D两点的仰角均为60°,AC=0.1km.
( http: / / www.21cnjy.com )
(例1)
(1) 求证:AB=BD.
(2) 求BD的长.[1] (见学生用书课堂本P15)
[处理建议] 思路解析:(1) 由已 ( http: / / www.21cnjy.com )知角度不难求得∠BCD,且易得AC=DC关系,利用三角形全等可得AB=BD;(2) 求BD只需将其转化在某个三角形中利用已知条件即可求.
[规范板书] 证明 (1) 在△A ( http: / / www.21cnjy.com )CD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,∴ CD=AC.又∠BCD=180°-60°-60°=60°,∴ ∠BCD=∠BCA,∴ △ACB≌△DCB.∴ BD=BA.
(2) 在△ABC中,由正弦定理得AB===,∴ BD=AB=(km).
[题后反思] (1) 要让学生熟练掌握正、余弦定理的应用;(2) 注意平面几何知识在求解过程中的应用.
变式 如图,公路MN和PQ在P处交汇 ( http: / / www.21cnjy.com ),且∠QPN=30°,在A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响 请说明理由;如果学校受到影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少
(变式)
[规范板书] 解 作AB⊥MN,垂足为B.在Rt△ABP中,∵ ∠ABP=90°,∠APB=30°,∴ AB=PA=80(m).∵ 点A到直线MN的距离小于100m,所以这所中学会受到噪声的影响.
如图,若以A为圆心、100m长为半径画圆,那么☉A和直线MN有两个交点,设交点分别为C,D,连结AC和AD,则AC=AD=100m.根据勾股定理和垂径定理得CD=2CB=2=120(m),∴ 学校受到噪声影响的时间为×3600=24(s).
(二) 与高度有关的问题
【例2】 某人在山顶观察地面上相距 ( http: / / www.21cnjy.com )2500m的A,B两个目标,测得A在南偏西57°的方向上,俯角为30°,同时测得B在南偏东78°的方向上,俯角是45°,求山高.(设A,B与山底在同一平面上,计算结果精确到0.1m)[2] (见学生用书课堂本P15)
[处理建议] 让学生分析 ( http: / / www.21cnjy.com )思路:(1) 在Rt△APQ和Rt△BPQ中,用高表示AQ,BQ;(2) 在斜△ABQ中,利用余弦定理建立方程,解出高.
[规范板书] 解 画出示意图(如图).
( http: / / www.21cnjy.com )
(1)
( http: / / www.21cnjy.com )
(2)
(例2)
设山高PQ=h,则在Rt△APQ和Rt△BPQ(如图(1))中,AQ==h,BQ==h.
在斜△ABQ(如图(2))中,∠AQB=57°+78°=135°,所以由余弦定理得AB2=AQ2+BQ2-2·AQ·BQ·cos∠AQB,即25002=+h2-2·h·h·cos135°,解得h=≈984.4(m).
所以山高约984.4m.
[题后反思] (1) 在测 ( http: / / www.21cnjy.com )量高度时,要理解仰角、俯角的概念,仰角和俯角都是在同一铅垂面内视线与水平线的夹角;(2) 准确理解题意,分清已知与所求,画出示意图;(3) 运用正、余弦定理,有序地解相关的三角形,逐步求解问题的答案,注意方程思想的运用.
变式 如图,测量河对岸的塔高AB ( http: / / www.21cnjy.com )时,可以选与塔底B在同一水平面内的两个观测点C与D.现测得∠BCD=75°,∠BDC=60°,CD=s,并在点C处测得塔顶A的仰角为30°,求塔高AB.
( http: / / www.21cnjy.com )
(变式)
[规范板书] 解 在△BCD中,∠CBD=180°-(75°+60°)=45°,由正弦定理得BC===s.在Rt△ABC中,AB=BC·tan30°=s.所以塔高AB为s.
(三) 与角度有关的问题
【例3】 在海岸A处,发现北偏西75°的方向、距离A处2n mile的B处有一艘走私船,若在A处北偏东45°的方向、距离A处(-1)n mile的C处的缉私船奉命以10n mile/h的速度追截走私船,此时,走私船正以10n mile/h的速度从B处沿北偏西30°的方向逃窜,问:缉私船沿什么方向才能最快追上走私船 所需时间为多少 [3] (见学生用书课堂本P16)
[处理建议] 思路解析:本例考查了 ( http: / / www.21cnjy.com )正弦定理、余弦定理的建模应用.如图所示,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求∠BCD.
[规范板书] 解 设xh后,它们在D处相遇,则CD=10xn mile,BD=10xn mile,∠CBD=120°.
( http: / / www.21cnjy.com )
(例3)
在△ABC中,AB=2,AC=-1,∠BAC=120°,由余弦定理得BC2=AB2+AC2-2AB·AC·cos∠BAC=22+-2×2×(-1)×cos120°=6,∴ BC=.
而sin∠ACB===,∴ ∠ACB=45°,∴ BC与正北方向垂直.
在△BCD中,∠CBD=90°+30°=120°,由余弦定理得CD2=BC2+BD2-2BC·BD·cos∠CBD,即=+(10x)2-2××10x·cos120°,整理得200x2-10x-6=0,解得x=或x=-(舍去).
因此,在△BCD中,BD=,CD=3,∠CBD=120°.由正弦定理得sin∠BCD===,∴ ∠BCD=30°.
∴ 缉私船沿北偏西60°的方向才能最快追上走私船,所需时间为h.
[题后反思] (1) 测量角度,首先 ( http: / / www.21cnjy.com )应明确方位角、方向角等含义;(2) 在解应用题时,应先分析题意,分清已知与所求,再根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题,解题中要注意体会正、余弦定理“联袂”使用的优点.
变式 如图,已知海中一小岛A周围3 ( http: / / www.21cnjy.com )8n mile内有暗礁,一船正在向南航行,在B处测得小岛A在船的南偏东30°的方向上,船航行30n mile后,在C处测得小岛A在船的南偏东45°的方向上,如果此船不改变航向,继续往南航行,有无触礁的危险
( http: / / www.21cnjy.com )
(变式)
[处理建议] 船继续向南航行,有无触礁 ( http: / / www.21cnjy.com )的可能取决于A到直线BC的距离是否大于38n mile.于是我们只要先算出AC(或AB)的大小,再算出A到直线BC的距离,将它与38n mile比较即可得到答案.
[规范板书] 解 在△ABC中,BC=30,∠B=30°,∠ACB=135°,∴ ∠A=15°.由正弦定理得=,即=,∴ AC==15(+).
∴ A到直线BC的距离为AC·sin45°=15(+1)≈40.98(n mile),它大于38n mile,因此船不改变航向,继续向南航行,没有触礁的危险.
四、 课堂练习
1. 如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,则AB边的长为5.
(第1题)
2. 已知锐角△ABC的内角A,B,C的对边分别为a,b,c,若23cos2A+cos2A=0,a=7,c=6,则b=5.
3. 某人在C点测得某塔在南偏 ( http: / / www.21cnjy.com )西80°的方向上,塔顶仰角为45°,此人沿南偏东40°的方向前进10m到达D点,测得塔顶A的仰角为30°,求塔高.
解 如图,设塔高为h,在Rt△ACO中,∵ ∠ACO=45°,则OC=OA=h.
在Rt△ADO中,∵ ∠ADO=30°,则OD=h.
在△OCD中,∠OCD=80°+40°=120°,CD=10,由余弦定理得OD2=OC2+CD2-2·OC·CD·
cos∠OCD,即(h)2=h2+102-2h×10×cos120°,整理得h2-5h-50=0,解得h=10或h=-5(舍去).
答:塔高为10m.
( http: / / www.21cnjy.com )
(第3题)
五、 课堂小结
有关斜三角形的实际问题,其解题的一般步骤是:
(1) 准确理解题意,分清已知与所求,尤其要理解应用题中的有关名词和术语;
(2) 画出示意图,并将已知条件在图形中标出;
(3) 分析与所研究问题有关的一个或几个三角形,合理运用正弦定理和余弦定理求解.
