18.1.1 平行四边形的定义及性质(共3课时)课件
文档属性
| 名称 | 18.1.1 平行四边形的定义及性质(共3课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-21 21:33:35 | ||
图片预览




文档简介
课件57张PPT。§18.1 .1
平行四边形
定义、性质(1)1、理解什么是平行四边形及其表示方法;
2、探索平行四边形的性质;
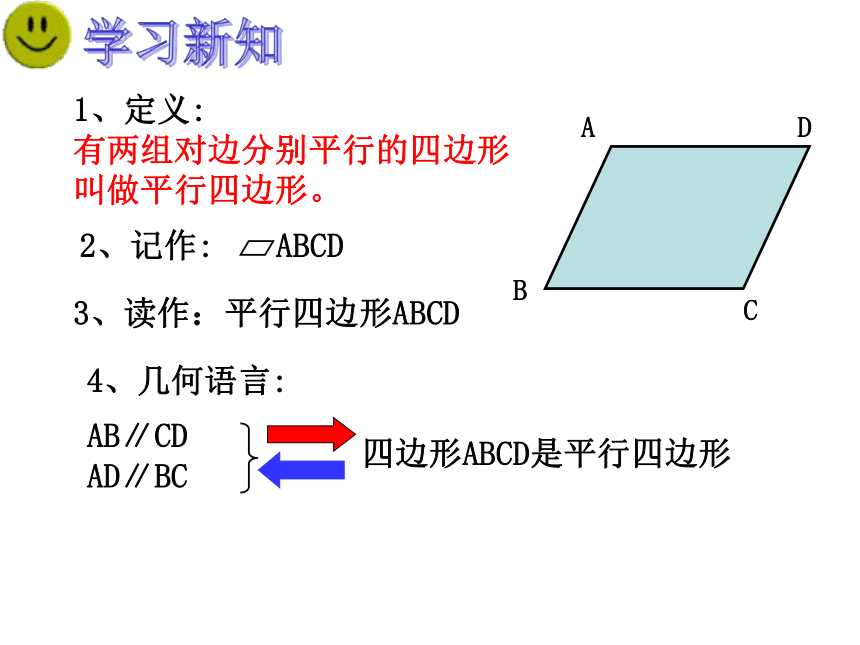
3、能利用平行四边形的性质解决问题。学习目标:学习重点:平行四边形的性质探究.学习难点:应用平行四边形的性质解决问题。 小学阶段你学习过哪些四边形?你能画图表示它们之间的关系吗?学习新知1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、记作:ABCD
3、读作:平行四边形ABCD4、几何语言:
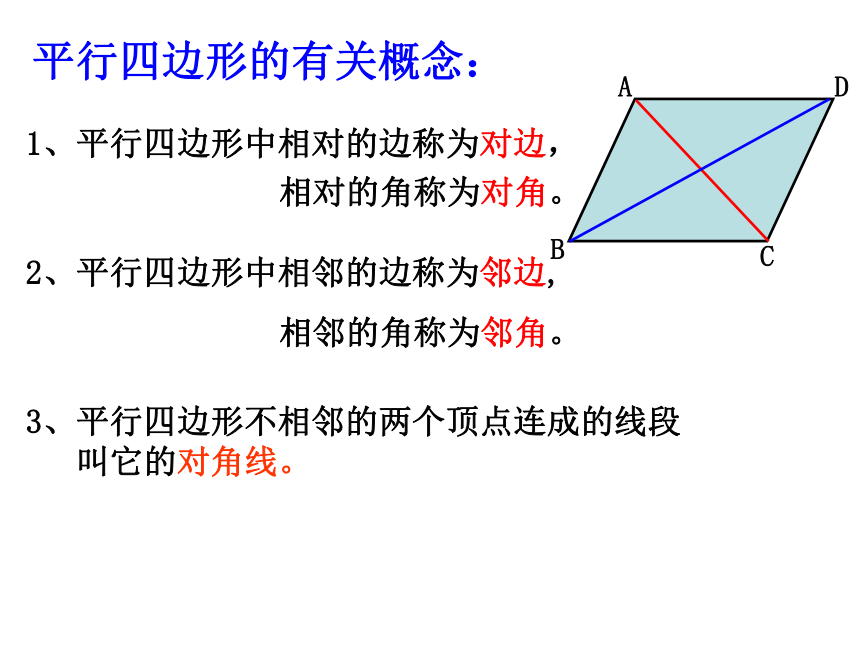
四边形ABCD是平行四边形AB∥CD AD∥BCABCDABCD1、平行四边形中相对的边称为对边,
相对的角称为对角。2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。平行四边形的有关概念:3、平行四边形不相邻的两个顶点连成的线段
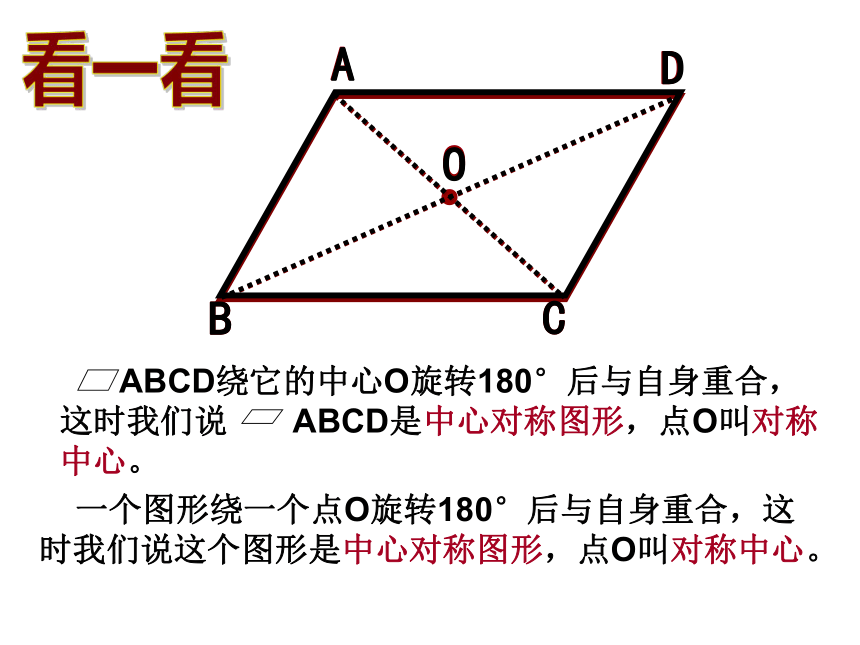
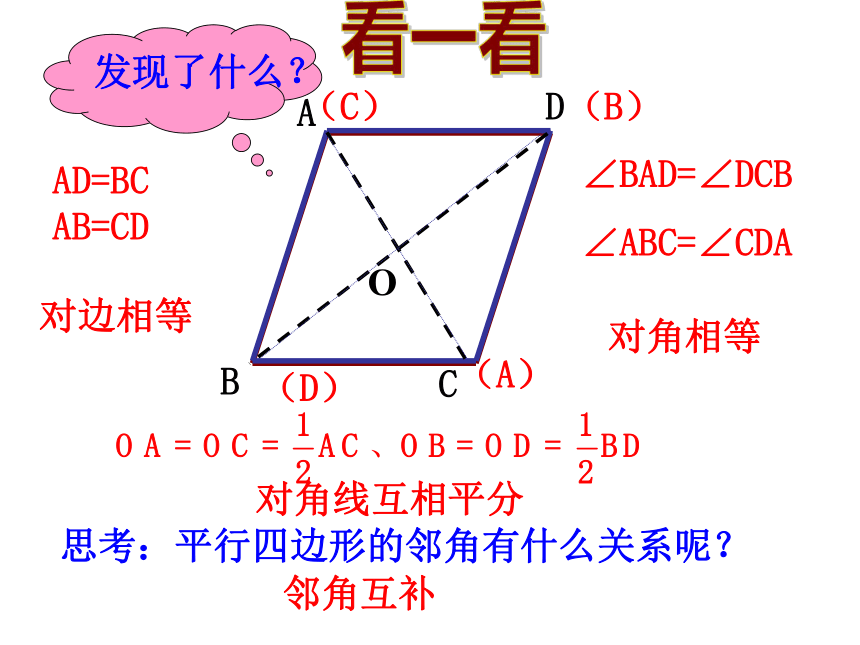
叫它的对角线。2、 平行线的判定方法有哪些?1、平行线有哪些性质???(1)两直线平行,同位角相等、内错角相等、同旁内角互补。(2)平行公理:经过直线外一点有且只有一条直线与已知直线平行。(2)同位角相等,两直线平行。(3)内错角相等,两直线平行。(4)同旁内角互补,两直线平行。(5)平行于同一条直线的两条直线平行。(6)垂直于同一条直线的两条直线平行。(1)根据定义:在同一平面内,不相交的两条直线是平行线(不常用)看一看 ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心。 一个图形绕一个点O旋转180°后与自身重合,这时我们说这个图形是中心对称图形,点O叫对称中心。 OABCD(C)(A)(B)(D)AD=BC AB=CD∠BAD=∠DCB
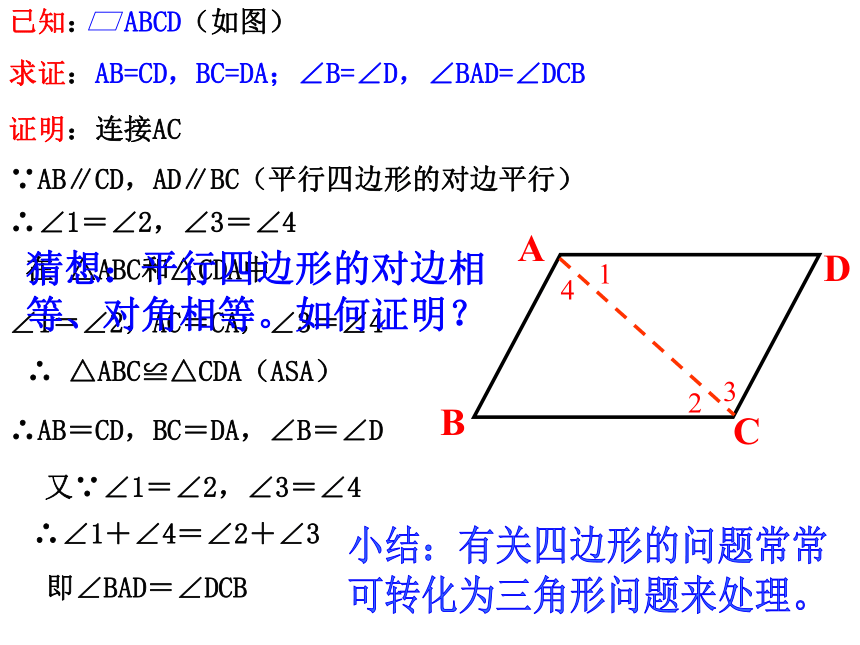
∠ABC=∠CDA思考:平行四边形的邻角有什么关系呢?对边相等对角相等对角线互相平分邻角互补发现了什么?看一看●O即∠BAD=∠DCB证明:连接AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在 △ABC和△CDA中ABCD小结:有关四边形的问题常常
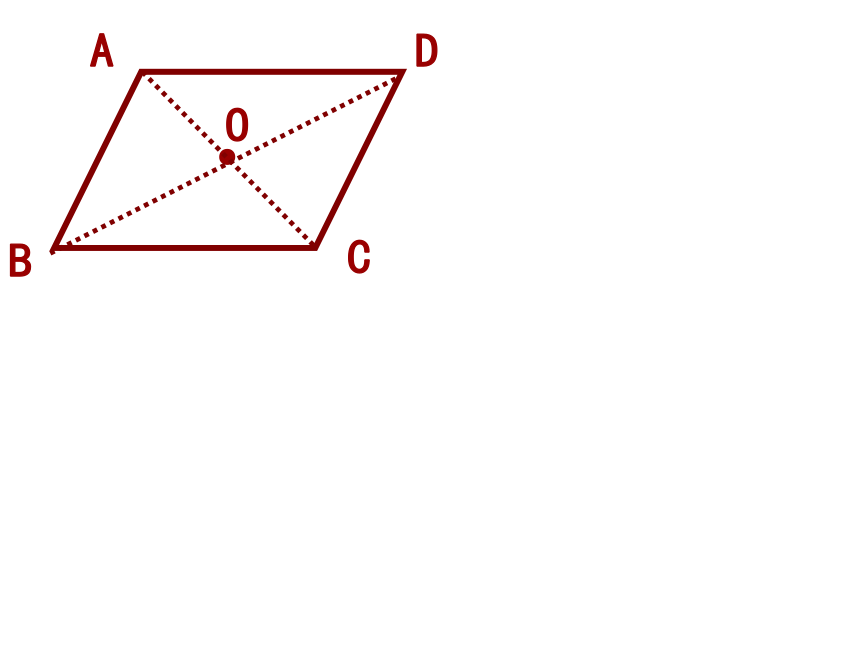
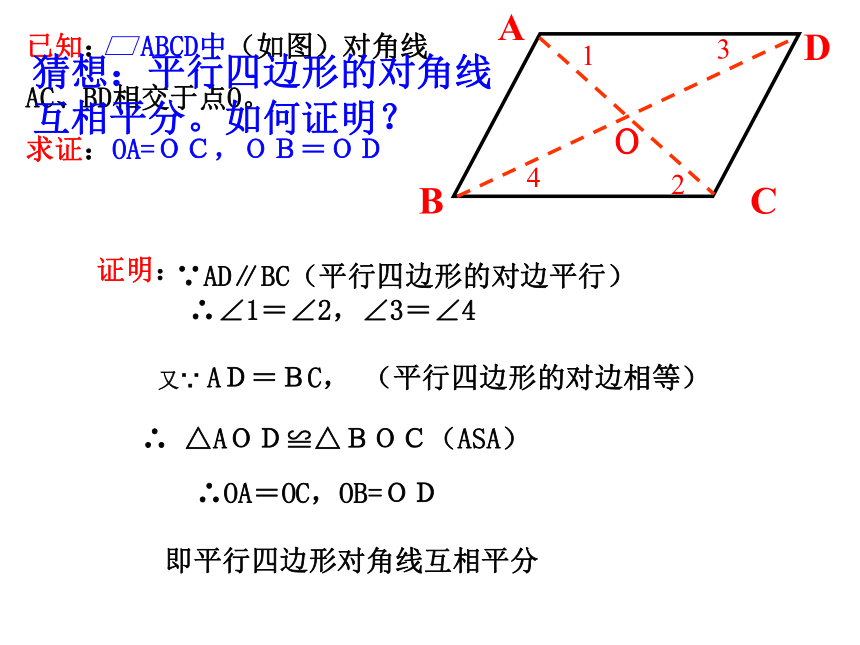
可转化为三角形问题来处理。猜想:平行四边形的对边相等、对角相等。如何证明?证明:∵AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4又∵ AD=BC,∴ △AOD≌△BOC(ASA)(平行四边形的对边相等)∴OA=OC,OB=ODABCD猜想:平行四边形的对角线互相平分。如何证明?O即平行四边形对角线互相平分平行四边形的性质1:平行四边形的对边平行且相等;平行四边形的对角相等;邻角互补。
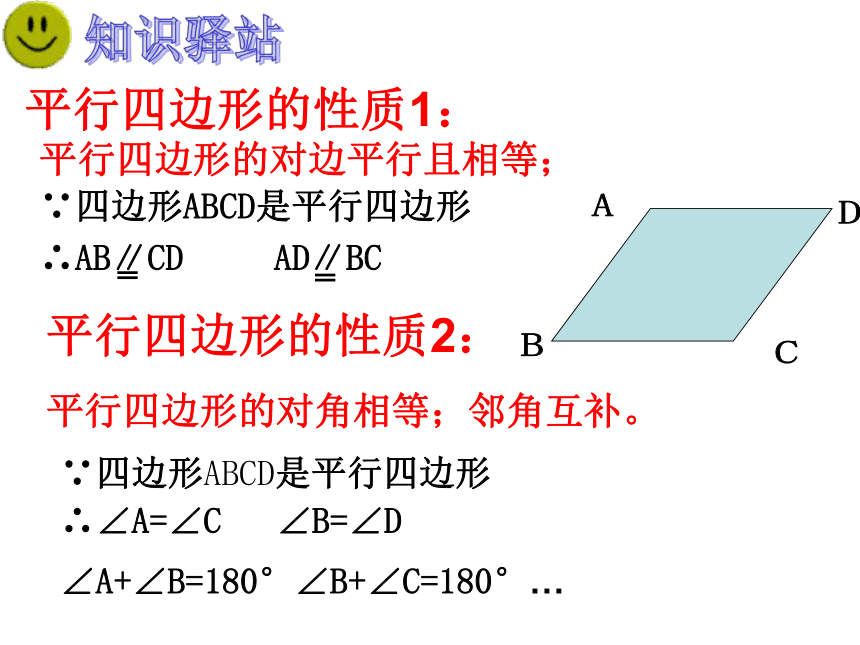
知识驿站平行四边形的性质2:∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠B=180°∠B+∠C=180°…平行四边形的对角线互相平分平行四边形的性质3:AC=BD吗? 1、已知一个平行四边形的两个内角之比为
1︰2,你能求出平行四边形每个内角的度数吗?新知应用小结:平行四边形中已知两个内角的度数比可求出每一个内角的度数。解:∵四边形ABCD是平行四边形
∴∠A+∠B=180° ∠A=∠C ∠B=∠D又∵∠A :∠B=1:2∴∠B= 2∠A∴∠A+2∠A=180°∴∠A=60°∴∠B=120°∴∠C=∠A=60° ∠D=∠B=60°2、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?ABCD解:四边形ABCD是平行四边形新知应用小结:平行四边形两邻边的和等于周长的一半。§18.1 .1
平行四边形
性质(2)平行四边形有哪些性质?1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心是对角线的交点。
5、周长=两邻边之和×2
6、面积=底边×底边上的高
概念应用
如图: ABCD中,EF∥AB
若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
ABDCEFGH9O选择:平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度B例1:如图,在 ABCD中ABCD1.基础知识:若∠A=130 ° ,则∠B=______ 、∠C=______ 、∠D=______2.变式训练: a、若∠A+ ∠C= 200 ° ,则∠A=______ 、 ∠B=______
b、若∠A:∠B= 5:4,则∠C=______ 、∠D=______50 °130 °50 °100 °80 °100 °80 °EF3.拓展延伸:若AE、AF为BC、CD边上的高,且∠EAF=60°则∠C = ——
∠B=——.
120 °60 °例2 如图1 ABCD中AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____441例3 如图2 , ABC,AB=AC=10,则 ADEF的周长为_____ABCDEF20例4 如图3 ABCD中,BC=5,AC=4,∠BAC=90.则 ABCD 的面积为 _____ABCD12图1图2图31、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .又若AB=13厘米,则△COD的周长为 。(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。2.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 209cm12cm34cm36cmD练一练练一练3、有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长为18cm?为什么?若平行四边形的一边长为xcm,则x的取值范围为多少?3cm<x<17cm练一练4、已知O是 ABCD两条对角线的交点,若已知AB=5,△OAB的周长比△OBC的周长短3,则BC=____ 82cm或8cm ABCD的周长为44cm, 对角线AC、BD相交于
O, 且△AOD的周长比△AOB的周长少2cm,
求 ABCD各边的长.
6、已知如图,在 ABCD中, E、F分别是边BC和AD上的点,且BE=DF。求证:①△ABE≌△CDF
②AE=CFABCDEF小结:运用平行四边形的性质可证明线段、角相等或三角形全等。新知应用7、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DFABCDOEF证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )两直线平行,内错角相等平行四边形的对角线互相平分SAS全等三角形的对应边相等5、已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DFABCDEF ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积ABCDE解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 ° ∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)试一试如图,已知平行四边形ABCD,以一组对边AD、BC向形外作等边△ADE和等边△ BCF,连结BE、DF,探索BE、DF的大小关系。挑战自我 已知平面上任意三点A、B、C,是否存在一点D,使A、B、C、D四点围成一个平行四边形。若存在,请你作出图形;若不存在,请说明理由。2018年12月16日星期日39如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )xYCO (0,0)B(5,0)D(2,3)A. (3,7) B. (5,3)
C. (7,3) D. (8,2)C§18.1 .1
平行四边形
性质(3)平行四边形有哪些性质?1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心是对角线的交点。
5、周长=两邻边之和×2
6、面积=底边×底边上的高
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°CAC如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °ABCDED6860°66 1.夹在两条平行线间的平行线段相等.
2.两条平行线间的距离处处相等.ABA′B′AB、A‘B’:夹在两条平行线间的平行线段.
CD、C‘D’:夹在两条平行线间的垂线段.CDC′D′两条平行线间的距离:两条平行线中,一条平行线上的点到另一条直线的距离,叫做两条平行线之间的距离。练一练:利用面积相等求两平行线间的距离10解:∵ AC⊥BC∴BC2=AB2-AC2=25=16=9(勾股定理)∴ BC=3∵ 四边形ABCD是平行四边形∴CE= AC=2,BD=2BE∴∴BD=2BE=(平行四边形对角线互相平分)(勾股定理)你还有别的方法吗?(1)△ABE的面积为 ______cm226练一练:4利用三角形面积求两平行线间的距离(2)若AB=4cm,则AB和DE间的
距离为 _____cm2 如图,E是直线CD上的一点。已知平行四边形ABCD的面积为52cm2,134如图, □ ABCD的两条对角线相交于点O.
(1)图中有多少对全等三角形?
请把它们写出来;
(2)图中有多少对面积相等的
三角形? 有一块平行四边形的草地,学校想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?想一想有无数种分法,分割线只要过对角线的交点 ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F.
求证:OE=OF巩固新知请判断下列图中,OE=OF还成立么? 过对角线交点的任一条直线都将平行四边形分成面积相等的两部分。4、一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗? O练一练MADBNQCP1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点P、Q,求证:MQ=NP
平行四边形
定义、性质(1)1、理解什么是平行四边形及其表示方法;
2、探索平行四边形的性质;
3、能利用平行四边形的性质解决问题。学习目标:学习重点:平行四边形的性质探究.学习难点:应用平行四边形的性质解决问题。 小学阶段你学习过哪些四边形?你能画图表示它们之间的关系吗?学习新知1、定义:
有两组对边分别平行的四边形 叫做平行四边形。2、记作:ABCD
3、读作:平行四边形ABCD4、几何语言:
四边形ABCD是平行四边形AB∥CD AD∥BCABCDABCD1、平行四边形中相对的边称为对边,
相对的角称为对角。2、平行四边形中相邻的边称为邻边,
相邻的角称为邻角。平行四边形的有关概念:3、平行四边形不相邻的两个顶点连成的线段
叫它的对角线。2、 平行线的判定方法有哪些?1、平行线有哪些性质???(1)两直线平行,同位角相等、内错角相等、同旁内角互补。(2)平行公理:经过直线外一点有且只有一条直线与已知直线平行。(2)同位角相等,两直线平行。(3)内错角相等,两直线平行。(4)同旁内角互补,两直线平行。(5)平行于同一条直线的两条直线平行。(6)垂直于同一条直线的两条直线平行。(1)根据定义:在同一平面内,不相交的两条直线是平行线(不常用)看一看 ABCD绕它的中心O旋转180°后与自身重合,这时我们说 ABCD是中心对称图形,点O叫对称中心。 一个图形绕一个点O旋转180°后与自身重合,这时我们说这个图形是中心对称图形,点O叫对称中心。 OABCD(C)(A)(B)(D)AD=BC AB=CD∠BAD=∠DCB
∠ABC=∠CDA思考:平行四边形的邻角有什么关系呢?对边相等对角相等对角线互相平分邻角互补发现了什么?看一看●O即∠BAD=∠DCB证明:连接AC∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∠1=∠2,AC=CA,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在 △ABC和△CDA中ABCD小结:有关四边形的问题常常
可转化为三角形问题来处理。猜想:平行四边形的对边相等、对角相等。如何证明?证明:∵AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4又∵ AD=BC,∴ △AOD≌△BOC(ASA)(平行四边形的对边相等)∴OA=OC,OB=ODABCD猜想:平行四边形的对角线互相平分。如何证明?O即平行四边形对角线互相平分平行四边形的性质1:平行四边形的对边平行且相等;平行四边形的对角相等;邻角互补。
知识驿站平行四边形的性质2:∵四边形ABCD是平行四边形
∴∠A=∠C ∠B=∠D
∠A+∠B=180°∠B+∠C=180°…平行四边形的对角线互相平分平行四边形的性质3:AC=BD吗? 1、已知一个平行四边形的两个内角之比为
1︰2,你能求出平行四边形每个内角的度数吗?新知应用小结:平行四边形中已知两个内角的度数比可求出每一个内角的度数。解:∵四边形ABCD是平行四边形
∴∠A+∠B=180° ∠A=∠C ∠B=∠D又∵∠A :∠B=1:2∴∠B= 2∠A∴∠A+2∠A=180°∴∠A=60°∴∠B=120°∴∠C=∠A=60° ∠D=∠B=60°2、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?ABCD解:四边形ABCD是平行四边形新知应用小结:平行四边形两邻边的和等于周长的一半。§18.1 .1
平行四边形
性质(2)平行四边形有哪些性质?1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心是对角线的交点。
5、周长=两邻边之和×2
6、面积=底边×底边上的高
概念应用
如图: ABCD中,EF∥AB
若GH∥AD,EF与GH交于点O,
则图中有__个平行四边形。
ABDCEFGH9O选择:平行四边形具有而一般四边形不具有 的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度B例1:如图,在 ABCD中ABCD1.基础知识:若∠A=130 ° ,则∠B=______ 、∠C=______ 、∠D=______2.变式训练: a、若∠A+ ∠C= 200 ° ,则∠A=______ 、 ∠B=______
b、若∠A:∠B= 5:4,则∠C=______ 、∠D=______50 °130 °50 °100 °80 °100 °80 °EF3.拓展延伸:若AE、AF为BC、CD边上的高,且∠EAF=60°则∠C = ——
∠B=——.
120 °60 °例2 如图1 ABCD中AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____441例3 如图2 , ABC,AB=AC=10,则 ADEF的周长为_____ABCDEF20例4 如图3 ABCD中,BC=5,AC=4,∠BAC=90.则 ABCD 的面积为 _____ABCD12图1图2图31、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .又若AB=13厘米,则△COD的周长为 。(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。2.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 209cm12cm34cm36cmD练一练练一练3、有没有这样的平行四边形,它的两条对角线长分别为14cm和20cm,它的一边长为18cm?为什么?若平行四边形的一边长为xcm,则x的取值范围为多少?3cm<x<17cm练一练4、已知O是 ABCD两条对角线的交点,若已知AB=5,△OAB的周长比△OBC的周长短3,则BC=____ 82cm或8cm ABCD的周长为44cm, 对角线AC、BD相交于
O, 且△AOD的周长比△AOB的周长少2cm,
求 ABCD各边的长.
6、已知如图,在 ABCD中, E、F分别是边BC和AD上的点,且BE=DF。求证:①△ABE≌△CDF
②AE=CFABCDEF小结:运用平行四边形的性质可证明线段、角相等或三角形全等。新知应用7、已知如下图,在 ABCD中,AC与BD相交于点O,点E、F在AC上,且BE∥DF。
求证:BE=DFABCDOEF证明:∵BE∥DF
∴∠BEO=∠DFO( )
∵四边形ABCD是平行四边形
∴OB=OD ( )
又∠BOE=∠DOF
∴⊿BOE≌⊿DOF ( )
∴BE=DF ( )两直线平行,内错角相等平行四边形的对角线互相平分SAS全等三角形的对应边相等5、已知 ABCD中,AE⊥BD, AF⊥BD,垂足为E、F,
求证:EB=DFABCDEF ABCD中,∠A=150°,AB=8cm,BC=10cm,
求:四边形ABCD的面积ABCDE解:过点A作AE ⊥ BC交BC于E。
∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠BAD+∠B=180°
∵ ∠BAD=150 ° ∴∠B=30 °
在Rt⊿ABE中,∠B=30 °
∴AE= AB=4, ∴ S ABCD=4×10=40(cm)试一试如图,已知平行四边形ABCD,以一组对边AD、BC向形外作等边△ADE和等边△ BCF,连结BE、DF,探索BE、DF的大小关系。挑战自我 已知平面上任意三点A、B、C,是否存在一点D,使A、B、C、D四点围成一个平行四边形。若存在,请你作出图形;若不存在,请说明理由。2018年12月16日星期日39如图,在平面直角坐标系中, OBCD的顶点
O﹑B﹑D的坐标如图所示,则顶点C的
坐标为( )xYCO (0,0)B(5,0)D(2,3)A. (3,7) B. (5,3)
C. (7,3) D. (8,2)C§18.1 .1
平行四边形
性质(3)平行四边形有哪些性质?1、边:对边平行且相等;
2、角:对角相等, 邻角互补;
3、对角线:对角线互相平分;
4、对称性:是中心对称图形,对称中心是对角线的交点。
5、周长=两邻边之和×2
6、面积=底边×底边上的高
选择题:
1、 ABCD中,∠A比∠B大20°则∠C的度数( )
A、60 ° B、80 ° C、100° D、120°
2、 ABCD的周长为40cm,⊿ABC的周长为25cm,则对角 线AC长为 ( )
A、5cm B、 15cm C、 6cm D、 16cm
3、 ABCD中, ∠ A=43 ° ,过点A作BC和CD的垂线,那么这两条垂线的夹角度数为 ( )
A、113° B、115 ° C、137° D、90°CAC如图,在 ABCD中,BE平分∠ABC交AD于E,BC=8㎝,CD=6㎝, ∠D=60°,则下列说法中错误的是( )
∠C=120° B. AE=6 ㎝
C. AD=8 ㎝ D. ∠BED=140 °ABCDED6860°66 1.夹在两条平行线间的平行线段相等.
2.两条平行线间的距离处处相等.ABA′B′AB、A‘B’:夹在两条平行线间的平行线段.
CD、C‘D’:夹在两条平行线间的垂线段.CDC′D′两条平行线间的距离:两条平行线中,一条平行线上的点到另一条直线的距离,叫做两条平行线之间的距离。练一练:利用面积相等求两平行线间的距离10解:∵ AC⊥BC∴BC2=AB2-AC2=25=16=9(勾股定理)∴ BC=3∵ 四边形ABCD是平行四边形∴CE= AC=2,BD=2BE∴∴BD=2BE=(平行四边形对角线互相平分)(勾股定理)你还有别的方法吗?(1)△ABE的面积为 ______cm226练一练:4利用三角形面积求两平行线间的距离(2)若AB=4cm,则AB和DE间的
距离为 _____cm2 如图,E是直线CD上的一点。已知平行四边形ABCD的面积为52cm2,134如图, □ ABCD的两条对角线相交于点O.
(1)图中有多少对全等三角形?
请把它们写出来;
(2)图中有多少对面积相等的
三角形? 有一块平行四边形的草地,学校想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?想一想有无数种分法,分割线只要过对角线的交点 ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F.
求证:OE=OF巩固新知请判断下列图中,OE=OF还成立么? 过对角线交点的任一条直线都将平行四边形分成面积相等的两部分。4、一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗? O练一练MADBNQCP1﹑已知:如下图 ABCD中,平行于对角线AC的直线MN分别交DA﹑ DC的延长线于点M﹑N,交BA﹑BC于点P、Q,求证:MQ=NP
