5.1任意角和弧度制 同步练习(含解析)
文档属性
| 名称 | 5.1任意角和弧度制 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 730.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 00:00:00 | ||
图片预览




文档简介
5.1任意角和弧度制同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知角终边上有一点,则为( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
2.下列命题中,正确的是( )
A.1弧度的角就是长为半径的弦所对的圆心角
B.若是第一象限的角,则也是第一象限的角
C.若两个角的终边重合,则这两个角相等
D.用角度制和弧度制度量角,都与圆的半径有关
3.下列各角中,与角终边重合的是( )
A. B. C. D.
4.砖雕是我国古建筑雕刻中的重要艺术形式,传统砖雕精致细腻、气韵生动、极富书卷气.如图所示,一扇环形砖雕,可视为将扇形OCD截去同心扇形OAB所得图形,已知,,,则该扇环形砖雕的面积为( ).
A. B. C. D.
5.在半径为9的圆中,的圆心角所对弧长为( )
A.900 B. C. D.
6.已知扇形的周长为8cm,面积是,则扇形的圆心角的弧度数是( )
A. B.1 C.2 D.3
7.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为1cm)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁以的速度爬行,黑蚂蚁以的速度爬行,则2秒钟后,两只蚂蚁之间的直线距离为( )
A.1 B. C. D.
8.设r为圆的半径,弧长为的圆弧所对的圆心角为( )
A. B. C. D.
二、多选题
9.下列说法正确的有( )
A.终边在轴上的角的集合为
B.已知,则
C.已知幂函数的图象过点,则
D.已知,且,则的最小值为8
10.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B.
C. D.
11.下列各说法,正确的是( )
A.半圆所对的圆心角是π rad
B.圆周角的大小等于2π
C.1 弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1 弧度
12.若角的终边与角的终边关于轴对称,且,则的值可能为( )
A. B. C. D.
三、填空题
13.如图1,折扇又名“撒扇”“纸扇”,是一种用竹木或象牙做扇骨, 纸或绫绢做扇面的能折叠的扇子,其展开的平面图如图2的扇形,其中,则扇面(曲边四边形)的面积是 .
14.如图,在△ABC中,BC=4,以点A为圆心,2为半径⊙A的与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是 .(结果保留π)
15.若角的终边与角的终边相同,则在内与角的终边相同的角是 .
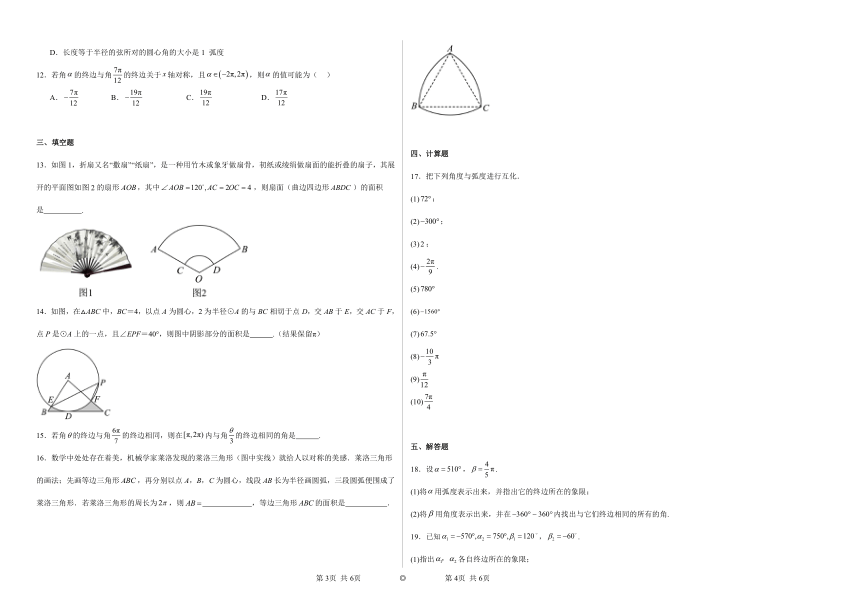
16.数学中处处存在着美,机械学家莱洛发现的莱洛三角形(图中实线)就给人以对称的美感.莱洛三角形的画法;先画等边三角形,再分别以点A,B,C为圆心,线段长为半径画圆弧,三段圆弧便围成了莱洛三角形.若莱洛三角形的周长为,则 ,等边三角形的面积是 .
四、计算题
17.把下列角度与弧度进行互化.
(1);
(2);
(3);
(4).
(5)
(6)
(7)
(8)
(9)
(10)
五、解答题
18.设,.
(1)将用弧度表示出来,并指出它的终边所在的象限;
(2)将用角度表示出来,并在内找出与它们终边相同的所有的角.
19.已知,.
(1)指出各自终边所在的象限;
(2)在内找出与终边相同的所有角.
20.如图,圆的半径为5,弦的长为 5.
(1)求圆心角的大小;
(2)求扇形的弧长及阴影部分的面积.
21.如图,点A,B,C是圆上的点.
(1)若,,求扇形AOB的面积和弧AB的长;
(2)若扇形AOB的面积为,求扇形AOB周长的最小值,并求出此时的值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】根据角终边上的点所在象限判断即可.
【详解】因为点在第四象限,
所以角为第四象限角.
故选:D.
2.B
【分析】由角度制和弧度制的定义,象限角的概念,判断各选项的正误.
【详解】1弧度的角就是长为半径的弧所对的圆心角,A选项错误;
若是第一象限的角,则是第四象限的角,所以是第一象限的角,B选项正确;
当,时,与终边重合,但两个角不相等,C选项错误;
不论是用角度制还是弧度制度量角,由角度值和弧度值的定义可知度量角与所取圆的半径无关,D选项错误.
故选:B
3.C
【分析】根据角的终边相同的集合判断选择即可.
【详解】与角终边重合的角为:,则当时,,故C正确.
经检验,其他选项都不正确.
故选:C.
4.D
【分析】根据题意,利用扇形的面积公式,即可求得扇环的面积,得到答案.
【详解】由题意知,,,,可得,
可得扇形的面积为,扇形的面积为,
所以该扇环形砖雕的面积为.
故选:D.
5.B
【分析】根据角度制与弧度制转化并结合弧长公式即可得到答案.
【详解】,则所对弧长为.
故选:B
6.C
【分析】根据扇形的面积公式及弧长公式,即可求得.
【详解】设扇形的弧长为,半径为,所以,,则,
所以扇形的圆心角的弧度数是.
故选:C.
7.A
【分析】作图利用单位圆解几何图形即可.
【详解】
如图所示,红蚂蚁以的速度爬行,黑蚂蚁以的速度爬行,
则2秒钟后,红蚂蚁绕圆的角度为,到达B处,黑蚂蚁绕圆的角度为,到达C处,
此时,即为正三角形,故.
故选:A
8.A
【分析】根据弧长、圆心角、半径的关系,代入求解,再转化为角度制即可.
【详解】由弧长、圆心角、半径的关系:,
弧长为的圆弧所对的圆心角:.
故选:A.
9.BC
【分析】A选项,终边在轴上的角的集合为;B选项,将指数式化为对数式,根据对数运算性质得到;C选项,根据函数为幂函数得到,再代入,求出,得到答案;D选项,根据基本不等式“1”的妙用求出最小值.
【详解】A选项,终边在轴上的角的集合为,A错误;
B选项,因为,所以,
故,B正确;
C选项,因为为幂函数,所以,
故,将代入得到,解得,
故,C正确;
D选项,因为,
所以,
当且仅当,即时,等号成立,
故的最小值为9,D错误.
故选:BC
10.BC
【分析】根据各集合所表示的角的范围一一分析即可.
【详解】对于A选项,除了锐角,还包括其它角,比如,所以A选项错误.
对于B选项,锐角是小于的角,故B选项正确.
对于C选项,锐角是第一象限角,故C选项正确.
对于D选项,中角的范围不一样,所以D选项错误.
故选:BC.
11.ABC
【分析】根据弧度制的定义即可判断.
【详解】由弧度制的定义可知:长度等于半径的弧所对的圆心角的大小是1弧度,则长度等于半径的弦所对的圆心角的大小不是1弧度,D的说法错误,
根据弧度的定义及角度与弧度的换算可知,ABC的说法正确.
故选:ABC
12.AD
【分析】写出,,再根据其范围即可得到答案.
【详解】因为角的终边与角的终边关于x轴对称,
所以,,
又因为,所以当时,,
当时,.
故选:AD.
13./
【分析】由大扇形面积减去小扇形面积即可得.
【详解】,
由题意可得,扇形的面积是,扇形的面积是.则扇面(曲边四边形)的面积是.
故答案为:.
14.
【分析】根据条件得到,从而由扇形的面积公式求得扇形的面积,再求出的面积,即可求解.
【详解】由,
则,即,
又,则扇形的面积为,
又BC=4,⊙A与BC相切于点D,
所以,
即图中阴影部分的面积是,
故答案为:.
15./
【分析】根据终边相同角的表示,求得,令,求得,进而得到答案.
【详解】因为角θ的终边与角的终边相同,可得,
所以,
令,解得,所以,
所以在内与角的终边相同的角为.
故答案为:.
16.
【分析】根据条件,利用弧长公式即可求出,再利用三角形的面积公式求出三角形的面积即可.
【详解】由条件可知,弧长,
由,得三角形的边长.
在等边三角形中,边上的高为,
所以等边三角形的面积是.
故答案为:;.
17.(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
【分析】(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)由弧度制和角度值的转化公式解即可得出答案.
【详解】(1).
(2).
(3).
(4).
(5).
(6).
(7).
(8).
(9)
(10).
18.(1),第二象限
(2);,
【分析】(1)利用将角度化为弧度,并得到其所在象限;
(2)利用将弧度化为角度,并写出与终边相同角的表示,根据范围列不等式即可求解.
【详解】(1)因为,所以,
所以的终边在第二象限;
(2),设,
因为,所以,所以或,
所以在内与终边相同的角是,.
19.(1) 在第二象限; 第一象限
(2)与终边相同的所有角有,与终边相同的角为.
【分析】(1)(2)根据终边相同的角即可求解.
【详解】(1),在第二象限;
在第一象限;
(2),与终边相同的角为,取
范围内与它们终边相同的所有角有
与终边相同的角为,取,
则范围内与它们终边相同的所有角有.
20.(1)
(2),
【分析】(1)由等边三角形即可求解角.
(2)利用弧长公式以及扇形的面积公式即可求解.
【详解】(1)由于圆O的半径为,弦AB的长为5,所以为等边三角形,所以.
(2)因为,所以,,又,所以阴影部分的面积
21.(1)面积为,弧AB的长为
(2),
【分析】(1)根据扇形的弧长公式和面积公式进行计算即可.(2)根据扇形的弧长公式和面积公式结合基本不等式的应用进行求解.
【详解】(1)由题意知,设,所以
根据扇形弧长;
扇形面积;
(2)由,即,
扇形的周长为当且仅当等号成立,
所以由知:.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知角终边上有一点,则为( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
2.下列命题中,正确的是( )
A.1弧度的角就是长为半径的弦所对的圆心角
B.若是第一象限的角,则也是第一象限的角
C.若两个角的终边重合,则这两个角相等
D.用角度制和弧度制度量角,都与圆的半径有关
3.下列各角中,与角终边重合的是( )
A. B. C. D.
4.砖雕是我国古建筑雕刻中的重要艺术形式,传统砖雕精致细腻、气韵生动、极富书卷气.如图所示,一扇环形砖雕,可视为将扇形OCD截去同心扇形OAB所得图形,已知,,,则该扇环形砖雕的面积为( ).
A. B. C. D.
5.在半径为9的圆中,的圆心角所对弧长为( )
A.900 B. C. D.
6.已知扇形的周长为8cm,面积是,则扇形的圆心角的弧度数是( )
A. B.1 C.2 D.3
7.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为1cm)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁以的速度爬行,黑蚂蚁以的速度爬行,则2秒钟后,两只蚂蚁之间的直线距离为( )
A.1 B. C. D.
8.设r为圆的半径,弧长为的圆弧所对的圆心角为( )
A. B. C. D.
二、多选题
9.下列说法正确的有( )
A.终边在轴上的角的集合为
B.已知,则
C.已知幂函数的图象过点,则
D.已知,且,则的最小值为8
10.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B.
C. D.
11.下列各说法,正确的是( )
A.半圆所对的圆心角是π rad
B.圆周角的大小等于2π
C.1 弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1 弧度
12.若角的终边与角的终边关于轴对称,且,则的值可能为( )
A. B. C. D.
三、填空题
13.如图1,折扇又名“撒扇”“纸扇”,是一种用竹木或象牙做扇骨, 纸或绫绢做扇面的能折叠的扇子,其展开的平面图如图2的扇形,其中,则扇面(曲边四边形)的面积是 .
14.如图,在△ABC中,BC=4,以点A为圆心,2为半径⊙A的与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是 .(结果保留π)
15.若角的终边与角的终边相同,则在内与角的终边相同的角是 .
16.数学中处处存在着美,机械学家莱洛发现的莱洛三角形(图中实线)就给人以对称的美感.莱洛三角形的画法;先画等边三角形,再分别以点A,B,C为圆心,线段长为半径画圆弧,三段圆弧便围成了莱洛三角形.若莱洛三角形的周长为,则 ,等边三角形的面积是 .
四、计算题
17.把下列角度与弧度进行互化.
(1);
(2);
(3);
(4).
(5)
(6)
(7)
(8)
(9)
(10)
五、解答题
18.设,.
(1)将用弧度表示出来,并指出它的终边所在的象限;
(2)将用角度表示出来,并在内找出与它们终边相同的所有的角.
19.已知,.
(1)指出各自终边所在的象限;
(2)在内找出与终边相同的所有角.
20.如图,圆的半径为5,弦的长为 5.
(1)求圆心角的大小;
(2)求扇形的弧长及阴影部分的面积.
21.如图,点A,B,C是圆上的点.
(1)若,,求扇形AOB的面积和弧AB的长;
(2)若扇形AOB的面积为,求扇形AOB周长的最小值,并求出此时的值.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
【分析】根据角终边上的点所在象限判断即可.
【详解】因为点在第四象限,
所以角为第四象限角.
故选:D.
2.B
【分析】由角度制和弧度制的定义,象限角的概念,判断各选项的正误.
【详解】1弧度的角就是长为半径的弧所对的圆心角,A选项错误;
若是第一象限的角,则是第四象限的角,所以是第一象限的角,B选项正确;
当,时,与终边重合,但两个角不相等,C选项错误;
不论是用角度制还是弧度制度量角,由角度值和弧度值的定义可知度量角与所取圆的半径无关,D选项错误.
故选:B
3.C
【分析】根据角的终边相同的集合判断选择即可.
【详解】与角终边重合的角为:,则当时,,故C正确.
经检验,其他选项都不正确.
故选:C.
4.D
【分析】根据题意,利用扇形的面积公式,即可求得扇环的面积,得到答案.
【详解】由题意知,,,,可得,
可得扇形的面积为,扇形的面积为,
所以该扇环形砖雕的面积为.
故选:D.
5.B
【分析】根据角度制与弧度制转化并结合弧长公式即可得到答案.
【详解】,则所对弧长为.
故选:B
6.C
【分析】根据扇形的面积公式及弧长公式,即可求得.
【详解】设扇形的弧长为,半径为,所以,,则,
所以扇形的圆心角的弧度数是.
故选:C.
7.A
【分析】作图利用单位圆解几何图形即可.
【详解】
如图所示,红蚂蚁以的速度爬行,黑蚂蚁以的速度爬行,
则2秒钟后,红蚂蚁绕圆的角度为,到达B处,黑蚂蚁绕圆的角度为,到达C处,
此时,即为正三角形,故.
故选:A
8.A
【分析】根据弧长、圆心角、半径的关系,代入求解,再转化为角度制即可.
【详解】由弧长、圆心角、半径的关系:,
弧长为的圆弧所对的圆心角:.
故选:A.
9.BC
【分析】A选项,终边在轴上的角的集合为;B选项,将指数式化为对数式,根据对数运算性质得到;C选项,根据函数为幂函数得到,再代入,求出,得到答案;D选项,根据基本不等式“1”的妙用求出最小值.
【详解】A选项,终边在轴上的角的集合为,A错误;
B选项,因为,所以,
故,B正确;
C选项,因为为幂函数,所以,
故,将代入得到,解得,
故,C正确;
D选项,因为,
所以,
当且仅当,即时,等号成立,
故的最小值为9,D错误.
故选:BC
10.BC
【分析】根据各集合所表示的角的范围一一分析即可.
【详解】对于A选项,除了锐角,还包括其它角,比如,所以A选项错误.
对于B选项,锐角是小于的角,故B选项正确.
对于C选项,锐角是第一象限角,故C选项正确.
对于D选项,中角的范围不一样,所以D选项错误.
故选:BC.
11.ABC
【分析】根据弧度制的定义即可判断.
【详解】由弧度制的定义可知:长度等于半径的弧所对的圆心角的大小是1弧度,则长度等于半径的弦所对的圆心角的大小不是1弧度,D的说法错误,
根据弧度的定义及角度与弧度的换算可知,ABC的说法正确.
故选:ABC
12.AD
【分析】写出,,再根据其范围即可得到答案.
【详解】因为角的终边与角的终边关于x轴对称,
所以,,
又因为,所以当时,,
当时,.
故选:AD.
13./
【分析】由大扇形面积减去小扇形面积即可得.
【详解】,
由题意可得,扇形的面积是,扇形的面积是.则扇面(曲边四边形)的面积是.
故答案为:.
14.
【分析】根据条件得到,从而由扇形的面积公式求得扇形的面积,再求出的面积,即可求解.
【详解】由,
则,即,
又,则扇形的面积为,
又BC=4,⊙A与BC相切于点D,
所以,
即图中阴影部分的面积是,
故答案为:.
15./
【分析】根据终边相同角的表示,求得,令,求得,进而得到答案.
【详解】因为角θ的终边与角的终边相同,可得,
所以,
令,解得,所以,
所以在内与角的终边相同的角为.
故答案为:.
16.
【分析】根据条件,利用弧长公式即可求出,再利用三角形的面积公式求出三角形的面积即可.
【详解】由条件可知,弧长,
由,得三角形的边长.
在等边三角形中,边上的高为,
所以等边三角形的面积是.
故答案为:;.
17.(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
【分析】(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)由弧度制和角度值的转化公式解即可得出答案.
【详解】(1).
(2).
(3).
(4).
(5).
(6).
(7).
(8).
(9)
(10).
18.(1),第二象限
(2);,
【分析】(1)利用将角度化为弧度,并得到其所在象限;
(2)利用将弧度化为角度,并写出与终边相同角的表示,根据范围列不等式即可求解.
【详解】(1)因为,所以,
所以的终边在第二象限;
(2),设,
因为,所以,所以或,
所以在内与终边相同的角是,.
19.(1) 在第二象限; 第一象限
(2)与终边相同的所有角有,与终边相同的角为.
【分析】(1)(2)根据终边相同的角即可求解.
【详解】(1),在第二象限;
在第一象限;
(2),与终边相同的角为,取
范围内与它们终边相同的所有角有
与终边相同的角为,取,
则范围内与它们终边相同的所有角有.
20.(1)
(2),
【分析】(1)由等边三角形即可求解角.
(2)利用弧长公式以及扇形的面积公式即可求解.
【详解】(1)由于圆O的半径为,弦AB的长为5,所以为等边三角形,所以.
(2)因为,所以,,又,所以阴影部分的面积
21.(1)面积为,弧AB的长为
(2),
【分析】(1)根据扇形的弧长公式和面积公式进行计算即可.(2)根据扇形的弧长公式和面积公式结合基本不等式的应用进行求解.
【详解】(1)由题意知,设,所以
根据扇形弧长;
扇形面积;
(2)由,即,
扇形的周长为当且仅当等号成立,
所以由知:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
