数学人教A版(2019)必修第一册3.2.2奇偶性 课件(共46张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.2奇偶性 课件(共46张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 16:04:37 | ||
图片预览








文档简介
(共46张PPT)
3.2.2 奇偶性
第三章 函数概念与性质
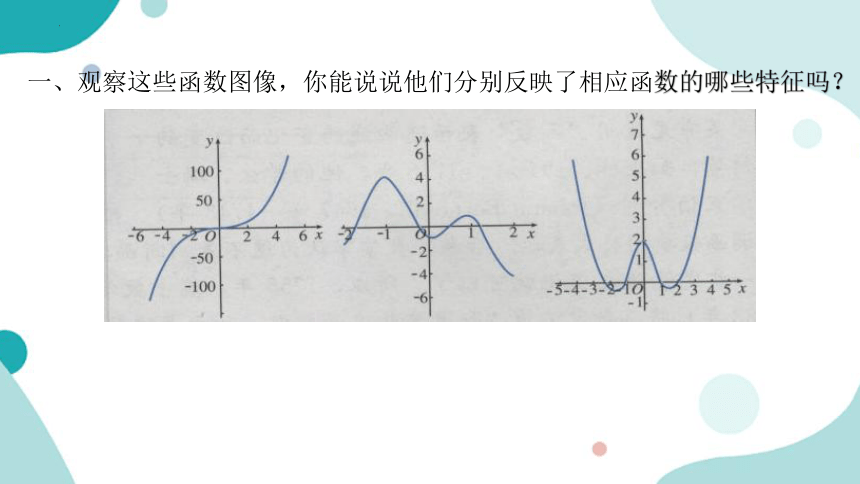
一、观察这些函数图像,你能说说他们分别反映了相应函数的哪些特征吗?
新课
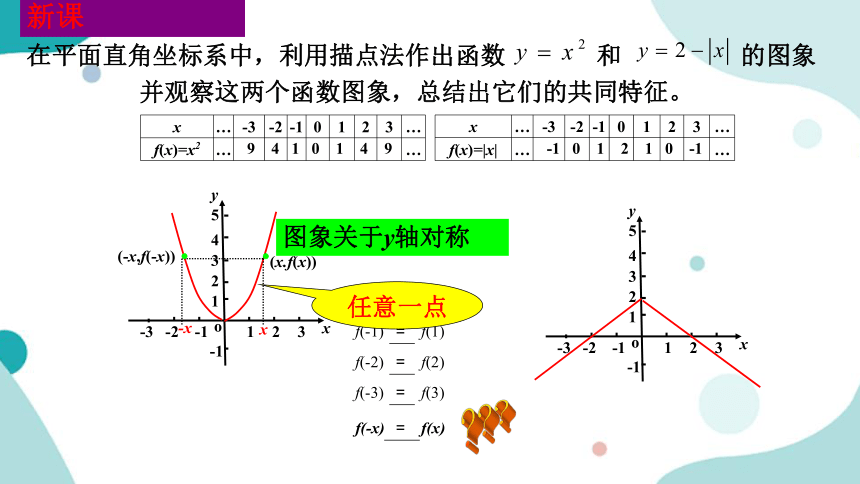
在平面直角坐标系中,利用描点法作出函数 和 的图象
并观察这两个函数图象,总结出它们的共同特征。
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
x … -3 -2 -1 0 1 2 3 …
f(x)=x2 … …
9 4 1 0 1 4 9
x … -3 -2 -1 0 1 2 3 …
f(x)=|x| … …
-1 0 1 2 1 0 -1
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
图象关于y轴对称
f(-1)
f(1)
f(-2)
f(2)
f(-3)
f(3)
=
=
=
-x
x
(x.f(x))
(-x,f(-x))
f(-x)
f(x)
=
任意一点
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x), 那么函数f(x) 就叫做偶函数.
偶函数
偶函数的图象关于y轴对称.
偶函数的定义域关于原点对称.
O
a
-a
b
-b
思考:定义中“任意一个x,都有f(-x)=f(x)成立”说明了什么?
f(-x)与f(x)都有意义,
说明-x、x必须同时属于定义域,
判断下列函数是否为偶函数。
是
不是
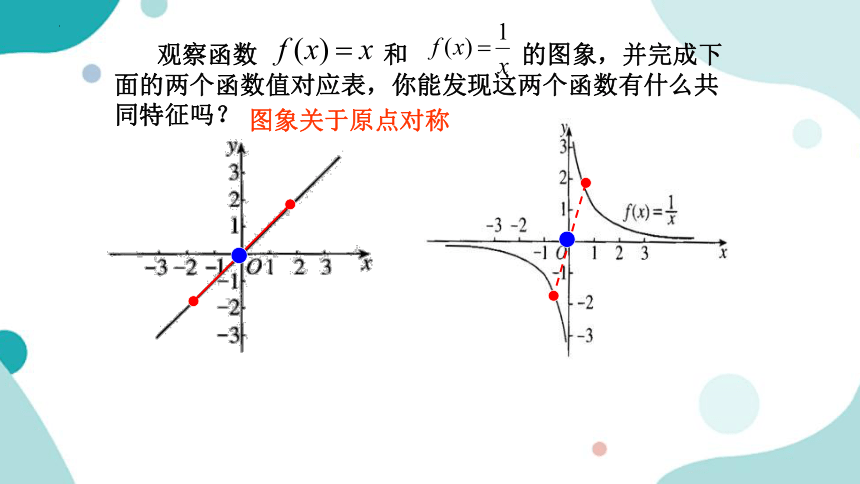
观察函数 和 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
图象关于原点对称
x
-x
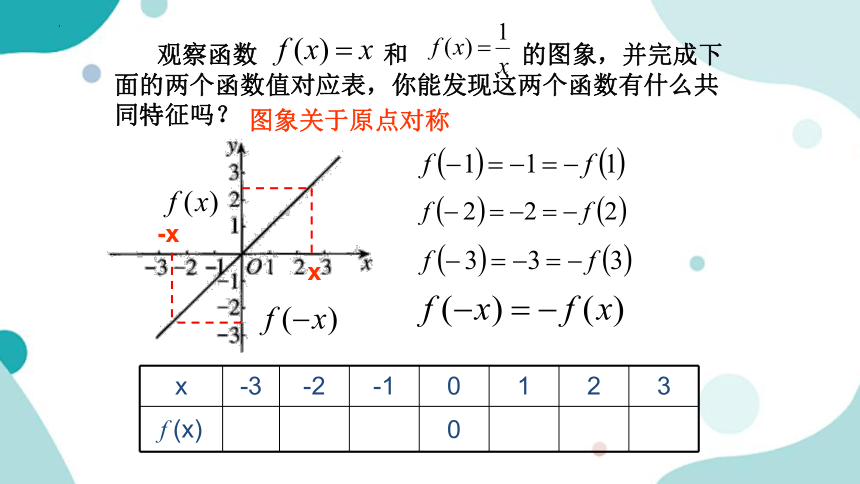
观察函数 和 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
x -3 -2 -1 0 1 2 3
f (x) -3 -2 -1 0 1 2 3
图象关于原点对称
奇函数的定义:
奇函数要满足:
①、定义域关于原点对称
奇函数图象特征:
奇函数的图象关于原点对称,反之,一个函数的图象关于原点对称,那么它是奇函数.
一般地,如果对于函数f(x)的定义域内任意一个x,都有 ,那么函数f(x)就叫做奇函数.
②
已知函数f(x)是奇函数,定义域为D,若0∈D,f(0)是否为定值
∵f(x)为奇函数,∴对任意x∈D,f(-x)=-f(x),∴f(-0)=-f(0),即f(0)=0,为定值.
达标检测
例1:判断下列函数的奇偶性:
解:(1)函数f(x)=x4的定义域是R.因为对于任意的x∈R,都有
f(-x)=(x)4 =x4= f(x),
所以函数f(x)=x4是偶函数。
(2)函数f(x)= x3的定义域是R.因为对于任意的x∈R,都有
f(-x)= (-x)3 = -x3 = -f(x),
所以函数f(x)= x3是奇函数。
例1:判断下列函数的奇偶性:
解:(3)函数 的定义域是 .因为对于任意的 ,都有 ,
所以函数 是奇函数。
(4)函数 的定义域是 .因为对于任意的 ,都有 ,
所以函数 是奇函数。
1.定义法判断函数的奇偶性要“二看”
(1)一看定义域.定义域A要关于原点对称,即对任意x∈A,-x∈A,定义域不关于原点对称时,f(x)既不是奇函数,也不是偶函数.
如f(x)=x2,x∈R是偶函数,但f(x)=x2,x∈[-1,2]既不是奇函数,也不是偶函数.
(2)二看等式.当f(x)的定义域关于原点对称时,要看f(x)与f(-x)的关系:
①f(-x)=f(x) f(x)是偶函数;
②f(-x)=-f(x) f(x)是奇函数;
③f(-x)≠±f(x) f(x)既不是奇函数,也不是偶函数;
④f(-x)=±f(x) f(x)既是奇函数又是偶函数.这样的函数只有一类,即f(x)=0,x∈D,且D关于原点对称.
根据定义判断函数的奇偶性的步骤:
(3)、根据定义下结论.
判断函数的奇偶性的方法:
(1)、先求定义域,看是否关于原点对称;
(2)、再判断f (-x)=-f (x)或f (-x)=f (x)是否恒成立;
图象法、定义法
思考:(1)判断函数 的奇偶性。
(2)如图,是函数 图象的一部分,
你能根据函数的奇偶性 画出它在y轴左边的图象吗?
(3)一般地,如果知道函数为偶(奇)函数,那么
我们可以怎样简化对它的研究?
(1)奇函数
根据它的图象关于坐标原点对称或关于y轴对称的性质,只要把这个函数的定义域分成关于坐标原点对称的两部分,由函数在其中一部分上的图象和性质,即可推断出它在整个定义域内的图象和性质
微判断
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若f(x)的定义域关于原点对称,则f(x)是偶函数.( )
(2)若f(x)是偶函数,则它的定义域关于原点对称.( )
(3)若f(-2)=f(2),则f(x)(x∈R)是偶函数.( )
(4)若f(x)(x∈R)是偶函数,则f(-2)=f(2).( )
(5)若f(2)≠f(-2),则f(x)(x∈R)不是偶函数.( )
(6)既是奇函数又是偶函数的函数一定是f(x)=0(x∈R).( )
答案: (1)× (2)√ (3)× (4)√ (5)√ (6)×
解析:只有f(x)的定义域关于原点对称,且f(-x)=f(x)时,f(x)才是偶函数,故(1)错误;
f(x)的定义域关于原点对称是f(x)为偶函数的必要条件,故(2)正确;
对任意x∈R,满足f(-x)=f(x),f(x)才是偶函数,仅凭两个特殊的函数值相等不足以判断函数的奇偶性,故(3)错误而(4)正确;
为了说明f(x)不是偶函数,举一个反例即可,故(5)正确;
f(x)=0,定义域为[-1,1],该函数既是奇函数又是偶函数,故(6)错误.
例1判断下列函数的奇偶性:
分析利用奇函数、偶函数的定义判断函数的奇偶性时,先求出函数的定义域,看其是否关于原点对称,如果定义域关于原点对称,再判断f(-x)与f(x)的关系.为了判断f(-x)与f(x)的关系,既可以从f(-x)开始化简整理,也可以考虑f(-x)+f(x)或f(-x)-f(x)是否等于0.当f(x)不等于0时也可考虑 与1或-1的关系,还可以考虑使用图象法.
一、判断函数的奇偶性
解:(1)函数的定义域为{x|x≠-1},不关于原点对称,故f(x)既不是奇函数又不是偶函数.
(2)函数的定义域为R,关于原点对称,f(-x)=(-x)3-2(-x)=2x-x3=-f(x),∴f(x)是奇函数.
函数的定义域为{-1,1},关于原点对称.
又f(1)=f(-1)=0,故f(x)既是奇函数又是偶函数.
(4)函数的定义域关于原点对称.
(方法一)当x>0时,-x<0,
f(-x)=-x[1-(-x)]=-x(1+x)=-f(x).
当x<0时,-x>0,f(-x)=(-x)[1+(-x)]=-x(1-x)=-f(x).∴f(-x)=-f(x).
∴f(x)是奇函数.
图象关于原点对称,∴f(x)是奇函数.
1.根据奇偶性可将函数分为奇函数,偶函数,既是奇函数也是偶函数,既不是奇函数又不是偶函数.
2.判断函数奇偶性的两种方法
(1)定义法:
(2)图象法:
变式训练判断下列函数的奇偶性:
(2)f(x)=|x+2|+|x-2|;
(3)f(x)=0.
(2)f(x)的定义域是R,又f(-x)=|-x+2|+|-x-2|=|x-2|+|x+2|=f(x),所以f(x)是偶函数.
(3)因为f(x)的定义域为R,又f(-x)=0=f(x),且f(-x)=0=-f(x),所以f(x)既是奇函数又是偶函数.
二、奇、偶函数的运算性质及复合函数的奇偶性
设非零函数f(x),g(x)的定义域分别是F,G,若F=G,则有下列结论:
注意:上述表格中不考虑f(x)±g(x)=0;f[g(x)]中,需x∈G,g(x)∈F.
内偶则偶,内奇同外
偶()偶得偶,奇()奇得奇
同偶异奇
例 已知定义域R上的奇函数,定义在R上偶函数,则下列函数中是奇函数的有( )
C
三、函数奇偶性与单调性的关系
1.奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性.上述结论可简记为“奇同偶异”.
2.偶函数在关于原点对称的区间上有相同的最大(小)值,取得最值时的自变量的值互为相反数;奇函数在关于原点对称的区间上取得的最值互为相反数,取得最值时的自变量的值也互为相反数.
微练习
若奇函数f(x)在[-6,-2]上是减函数,且最小值是1,则它在[2,6]上是( )
A.增函数且最小值是-1
B.增函数且最大值是-1
C.减函数且最大值是-1
D.减函数且最小值是-1
答案:C
解析:∵奇函数f(x)在[-6,-2]上是减函数,且最小值是1,∴函数f(x)在[2,6]上是减函数且最大值是-1.
2.设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=( )
A.-1 B.-3 C.1 D.3
答案:B
解析:当x≤0时,f(x)=2x2-x,f(-1)=2×(-1)2-(-1)=3.因为f(x)是定义在R上的奇函数,
故f(1)=-f(-1)=-3,故选B.
1.比较函数值的大小
例3已知偶函数f(x)的定义域为R,当f(x)在区间[0,+∞)上单调递增,则f(-2),f(π),f(-3)的大小关系是( )
A.f(π)>f(-3)>f(-2)
B.f(π)>f(-2)>f(-3)
C.f(π)D.f(π)答案:A
解析:∵f(x)在R上是偶函数,∴f(-2)=f(2),f(-3)=f(3).∵2<3<π,且f(x)在区间[0,+∞)上单调递增,
∴f(2)函数奇偶性与单调性的综合应用
注意:先利用函数的奇偶性将自变量转化到同一个单调区间上,再根据函数的单调性对函数值的大小作出比较.
延伸探究(1)若将本例中的“增函数”改为“减函数”,其他条件不变,则f(-2),f(π),f(-3)的大小关系如何
(2)若将本例中的“偶函数”改为“奇函数”,其他条件不变,比较这三个函数值的大小.
解:(1)因为当x∈[0,+∞)时,f(x)是减函数,所以有f(2)>f(3)>f(π).又因为f(x)是R上的偶函数,所以f(-2)=f(2),f(-3)=f(3),
从而有f(-2)>f(-3)>f(π).
(2)因为函数为定义在R上的奇函数,且在[0,+∞)上单调递增,所以函数在R上是增函数,
因为-3<-2<π,所以f(-3)2.解函数不等式
例4已知定义在区间[-2,2]上的奇函数f(x)在区间[0,2]上单调递增,若f(1-m)解:因为f(x)在区间[-2,2]上为奇函数,且在区间[0,2]上单调递减,所以f(x)在[-2,2]上单调递减.
反思感悟解有关奇函数f(x)的不等式f(a)+f(b)<0,先将f(a)+f(b)<0变形为f(a)<-f(b)=f(-b),再利用f(x)的单调性去掉“f”,化为关于a,b的不等式.另外,要特别注意函数的定义域.
由于偶函数在关于原点对称的两个区间上的单调性相反,所以我们要利用偶函数的性质f(x)=f(|x|)=f(-|x|)将f(g(x))中的g(x)全部化到同一个单调区间内,再利用单调性去掉符号f,使不等式得解.
延伸探究若将本例中的“奇函数”改为“偶函数”,把区间“[0,2]”改为“[-2,0]”,其他条件不变,求实数m的取值范围.
解:因为函数为[-2,2]上的偶函数,又函数在[-2,0]上单调递减,所以函数在[0,2]上单调递增,
不等式可化为f(|1-m|)答案:D
3.函数f(x)的定义域为R,且对任意x∈R,有f(x)满足f(-x)=f(x),且f(x)在区间(-∞,-1]上单调递增,则( )
例2已知f(x)为R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(-1);
(2)求f(x)的解析式.
分析(1)根据奇函数的性质,将f(-1)转化为f(1)求解;(2)先设出所求区间上的自变量,利用奇函数、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,再次利用函数的奇偶性求解.注意不要忽略x=0时f(x)的解析式.
四、利用函数的奇偶性求解析式
解:(1)因为函数f(x)为奇函数,
所以f(-1)=-f(1)=-(-2×12+3×1+1)=-2.
(2)当x<0时,-x>0,则
f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.
由于f(x)是奇函数,则f(x)=-f(-x),
所以f(x)=2x2+3x-1.当x=0时,f(-0)=-f(0),则f(0)=-f(0),即f(0)=0.
反思感悟1.这类问题常见的情形是:
已知当x∈(a,b)时,f(x)=φ(x),求当x∈(-b,-a)时f(x)的解析式.
若f(x)为奇函数,则当x∈(-b,-a)时,
f(x)=-f(-x)=-φ(-x);
若f(x)为偶函数,则当x∈(-b,-a)时,
f(x)=f(-x)=φ(-x).
2.若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,不能漏掉.
延伸探究若将本例中的“奇”改为“偶”,“x>0”改为“x≥0”,其他条件不变,求f(x)的解析式.
解:当x<0时,-x>0,此时f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.由于f(x)是偶函数,则f(x)=f(-x)=-2x2-3x+1,所以f(x)的解析式为
五、利用定义法、赋值法解决抽象函数奇偶性问题
典例1若定义在R上的函数f(x)满足:对任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2),且当x>0时,f(x)<0,则( )
A.f(x)是奇函数,且在R上是增函数
B.f(x)是奇函数,且在R上是减函数
C.f(x)是奇函数,且在R上不是单调函数
D.无法确定f(x)的单调性和奇偶性
解析:令x1=x2=0,则f(0)=2f(0),所以f(0)=0.
令x1=x,x2=-x,
则f(-x)+f(x)=f(x-x)=f(0)=0,
所以f(-x)=-f(x),故函数y=f(x)是奇函数.
设x10,所以f(x2-x1)<0,
故f(x2)所以函数y=f(x)在R上是减函数.故选B.
答案:B
典例2已知函数f(x),x∈R,若对于任意实数x1,x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x2),
求证:函数f(x)为偶函数.
证明:令x1=0,x2=x,得f(x)+f(-x)=2f(0)f(x).①
令x2=0,x1=x,得f(x)+f(x)=2f(0)f(x).②
由①②得f(x)+f(-x)=f(x)+f(x),即f(-x)=f(x),所以函数f(x)为偶函数.
反思感悟1.判断抽象函数的奇偶性,应利用函数奇偶性的定义,找准方向,巧妙赋值,合理、灵活变形,找出f(-x)与f(x)的关系,从而判断或证明抽象函数的奇偶性.
2.有时需要在整体上研究f(-x)+f(x)的和的情况.
比如:上面典例1中利用f(-x)+f(x)=0可得出y=f(x)是奇函数.
变式训练定义在R上的函数y=f(x)满足:对任意α,β∈R,总有f(α+β)-[f(α)+f(β)]=2 019,则下列说法正确的是( )
A.f(x)-1是奇函数
B.f(x)+1是奇函数
C.f(x)-2 019是奇函数
D.f(x)+2 019是奇函数
答案:D
解析:令α=β=0,则f(0)-[f(0)+f(0)]=2 019,
即f(0)=-2 019.
令β=-α,则f(0)-[f(α)+f(-α)]=2 019,
即f(α)+f(-α)=-4 038,
则f(-α)+2 019=-2 019-f(α)=-[2 019+f(α)],
即f(x)+2 019是奇函数,故选D.
课堂小结
偶函数 奇函数
定义
图象
定义域
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
关于y轴对称
关于原点对称
关于原点对称
用定义法判断函数的奇偶性的步骤:
①首先确定函数的定义域,并判断其定义域是否关于原点对称;
②确定f(-x)和f(x)的关系;
③作出相应结论。
3.2.2 奇偶性
第三章 函数概念与性质
一、观察这些函数图像,你能说说他们分别反映了相应函数的哪些特征吗?
新课
在平面直角坐标系中,利用描点法作出函数 和 的图象
并观察这两个函数图象,总结出它们的共同特征。
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
x … -3 -2 -1 0 1 2 3 …
f(x)=x2 … …
9 4 1 0 1 4 9
x … -3 -2 -1 0 1 2 3 …
f(x)=|x| … …
-1 0 1 2 1 0 -1
x
y
o
1
2
3
4
5
-1
1
2
3
-1
-2
-3
图象关于y轴对称
f(-1)
f(1)
f(-2)
f(2)
f(-3)
f(3)
=
=
=
-x
x
(x.f(x))
(-x,f(-x))
f(-x)
f(x)
=
任意一点
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x), 那么函数f(x) 就叫做偶函数.
偶函数
偶函数的图象关于y轴对称.
偶函数的定义域关于原点对称.
O
a
-a
b
-b
思考:定义中“任意一个x,都有f(-x)=f(x)成立”说明了什么?
f(-x)与f(x)都有意义,
说明-x、x必须同时属于定义域,
判断下列函数是否为偶函数。
是
不是
观察函数 和 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
图象关于原点对称
x
-x
观察函数 和 的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
x -3 -2 -1 0 1 2 3
f (x) -3 -2 -1 0 1 2 3
图象关于原点对称
奇函数的定义:
奇函数要满足:
①、定义域关于原点对称
奇函数图象特征:
奇函数的图象关于原点对称,反之,一个函数的图象关于原点对称,那么它是奇函数.
一般地,如果对于函数f(x)的定义域内任意一个x,都有 ,那么函数f(x)就叫做奇函数.
②
已知函数f(x)是奇函数,定义域为D,若0∈D,f(0)是否为定值
∵f(x)为奇函数,∴对任意x∈D,f(-x)=-f(x),∴f(-0)=-f(0),即f(0)=0,为定值.
达标检测
例1:判断下列函数的奇偶性:
解:(1)函数f(x)=x4的定义域是R.因为对于任意的x∈R,都有
f(-x)=(x)4 =x4= f(x),
所以函数f(x)=x4是偶函数。
(2)函数f(x)= x3的定义域是R.因为对于任意的x∈R,都有
f(-x)= (-x)3 = -x3 = -f(x),
所以函数f(x)= x3是奇函数。
例1:判断下列函数的奇偶性:
解:(3)函数 的定义域是 .因为对于任意的 ,都有 ,
所以函数 是奇函数。
(4)函数 的定义域是 .因为对于任意的 ,都有 ,
所以函数 是奇函数。
1.定义法判断函数的奇偶性要“二看”
(1)一看定义域.定义域A要关于原点对称,即对任意x∈A,-x∈A,定义域不关于原点对称时,f(x)既不是奇函数,也不是偶函数.
如f(x)=x2,x∈R是偶函数,但f(x)=x2,x∈[-1,2]既不是奇函数,也不是偶函数.
(2)二看等式.当f(x)的定义域关于原点对称时,要看f(x)与f(-x)的关系:
①f(-x)=f(x) f(x)是偶函数;
②f(-x)=-f(x) f(x)是奇函数;
③f(-x)≠±f(x) f(x)既不是奇函数,也不是偶函数;
④f(-x)=±f(x) f(x)既是奇函数又是偶函数.这样的函数只有一类,即f(x)=0,x∈D,且D关于原点对称.
根据定义判断函数的奇偶性的步骤:
(3)、根据定义下结论.
判断函数的奇偶性的方法:
(1)、先求定义域,看是否关于原点对称;
(2)、再判断f (-x)=-f (x)或f (-x)=f (x)是否恒成立;
图象法、定义法
思考:(1)判断函数 的奇偶性。
(2)如图,是函数 图象的一部分,
你能根据函数的奇偶性 画出它在y轴左边的图象吗?
(3)一般地,如果知道函数为偶(奇)函数,那么
我们可以怎样简化对它的研究?
(1)奇函数
根据它的图象关于坐标原点对称或关于y轴对称的性质,只要把这个函数的定义域分成关于坐标原点对称的两部分,由函数在其中一部分上的图象和性质,即可推断出它在整个定义域内的图象和性质
微判断
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若f(x)的定义域关于原点对称,则f(x)是偶函数.( )
(2)若f(x)是偶函数,则它的定义域关于原点对称.( )
(3)若f(-2)=f(2),则f(x)(x∈R)是偶函数.( )
(4)若f(x)(x∈R)是偶函数,则f(-2)=f(2).( )
(5)若f(2)≠f(-2),则f(x)(x∈R)不是偶函数.( )
(6)既是奇函数又是偶函数的函数一定是f(x)=0(x∈R).( )
答案: (1)× (2)√ (3)× (4)√ (5)√ (6)×
解析:只有f(x)的定义域关于原点对称,且f(-x)=f(x)时,f(x)才是偶函数,故(1)错误;
f(x)的定义域关于原点对称是f(x)为偶函数的必要条件,故(2)正确;
对任意x∈R,满足f(-x)=f(x),f(x)才是偶函数,仅凭两个特殊的函数值相等不足以判断函数的奇偶性,故(3)错误而(4)正确;
为了说明f(x)不是偶函数,举一个反例即可,故(5)正确;
f(x)=0,定义域为[-1,1],该函数既是奇函数又是偶函数,故(6)错误.
例1判断下列函数的奇偶性:
分析利用奇函数、偶函数的定义判断函数的奇偶性时,先求出函数的定义域,看其是否关于原点对称,如果定义域关于原点对称,再判断f(-x)与f(x)的关系.为了判断f(-x)与f(x)的关系,既可以从f(-x)开始化简整理,也可以考虑f(-x)+f(x)或f(-x)-f(x)是否等于0.当f(x)不等于0时也可考虑 与1或-1的关系,还可以考虑使用图象法.
一、判断函数的奇偶性
解:(1)函数的定义域为{x|x≠-1},不关于原点对称,故f(x)既不是奇函数又不是偶函数.
(2)函数的定义域为R,关于原点对称,f(-x)=(-x)3-2(-x)=2x-x3=-f(x),∴f(x)是奇函数.
函数的定义域为{-1,1},关于原点对称.
又f(1)=f(-1)=0,故f(x)既是奇函数又是偶函数.
(4)函数的定义域关于原点对称.
(方法一)当x>0时,-x<0,
f(-x)=-x[1-(-x)]=-x(1+x)=-f(x).
当x<0时,-x>0,f(-x)=(-x)[1+(-x)]=-x(1-x)=-f(x).∴f(-x)=-f(x).
∴f(x)是奇函数.
图象关于原点对称,∴f(x)是奇函数.
1.根据奇偶性可将函数分为奇函数,偶函数,既是奇函数也是偶函数,既不是奇函数又不是偶函数.
2.判断函数奇偶性的两种方法
(1)定义法:
(2)图象法:
变式训练判断下列函数的奇偶性:
(2)f(x)=|x+2|+|x-2|;
(3)f(x)=0.
(2)f(x)的定义域是R,又f(-x)=|-x+2|+|-x-2|=|x-2|+|x+2|=f(x),所以f(x)是偶函数.
(3)因为f(x)的定义域为R,又f(-x)=0=f(x),且f(-x)=0=-f(x),所以f(x)既是奇函数又是偶函数.
二、奇、偶函数的运算性质及复合函数的奇偶性
设非零函数f(x),g(x)的定义域分别是F,G,若F=G,则有下列结论:
注意:上述表格中不考虑f(x)±g(x)=0;f[g(x)]中,需x∈G,g(x)∈F.
内偶则偶,内奇同外
偶()偶得偶,奇()奇得奇
同偶异奇
例 已知定义域R上的奇函数,定义在R上偶函数,则下列函数中是奇函数的有( )
C
三、函数奇偶性与单调性的关系
1.奇函数在关于原点对称的区间上具有相同的单调性;偶函数在关于原点对称的区间上具有相反的单调性.上述结论可简记为“奇同偶异”.
2.偶函数在关于原点对称的区间上有相同的最大(小)值,取得最值时的自变量的值互为相反数;奇函数在关于原点对称的区间上取得的最值互为相反数,取得最值时的自变量的值也互为相反数.
微练习
若奇函数f(x)在[-6,-2]上是减函数,且最小值是1,则它在[2,6]上是( )
A.增函数且最小值是-1
B.增函数且最大值是-1
C.减函数且最大值是-1
D.减函数且最小值是-1
答案:C
解析:∵奇函数f(x)在[-6,-2]上是减函数,且最小值是1,∴函数f(x)在[2,6]上是减函数且最大值是-1.
2.设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=( )
A.-1 B.-3 C.1 D.3
答案:B
解析:当x≤0时,f(x)=2x2-x,f(-1)=2×(-1)2-(-1)=3.因为f(x)是定义在R上的奇函数,
故f(1)=-f(-1)=-3,故选B.
1.比较函数值的大小
例3已知偶函数f(x)的定义域为R,当f(x)在区间[0,+∞)上单调递增,则f(-2),f(π),f(-3)的大小关系是( )
A.f(π)>f(-3)>f(-2)
B.f(π)>f(-2)>f(-3)
C.f(π)
解析:∵f(x)在R上是偶函数,∴f(-2)=f(2),f(-3)=f(3).∵2<3<π,且f(x)在区间[0,+∞)上单调递增,
∴f(2)
注意:先利用函数的奇偶性将自变量转化到同一个单调区间上,再根据函数的单调性对函数值的大小作出比较.
延伸探究(1)若将本例中的“增函数”改为“减函数”,其他条件不变,则f(-2),f(π),f(-3)的大小关系如何
(2)若将本例中的“偶函数”改为“奇函数”,其他条件不变,比较这三个函数值的大小.
解:(1)因为当x∈[0,+∞)时,f(x)是减函数,所以有f(2)>f(3)>f(π).又因为f(x)是R上的偶函数,所以f(-2)=f(2),f(-3)=f(3),
从而有f(-2)>f(-3)>f(π).
(2)因为函数为定义在R上的奇函数,且在[0,+∞)上单调递增,所以函数在R上是增函数,
因为-3<-2<π,所以f(-3)
例4已知定义在区间[-2,2]上的奇函数f(x)在区间[0,2]上单调递增,若f(1-m)
反思感悟解有关奇函数f(x)的不等式f(a)+f(b)<0,先将f(a)+f(b)<0变形为f(a)<-f(b)=f(-b),再利用f(x)的单调性去掉“f”,化为关于a,b的不等式.另外,要特别注意函数的定义域.
由于偶函数在关于原点对称的两个区间上的单调性相反,所以我们要利用偶函数的性质f(x)=f(|x|)=f(-|x|)将f(g(x))中的g(x)全部化到同一个单调区间内,再利用单调性去掉符号f,使不等式得解.
延伸探究若将本例中的“奇函数”改为“偶函数”,把区间“[0,2]”改为“[-2,0]”,其他条件不变,求实数m的取值范围.
解:因为函数为[-2,2]上的偶函数,又函数在[-2,0]上单调递减,所以函数在[0,2]上单调递增,
不等式可化为f(|1-m|)
3.函数f(x)的定义域为R,且对任意x∈R,有f(x)满足f(-x)=f(x),且f(x)在区间(-∞,-1]上单调递增,则( )
例2已知f(x)为R上的奇函数,当x>0时,f(x)=-2x2+3x+1.
(1)求f(-1);
(2)求f(x)的解析式.
分析(1)根据奇函数的性质,将f(-1)转化为f(1)求解;(2)先设出所求区间上的自变量,利用奇函数、偶函数的定义域关于原点对称的特点,把它转化到已知解析式的区间上,代入已知的解析式,再次利用函数的奇偶性求解.注意不要忽略x=0时f(x)的解析式.
四、利用函数的奇偶性求解析式
解:(1)因为函数f(x)为奇函数,
所以f(-1)=-f(1)=-(-2×12+3×1+1)=-2.
(2)当x<0时,-x>0,则
f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.
由于f(x)是奇函数,则f(x)=-f(-x),
所以f(x)=2x2+3x-1.当x=0时,f(-0)=-f(0),则f(0)=-f(0),即f(0)=0.
反思感悟1.这类问题常见的情形是:
已知当x∈(a,b)时,f(x)=φ(x),求当x∈(-b,-a)时f(x)的解析式.
若f(x)为奇函数,则当x∈(-b,-a)时,
f(x)=-f(-x)=-φ(-x);
若f(x)为偶函数,则当x∈(-b,-a)时,
f(x)=f(-x)=φ(-x).
2.若函数f(x)的定义域内含0且为奇函数,则必有f(0)=0,不能漏掉.
延伸探究若将本例中的“奇”改为“偶”,“x>0”改为“x≥0”,其他条件不变,求f(x)的解析式.
解:当x<0时,-x>0,此时f(-x)=-2(-x)2+3(-x)+1=-2x2-3x+1.由于f(x)是偶函数,则f(x)=f(-x)=-2x2-3x+1,所以f(x)的解析式为
五、利用定义法、赋值法解决抽象函数奇偶性问题
典例1若定义在R上的函数f(x)满足:对任意的x1,x2∈R,都有f(x1+x2)=f(x1)+f(x2),且当x>0时,f(x)<0,则( )
A.f(x)是奇函数,且在R上是增函数
B.f(x)是奇函数,且在R上是减函数
C.f(x)是奇函数,且在R上不是单调函数
D.无法确定f(x)的单调性和奇偶性
解析:令x1=x2=0,则f(0)=2f(0),所以f(0)=0.
令x1=x,x2=-x,
则f(-x)+f(x)=f(x-x)=f(0)=0,
所以f(-x)=-f(x),故函数y=f(x)是奇函数.
设x1
故f(x2)
答案:B
典例2已知函数f(x),x∈R,若对于任意实数x1,x2,都有f(x1+x2)+f(x1-x2)=2f(x1)·f(x2),
求证:函数f(x)为偶函数.
证明:令x1=0,x2=x,得f(x)+f(-x)=2f(0)f(x).①
令x2=0,x1=x,得f(x)+f(x)=2f(0)f(x).②
由①②得f(x)+f(-x)=f(x)+f(x),即f(-x)=f(x),所以函数f(x)为偶函数.
反思感悟1.判断抽象函数的奇偶性,应利用函数奇偶性的定义,找准方向,巧妙赋值,合理、灵活变形,找出f(-x)与f(x)的关系,从而判断或证明抽象函数的奇偶性.
2.有时需要在整体上研究f(-x)+f(x)的和的情况.
比如:上面典例1中利用f(-x)+f(x)=0可得出y=f(x)是奇函数.
变式训练定义在R上的函数y=f(x)满足:对任意α,β∈R,总有f(α+β)-[f(α)+f(β)]=2 019,则下列说法正确的是( )
A.f(x)-1是奇函数
B.f(x)+1是奇函数
C.f(x)-2 019是奇函数
D.f(x)+2 019是奇函数
答案:D
解析:令α=β=0,则f(0)-[f(0)+f(0)]=2 019,
即f(0)=-2 019.
令β=-α,则f(0)-[f(α)+f(-α)]=2 019,
即f(α)+f(-α)=-4 038,
则f(-α)+2 019=-2 019-f(α)=-[2 019+f(α)],
即f(x)+2 019是奇函数,故选D.
课堂小结
偶函数 奇函数
定义
图象
定义域
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),
一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),
关于y轴对称
关于原点对称
关于原点对称
用定义法判断函数的奇偶性的步骤:
①首先确定函数的定义域,并判断其定义域是否关于原点对称;
②确定f(-x)和f(x)的关系;
③作出相应结论。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
