5.4 平行线的性质定理和判定定理课件(共17张PPT)2023-2024学年青岛版数学八年级上册
文档属性
| 名称 | 5.4 平行线的性质定理和判定定理课件(共17张PPT)2023-2024学年青岛版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 388.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第5章 几何证明初步
5.4 平行线的性质定理和判定定理
学习目标
掌握平行线的性质定理和判定定理的证明.会区分平行线的判定定理及性质定理,体会二者之间的区别与联系;
了解互逆命题的概念,知道原命题成立时,逆命题不一定成立.了解逆定理的概念;
培养观察能力与语言表达能力.
温故知新
我们曾探索了哪些平行线的性质和判定方法?
(1)两条平行直线被第三条直线所截,同位角相等;
1.平行线的性质:
(2)两条平行直线被第三条直线所截,内错角相等;
(3)两条平行直线被第三条直线所截,同旁内角互补.
2.平行线的判定方法:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行;
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行.
新课探究
利用它和其他有关的基本事实,可以证明平行线的性质定理1“两条平行直线被第三条直线所截,同位角相等”.
上面哪一项是基本事实?
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
那么怎么用这个性质定理、有关基本事实及已证实的定理证明平行线的其他性质和判定方法呢?
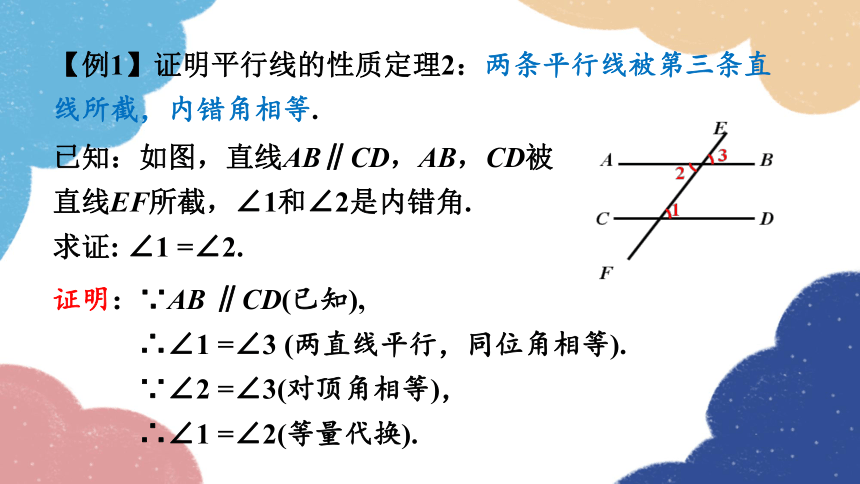
【例1】证明平行线的性质定理2:两条平行线被第三条直线所截,内错角相等.
已知:如图,直线AB∥CD,AB,CD被直线EF所截,∠1和∠2是内错角.
求证: ∠1 =∠2.
证明:∵AB ∥CD(已知),
∴∠1 =∠3 (两直线平行,同位角相等).
∵∠2 =∠3(对顶角相等),
∴∠1 =∠2(等量代换).
【例2】证明平行线的判定定理2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.
求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1=∠3 (对顶角相等),
∴∠2=∠3 (等量代换).
∴ a∥b(同位角相等,两直线平行).
你能自己证明其余的平行线的性质定理与判定定理吗?试试看看.
对于我们刚刚证明的两个命题,你发现它们的条件和结论之间有什么关系?
(1)两条平行直线被第三条直线所截,内错角相等;
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行.
两个命题的条件和结论正好互相交换.
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题叫做它的逆命题.
上面所说的两个命题是互逆命题.
若把命题(1)叫做原命题,则命题(2)叫做命题(1)的逆命题.
若把命题(2)叫做原命题,则命题(1)叫做命题(2)的逆命题.
如果一个定理的逆命题也是真命题,那么这个逆命题就是原定理的逆定理.
(1)互逆命题的真假没有必然的联系,原命题为真,逆命题不一定为真;原命题为假,逆命题不一定为假.
注意:
(2)任何一个命题都有逆命题,但是逆命题不一定正确,所以并不是每一个定理都有逆定理.
【例3】写出命题“全等三角形的对应边相等”的逆命题.
解:逆命题:如果两个三角形的三边分别对应相等,那么它们是全等三角形.
注意:写一个命题的逆命题时,除把条件和结论进行交换外,还要注意语句是否通顺,不要机械地照搬原命题中的条件和结论两部分,造成命题语句不通的错误.
课堂练习
1.下列定理中,逆定理不存在的是( )
A.角平分线上的点到这个角两边的距离相等
B.内错角相等,两直线平行
C.同位角相等,两直线平行
D.全等三角形的周长相等
分析:D、逆命题:周长相等的三角形全等,不正确,也就是逆定理不存在.
D
2.写出下列命题的逆命题,并判断它的逆命题的真假.
(1)直角都相等;
(2)若x=1.则x2=1.
解: (1)它的逆命题为:相等的角都是直角.这是一个假命题.反例:∠1=∠2=30°,符和其条件,不符合其结论.
(2)它的逆命题为:若x2=1,则x=1.这是一个假命题.因为x=-1满足它的条件,不满足它的结论.
3.已知:如下图所示,∠1=∠A,∠2=∠B.
求证:MN∥EF.
证明:∵∠1=∠A(已知),
∴MN∥AB(内错角相等,两直线平行).
∵∠2=∠B(已知),
∴ EF∥AB(同位角相等,两直线平行).
∴ MN∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
课堂小结
1.平行线的性质定理和判定定理的证明.
2.互逆命题、原命题、逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题叫做它的逆命题.
3. 逆定理
如果一个定理的逆命题也是真命题,那么这个逆命题就是原定理的逆定理.
(1)互逆命题的真假没有必然的联系.
(2)任一个命题都有逆命题,不是每一个定理都有逆定理.
(3)写一个命题的逆命题时,除把条件和结论进行交换
外,还要注意语句是否通顺.
谢谢!
第5章 几何证明初步
5.4 平行线的性质定理和判定定理
学习目标
掌握平行线的性质定理和判定定理的证明.会区分平行线的判定定理及性质定理,体会二者之间的区别与联系;
了解互逆命题的概念,知道原命题成立时,逆命题不一定成立.了解逆定理的概念;
培养观察能力与语言表达能力.
温故知新
我们曾探索了哪些平行线的性质和判定方法?
(1)两条平行直线被第三条直线所截,同位角相等;
1.平行线的性质:
(2)两条平行直线被第三条直线所截,内错角相等;
(3)两条平行直线被第三条直线所截,同旁内角互补.
2.平行线的判定方法:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行;
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行;
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行.
新课探究
利用它和其他有关的基本事实,可以证明平行线的性质定理1“两条平行直线被第三条直线所截,同位角相等”.
上面哪一项是基本事实?
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.
那么怎么用这个性质定理、有关基本事实及已证实的定理证明平行线的其他性质和判定方法呢?
【例1】证明平行线的性质定理2:两条平行线被第三条直线所截,内错角相等.
已知:如图,直线AB∥CD,AB,CD被直线EF所截,∠1和∠2是内错角.
求证: ∠1 =∠2.
证明:∵AB ∥CD(已知),
∴∠1 =∠3 (两直线平行,同位角相等).
∵∠2 =∠3(对顶角相等),
∴∠1 =∠2(等量代换).
【例2】证明平行线的判定定理2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.
求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1=∠3 (对顶角相等),
∴∠2=∠3 (等量代换).
∴ a∥b(同位角相等,两直线平行).
你能自己证明其余的平行线的性质定理与判定定理吗?试试看看.
对于我们刚刚证明的两个命题,你发现它们的条件和结论之间有什么关系?
(1)两条平行直线被第三条直线所截,内错角相等;
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行.
两个命题的条件和结论正好互相交换.
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题叫做它的逆命题.
上面所说的两个命题是互逆命题.
若把命题(1)叫做原命题,则命题(2)叫做命题(1)的逆命题.
若把命题(2)叫做原命题,则命题(1)叫做命题(2)的逆命题.
如果一个定理的逆命题也是真命题,那么这个逆命题就是原定理的逆定理.
(1)互逆命题的真假没有必然的联系,原命题为真,逆命题不一定为真;原命题为假,逆命题不一定为假.
注意:
(2)任何一个命题都有逆命题,但是逆命题不一定正确,所以并不是每一个定理都有逆定理.
【例3】写出命题“全等三角形的对应边相等”的逆命题.
解:逆命题:如果两个三角形的三边分别对应相等,那么它们是全等三角形.
注意:写一个命题的逆命题时,除把条件和结论进行交换外,还要注意语句是否通顺,不要机械地照搬原命题中的条件和结论两部分,造成命题语句不通的错误.
课堂练习
1.下列定理中,逆定理不存在的是( )
A.角平分线上的点到这个角两边的距离相等
B.内错角相等,两直线平行
C.同位角相等,两直线平行
D.全等三角形的周长相等
分析:D、逆命题:周长相等的三角形全等,不正确,也就是逆定理不存在.
D
2.写出下列命题的逆命题,并判断它的逆命题的真假.
(1)直角都相等;
(2)若x=1.则x2=1.
解: (1)它的逆命题为:相等的角都是直角.这是一个假命题.反例:∠1=∠2=30°,符和其条件,不符合其结论.
(2)它的逆命题为:若x2=1,则x=1.这是一个假命题.因为x=-1满足它的条件,不满足它的结论.
3.已知:如下图所示,∠1=∠A,∠2=∠B.
求证:MN∥EF.
证明:∵∠1=∠A(已知),
∴MN∥AB(内错角相等,两直线平行).
∵∠2=∠B(已知),
∴ EF∥AB(同位角相等,两直线平行).
∴ MN∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
课堂小结
1.平行线的性质定理和判定定理的证明.
2.互逆命题、原命题、逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,那么另一命题叫做它的逆命题.
3. 逆定理
如果一个定理的逆命题也是真命题,那么这个逆命题就是原定理的逆定理.
(1)互逆命题的真假没有必然的联系.
(2)任一个命题都有逆命题,不是每一个定理都有逆定理.
(3)写一个命题的逆命题时,除把条件和结论进行交换
外,还要注意语句是否通顺.
谢谢!
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
