人教版七年级下册数学课时练10.2 直方图 课时练(含答案)
文档属性
| 名称 | 人教版七年级下册数学课时练10.2 直方图 课时练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 179.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览


文档简介
人教版七年级下册数学
《10.2 直方图》课时练
一、选择题
1.将50个数据分成3组,其中第一组和第三组的频率之和为0.7,则第二小组的频数是( )
A.0.3 B.0.7 C.15 D.35
2.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/min 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 20 16 9 5
则通话时间不超过15min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
4.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在25~30次的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
5.一个容量为70的样本最大值为141,最小值60,取组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
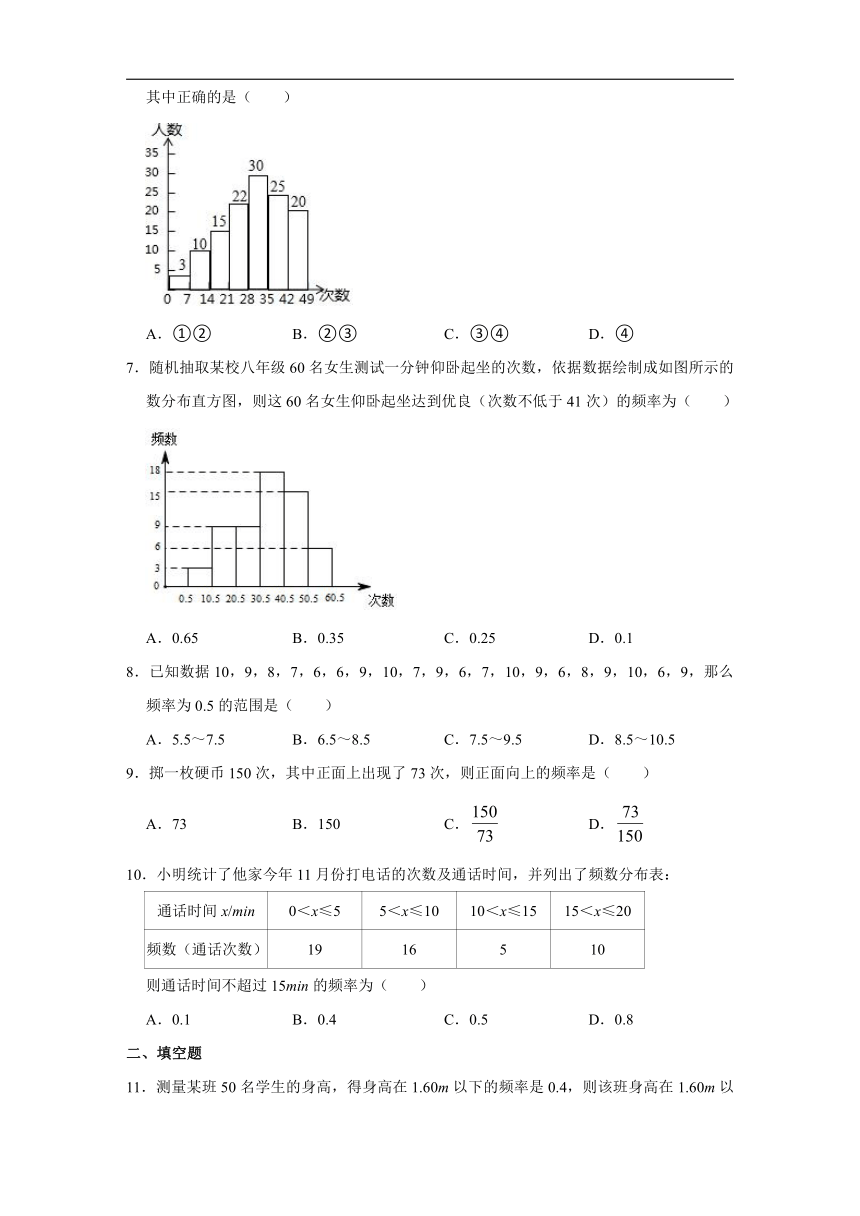
6.小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法:
①这栋居民楼共有居民140人
②每周使用手机支付次数为28~35次的人数最多
③有的人每周使用手机支付的次数在35~42次
④每周使用手机支付不超过21次的有15人
其中正确的是( )
A.①② B.②③ C.③④ D.④
7.随机抽取某校八年级60名女生测试一分钟仰卧起坐的次数,依据数据绘制成如图所示的数分布直方图,则这60名女生仰卧起坐达到优良(次数不低于41次)的频率为( )
A.0.65 B.0.35 C.0.25 D.0.1
8.已知数据10,9,8,7,6,6,9,10,7,9,6,7,10,9,6,8,9,10,6,9,那么频率为0.5的范围是( )
A.5.5~7.5 B.6.5~8.5 C.7.5~9.5 D.8.5~10.5
9.掷一枚硬币150次,其中正面上出现了73次,则正面向上的频率是( )
A.73 B.150 C. D.
10.小明统计了他家今年11月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/min 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 19 16 5 10
则通话时间不超过15min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.8
二、填空题
11.测量某班50名学生的身高,得身高在1.60m以下的频率是0.4,则该班身高在1.60m以下的学生有 人.
12.一个样本的50个数据分别落在5个小组内,第1、2、3、4组的数据的个数分别为2、8、15、5,则第5组的频率为 .
13.一个容量为40的样本的最大值为35,最小值为10,若取组距为4,则应该分的组数为 .
14.一个样本容量为80的样本最大值是123,最小值是50,取10为组距,则可分为 组.
15.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.
某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 班
三、解答题
16.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
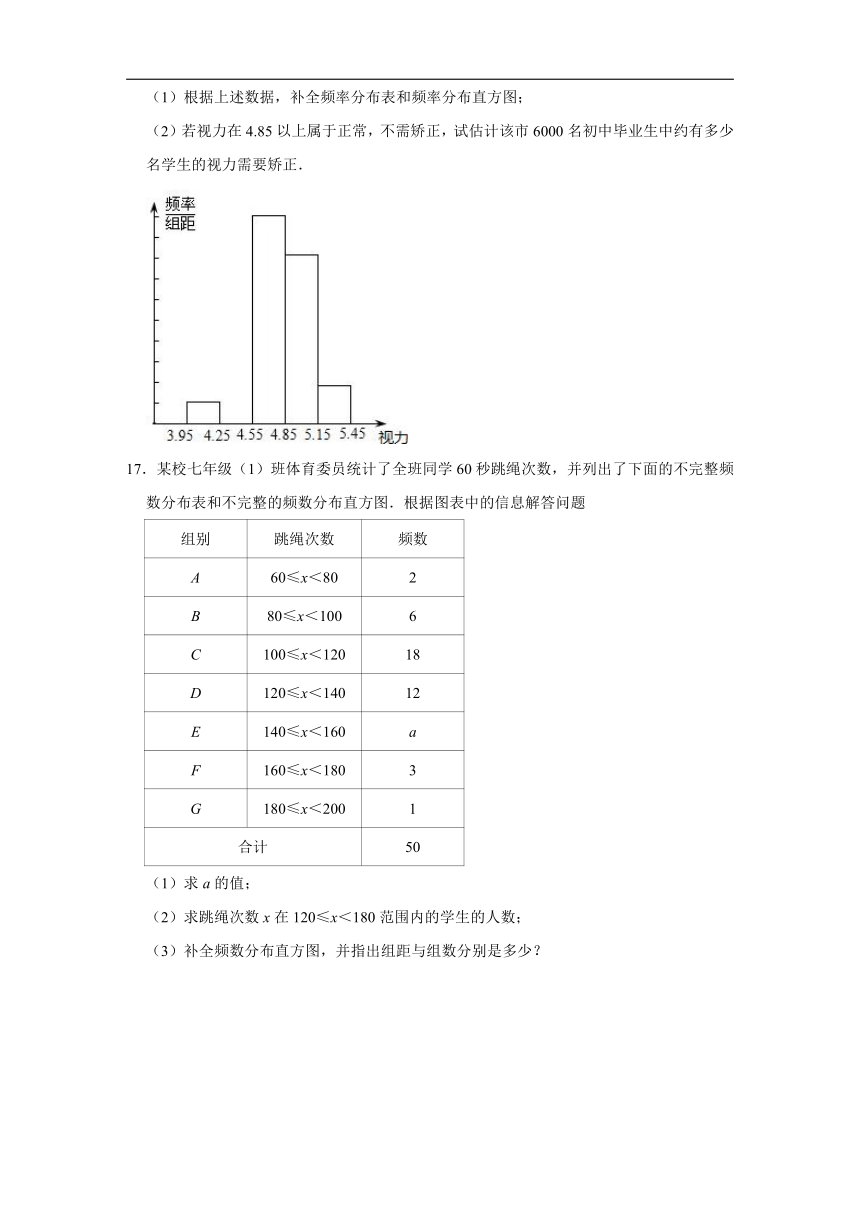
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
17.某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 跳绳次数 频数
A 60≤x<80 2
B 80≤x<100 6
C 100≤x<120 18
D 120≤x<140 12
E 140≤x<160 a
F 160≤x<180 3
G 180≤x<200 1
合计 50
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?
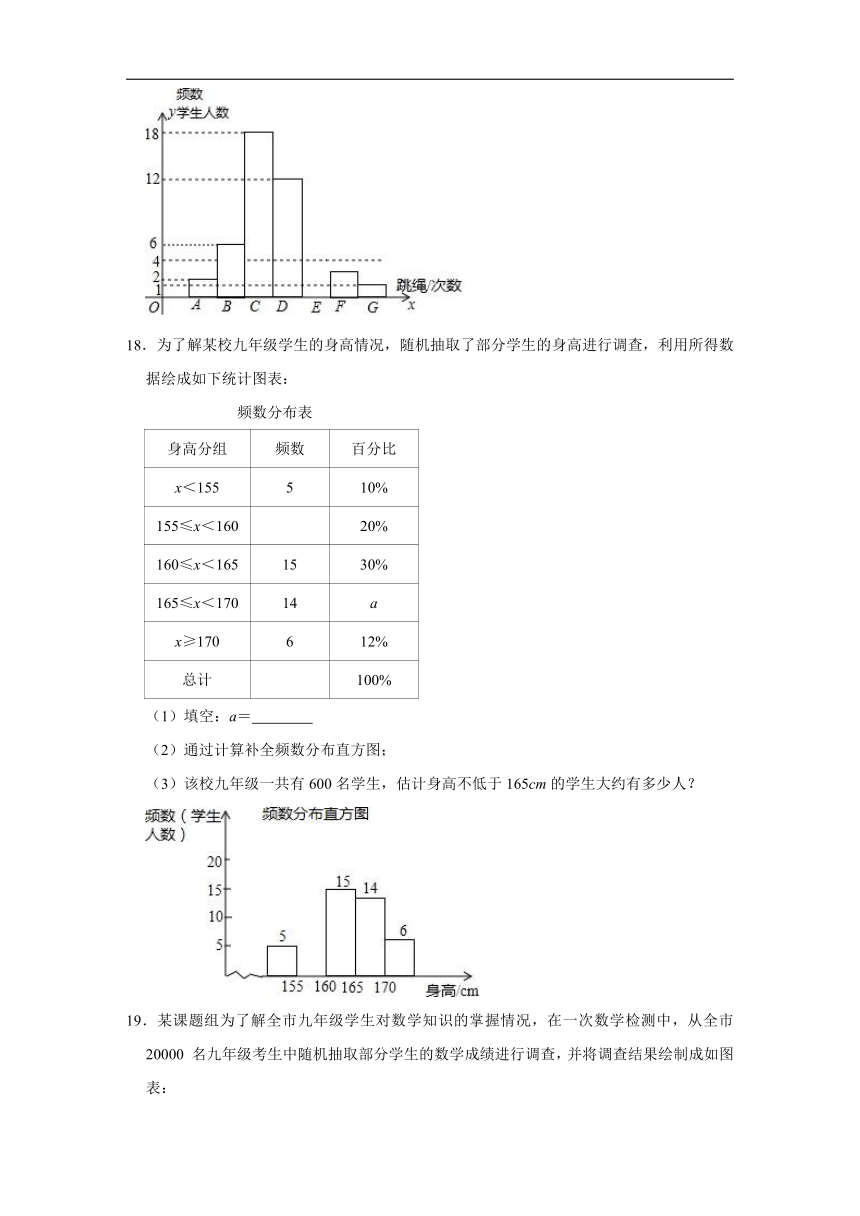
18.为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组 频数 百分比
x<155 5 10%
155≤x<160 20%
160≤x<165 15 30%
165≤x<170 14 a
x≥170 6 12%
总计 100%
(1)填空:a=
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?
19.某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
分数段 频数 频率
50≤x≤60 20 0.10
60≤x≤70 28 b
70≤x≤80 54 0.27
80≤x≤90 a 0.20
90≤x≤100 24 0.12
100≤x≤110 18 0.09
110≤x≤120 16 0.08
(1)表中a和b所表示的数分别为:a= ,b= ;
(2)请在图中补全额数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
20.国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.国家创新指数得分在60≤x<70这一组的是:
61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第 ;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线l1的上方,请在图中用“〇”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为 万美元;(结果保留一位小数)
(4)下列推断合理的是 .
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
参考答案
1.C 2.C 3.D 4.D 5.B 6.B 7.B 8.D 9.D 10.D
11.20
12.0.4.
13.7.
14.8.
15.甲.
16.解:(1)样本容量=2÷0.04=50,
4.55﹣4.85的频数=50×0.40=20;
如图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 20 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 50 1
(2)6000×(0.04+0.16+0.40)=3600(名),
∴约有3600名学生的视力需要矫正.
17.解:(1)a=50﹣(2+6+18+12+3+1)=8;
(2)跳绳次数x在120≤x<180范围内的学生的人数为12+8+3=23人;
(3)补全图形如下:
组距为20、组数为7.
18.解:(1)由表格可得,调查的总人数为:5÷10%=50,
a=14÷50×100%=28%,
故答案为:28%;
(2)155≤x<160的人数是:50×20%=10(人),补图如下:
(3)根据题意得:
600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的学生大约有240人.
19.解:(1)∵总数为20÷0.1=200,
∴b=28÷200=0.14,a=200×0.2=40,
故答案为:40,0.14;
(2)如图:
;
(3)(0.27+0.20+0.12+0.09+0.08)×20000
=0.76×20000
=15200(人)
答:该市20000名九年级考生数学成绩为合格的学生约有15200名.
20.解:(1)∵国家创新指数得分为69.5以上(含69.5)的国家有17个,
∴国家创新指数得分排名前40的国家中,中国的国家创新指数得分排名世界第17,
故答案为:17;
(2)如图所示:
(3)由40个国家的人均国内生产总值和国家创新指数得分情况统计图可知,在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为2.8万美元;
故答案为:2.8;
(4)由40个国家的人均国内生产总值和国家创新指数得分情况统计图可知,
①相比于点A、B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;合理;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值;合理;
故答案为:①②.
《10.2 直方图》课时练
一、选择题
1.将50个数据分成3组,其中第一组和第三组的频率之和为0.7,则第二小组的频数是( )
A.0.3 B.0.7 C.15 D.35
2.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/min 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 20 16 9 5
则通话时间不超过15min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
4.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在25~30次的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
5.一个容量为70的样本最大值为141,最小值60,取组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
6.小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法:
①这栋居民楼共有居民140人
②每周使用手机支付次数为28~35次的人数最多
③有的人每周使用手机支付的次数在35~42次
④每周使用手机支付不超过21次的有15人
其中正确的是( )
A.①② B.②③ C.③④ D.④
7.随机抽取某校八年级60名女生测试一分钟仰卧起坐的次数,依据数据绘制成如图所示的数分布直方图,则这60名女生仰卧起坐达到优良(次数不低于41次)的频率为( )
A.0.65 B.0.35 C.0.25 D.0.1
8.已知数据10,9,8,7,6,6,9,10,7,9,6,7,10,9,6,8,9,10,6,9,那么频率为0.5的范围是( )
A.5.5~7.5 B.6.5~8.5 C.7.5~9.5 D.8.5~10.5
9.掷一枚硬币150次,其中正面上出现了73次,则正面向上的频率是( )
A.73 B.150 C. D.
10.小明统计了他家今年11月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/min 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 19 16 5 10
则通话时间不超过15min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.8
二、填空题
11.测量某班50名学生的身高,得身高在1.60m以下的频率是0.4,则该班身高在1.60m以下的学生有 人.
12.一个样本的50个数据分别落在5个小组内,第1、2、3、4组的数据的个数分别为2、8、15、5,则第5组的频率为 .
13.一个容量为40的样本的最大值为35,最小值为10,若取组距为4,则应该分的组数为 .
14.一个样本容量为80的样本最大值是123,最小值是50,取10为组距,则可分为 组.
15.某中学七年级甲、乙、丙三个班中,每班的学生人数都为40名.
某次数学考试的成绩统计如下:(如图,每组分数含最小值,不含最大值)根据图、表提供的信息,则80~90分这一组人数最多的班是 班
三、解答题
16.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
17.某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 跳绳次数 频数
A 60≤x<80 2
B 80≤x<100 6
C 100≤x<120 18
D 120≤x<140 12
E 140≤x<160 a
F 160≤x<180 3
G 180≤x<200 1
合计 50
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?
18.为了解某校九年级学生的身高情况,随机抽取了部分学生的身高进行调查,利用所得数据绘成如下统计图表:
频数分布表
身高分组 频数 百分比
x<155 5 10%
155≤x<160 20%
160≤x<165 15 30%
165≤x<170 14 a
x≥170 6 12%
总计 100%
(1)填空:a=
(2)通过计算补全频数分布直方图;
(3)该校九年级一共有600名学生,估计身高不低于165cm的学生大约有多少人?
19.某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如图表:
分数段 频数 频率
50≤x≤60 20 0.10
60≤x≤70 28 b
70≤x≤80 54 0.27
80≤x≤90 a 0.20
90≤x≤100 24 0.12
100≤x≤110 18 0.09
110≤x≤120 16 0.08
(1)表中a和b所表示的数分别为:a= ,b= ;
(2)请在图中补全额数分布直方图;
(3)如果把成绩在70分以上(含70分)定为合格,那么该市20000名九年级考生数学成绩为合格的学生约有多少名?
20.国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频数分布直方图(数据分成7组:30≤x<40,40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.国家创新指数得分在60≤x<70这一组的是:
61.7 62.4 63.6 65.9 66.4 68.5 69.1 69.3 69.5
c.40个国家的人均国内生产总值和国家创新指数得分情况统计图:
d.中国的国家创新指数得分为69.5.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,回答下列问题:
(1)中国的国家创新指数得分排名世界第 ;
(2)在40个国家的人均国内生产总值和国家创新指数得分情况统计图中,包括中国在内的少数几个国家所对应的点位于虚线l1的上方,请在图中用“〇”圈出代表中国的点;
(3)在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为 万美元;(结果保留一位小数)
(4)下列推断合理的是 .
①相比于点A,B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
参考答案
1.C 2.C 3.D 4.D 5.B 6.B 7.B 8.D 9.D 10.D
11.20
12.0.4.
13.7.
14.8.
15.甲.
16.解:(1)样本容量=2÷0.04=50,
4.55﹣4.85的频数=50×0.40=20;
如图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 20 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 50 1
(2)6000×(0.04+0.16+0.40)=3600(名),
∴约有3600名学生的视力需要矫正.
17.解:(1)a=50﹣(2+6+18+12+3+1)=8;
(2)跳绳次数x在120≤x<180范围内的学生的人数为12+8+3=23人;
(3)补全图形如下:
组距为20、组数为7.
18.解:(1)由表格可得,调查的总人数为:5÷10%=50,
a=14÷50×100%=28%,
故答案为:28%;
(2)155≤x<160的人数是:50×20%=10(人),补图如下:
(3)根据题意得:
600×(28%+12%)=600×40%=240(人)
即该校九年级共有600名学生,身高不低于165cm的学生大约有240人.
19.解:(1)∵总数为20÷0.1=200,
∴b=28÷200=0.14,a=200×0.2=40,
故答案为:40,0.14;
(2)如图:
;
(3)(0.27+0.20+0.12+0.09+0.08)×20000
=0.76×20000
=15200(人)
答:该市20000名九年级考生数学成绩为合格的学生约有15200名.
20.解:(1)∵国家创新指数得分为69.5以上(含69.5)的国家有17个,
∴国家创新指数得分排名前40的国家中,中国的国家创新指数得分排名世界第17,
故答案为:17;
(2)如图所示:
(3)由40个国家的人均国内生产总值和国家创新指数得分情况统计图可知,在国家创新指数得分比中国高的国家中,人均国内生产总值的最小值约为2.8万美元;
故答案为:2.8;
(4)由40个国家的人均国内生产总值和国家创新指数得分情况统计图可知,
①相比于点A、B所代表的国家,中国的国家创新指数得分还有一定差距,中国提出“加快建设创新型国家”的战略任务,进一步提高国家综合创新能力;合理;
②相比于点B,C所代表的国家,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值;合理;
故答案为:①②.
