3.1.2 椭圆的简单几何性质(第2课时) 课件(共38张PPT)
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质(第2课时) 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 21:04:11 | ||
图片预览










文档简介
3.1.2 椭圆的简单几何性质(第2课时)
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.根据几何条件求出椭圆的方程;
2.进一步掌握椭圆的方程及其性质的应用;
3.会判断直线与椭圆的位置关系.
01导入
PART ONE
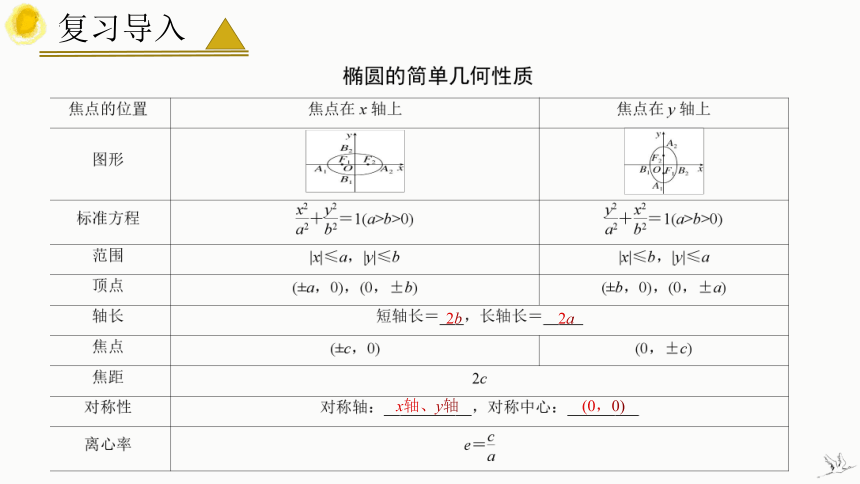
2b
2a
x轴、y轴
(0,0)
复习导入
02 点、直线与椭圆位置关系
PART ONE
点、直线与椭圆位置关系
探究1:根据点与圆的位置关系,你能得出点P(x0,y0)与椭圆????2????2+????2????2=1(a>b>0)的位置关系有哪些?怎样判断?
?
点与椭圆的位置关系有三种:点P在椭圆上;点P在椭圆内部;点P在椭圆外部。
点P(x0,y0)与椭圆????2????2+????2????2=1(a>b>0)的位置关系:
(1)点P在椭圆上?????02????2+????02????2 1;
(2)点P在椭圆内部?????02????2+????02????2 1;
(3)点P在椭圆外部?????02????2+????02????2 1.
?
=
<
>
点、直线与椭圆位置关系
练习1.点(1,1)与椭圆????2????2+????2????2=1的位置关系为( )
A.在椭圆上 B.在椭圆内 C.在椭圆外 D.不能确定
?
练习2.若点A(a,1)在椭圆????24+????22=1的内部,则a的取值范围是________.
?
牛刀小试
点、直线与椭圆位置关系
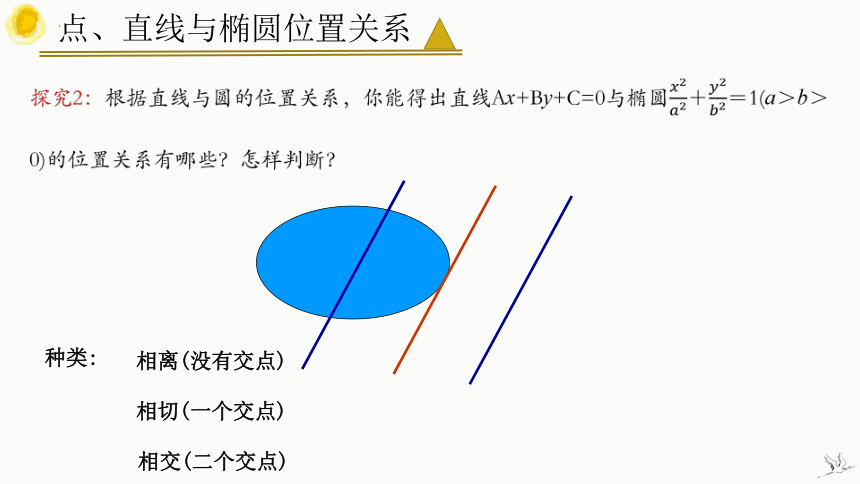
探究2:根据直线与圆的位置关系,你能得出直线Ax+By+C=0与椭圆????2????2+????2????2=1(a>b>0)的位置关系有哪些?怎样判断?
?
种类:
相离(没有交点)
相切(一个交点)
相交(二个交点)
点、直线与椭圆位置关系
mx2+nx+p=0(m≠ 0)
<0
方程组无解
相离
无交点
=0
方程组有一解
相切
一个交点
>0
相交
方程组有两解
两个交点
代数方法
= n2-4mp
Ax+By+C=0
由方程组:
????2????2
????2????2=1
?
点、直线与椭圆位置关系
点、直线与椭圆位置关系
点、直线与椭圆位置关系
点、直线与椭圆位置关系
03 弦长问题
PART ONE
弦长问题
如图示,若直线l与椭圆交于A, B两点,将直线方程与椭圆方程联立消元,得到关于x(或y)的一元二次方程,然后运用两点间距离公式及根与系数的关系,即可求弦长。
O
x
y
F2
l
?
F1
?
A
B
特别地,当直线斜率不存在是,则
弦长问题
弦长问题
弦长问题
归纳总结
直线与椭圆有关相交弦的问题
主要思路是联立直线和椭圆的方程,得到一元二次方程,然后借助一元二次方程的有关知识解决,有时运用弦长公式,解题时应注意以下几点:
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.
(2)当弦的两端点的坐标不易求时,可用弦长公式.
(3)如果直线方程涉及斜率,要注意斜率不存在的情况.
弦长问题
弦长问题
弦长问题
弦长问题
04 中点弦问题
PART ONE
中点弦问题
O
x
y
F2
l
?
F1
?
P
?
B
A
中点弦问题
中点弦问题
中点弦问题
归纳总结
中点弦问题
C
中点弦问题
05与椭圆有关的实际问题
PART ONE
实际应用
?
?
实际应用
?
实际应用
利用椭圆的几何性质求标准方程的思路
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离
的比是常数 求动点M的轨迹.
O
x
y
M
H
F
l
?
d
解:
∴点M的轨迹为长轴、短轴分别为10和6的椭圆。
实际应用
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
O
x
y
M
H
F
l
?
d
l′
F′
?
椭圆的第二定义:
实际应用
实际应用
O
x
y
M
H
F
l
?
d
l′
F′
?
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
06课堂小结
PART ONE
课堂小结
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.根据几何条件求出椭圆的方程;
2.进一步掌握椭圆的方程及其性质的应用;
3.会判断直线与椭圆的位置关系.
01导入
PART ONE
2b
2a
x轴、y轴
(0,0)
复习导入
02 点、直线与椭圆位置关系
PART ONE
点、直线与椭圆位置关系
探究1:根据点与圆的位置关系,你能得出点P(x0,y0)与椭圆????2????2+????2????2=1(a>b>0)的位置关系有哪些?怎样判断?
?
点与椭圆的位置关系有三种:点P在椭圆上;点P在椭圆内部;点P在椭圆外部。
点P(x0,y0)与椭圆????2????2+????2????2=1(a>b>0)的位置关系:
(1)点P在椭圆上?????02????2+????02????2 1;
(2)点P在椭圆内部?????02????2+????02????2 1;
(3)点P在椭圆外部?????02????2+????02????2 1.
?
=
<
>
点、直线与椭圆位置关系
练习1.点(1,1)与椭圆????2????2+????2????2=1的位置关系为( )
A.在椭圆上 B.在椭圆内 C.在椭圆外 D.不能确定
?
练习2.若点A(a,1)在椭圆????24+????22=1的内部,则a的取值范围是________.
?
牛刀小试
点、直线与椭圆位置关系
探究2:根据直线与圆的位置关系,你能得出直线Ax+By+C=0与椭圆????2????2+????2????2=1(a>b>0)的位置关系有哪些?怎样判断?
?
种类:
相离(没有交点)
相切(一个交点)
相交(二个交点)
点、直线与椭圆位置关系
mx2+nx+p=0(m≠ 0)
<0
方程组无解
相离
无交点
=0
方程组有一解
相切
一个交点
>0
相交
方程组有两解
两个交点
代数方法
= n2-4mp
Ax+By+C=0
由方程组:
????2????2
????2????2=1
?
点、直线与椭圆位置关系
点、直线与椭圆位置关系
点、直线与椭圆位置关系
点、直线与椭圆位置关系
03 弦长问题
PART ONE
弦长问题
如图示,若直线l与椭圆交于A, B两点,将直线方程与椭圆方程联立消元,得到关于x(或y)的一元二次方程,然后运用两点间距离公式及根与系数的关系,即可求弦长。
O
x
y
F2
l
?
F1
?
A
B
特别地,当直线斜率不存在是,则
弦长问题
弦长问题
弦长问题
归纳总结
直线与椭圆有关相交弦的问题
主要思路是联立直线和椭圆的方程,得到一元二次方程,然后借助一元二次方程的有关知识解决,有时运用弦长公式,解题时应注意以下几点:
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.
(2)当弦的两端点的坐标不易求时,可用弦长公式.
(3)如果直线方程涉及斜率,要注意斜率不存在的情况.
弦长问题
弦长问题
弦长问题
弦长问题
04 中点弦问题
PART ONE
中点弦问题
O
x
y
F2
l
?
F1
?
P
?
B
A
中点弦问题
中点弦问题
中点弦问题
归纳总结
中点弦问题
C
中点弦问题
05与椭圆有关的实际问题
PART ONE
实际应用
?
?
实际应用
?
实际应用
利用椭圆的几何性质求标准方程的思路
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
例6 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离
的比是常数 求动点M的轨迹.
O
x
y
M
H
F
l
?
d
解:
∴点M的轨迹为长轴、短轴分别为10和6的椭圆。
实际应用
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
O
x
y
M
H
F
l
?
d
l′
F′
?
椭圆的第二定义:
实际应用
实际应用
O
x
y
M
H
F
l
?
d
l′
F′
?
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
06课堂小结
PART ONE
课堂小结
