3.2.2 双曲线的简单几何性质(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(第2课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 30.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 21:05:59 | ||
图片预览








文档简介
(共23张PPT)
3.2.2 双曲线的简单几何性质
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
01情景导入
PART ONE
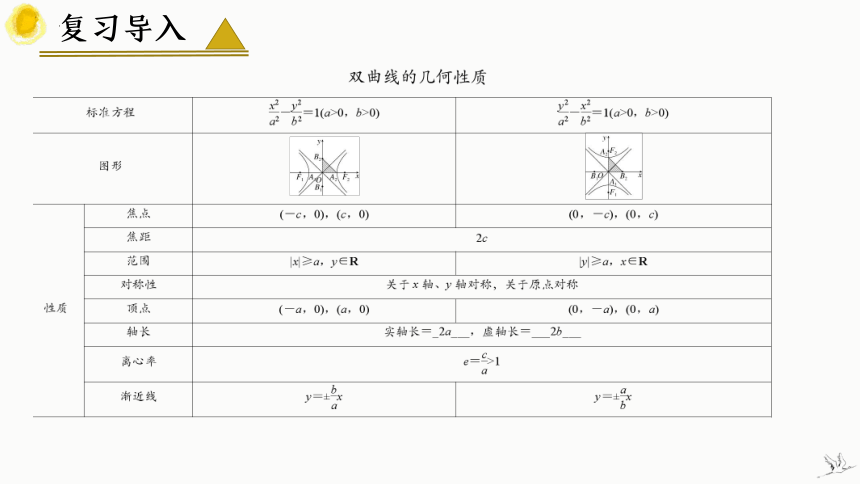
复习导入
复习导入
02双曲线的简单的几何性质
渐近线
PART ONE
双曲线的简单几何性质
y=±2x
求双曲线渐近线
双曲线的简单几何性质
双曲线的简单几何性质
方法总结
双曲线的简单几何性质
AD
双曲线的简单几何性质
双曲线的简单几何性质
C
03双曲线的简单的几何性质
离心率
PART ONE
双曲线的简单几何性质
例2. (1)已知双曲线的两条渐近线的夹角为,则双曲线的离心率为( )
(2)设F1,F2是双曲线C:(a>0,b>0)的两个焦点,P是C上一点,若6a,且△的最小内角为30°,则双曲线C的离心率为( )
离心率
双曲线的简单几何性质
解: (1)∵a>,∴<1,∴y=x的倾斜角小于45°,
∴=tan=,∴a=,c= =2,
∴e===.(如图所示)
(2)不妨设|PF1|>|PF2|,则|PF1|-|PF2|=2a,又|PF1|+|PF2|=6a,
得|PF1|=4a,|PF2|=2a,|F1F2|=2c,则在△PF1F2中,∠PF1F2=30°,
由余弦定理得(2a)2=(4a)2+(2c)2-2·4a·2c·cos 30°,
整理得(e-)2=0,所以e=.
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
04课堂小结
PART ONE
课堂小结
3.2.2 双曲线的简单几何性质
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
01情景导入
PART ONE
复习导入
复习导入
02双曲线的简单的几何性质
渐近线
PART ONE
双曲线的简单几何性质
y=±2x
求双曲线渐近线
双曲线的简单几何性质
双曲线的简单几何性质
方法总结
双曲线的简单几何性质
AD
双曲线的简单几何性质
双曲线的简单几何性质
C
03双曲线的简单的几何性质
离心率
PART ONE
双曲线的简单几何性质
例2. (1)已知双曲线的两条渐近线的夹角为,则双曲线的离心率为( )
(2)设F1,F2是双曲线C:(a>0,b>0)的两个焦点,P是C上一点,若6a,且△的最小内角为30°,则双曲线C的离心率为( )
离心率
双曲线的简单几何性质
解: (1)∵a>,∴<1,∴y=x的倾斜角小于45°,
∴=tan=,∴a=,c= =2,
∴e===.(如图所示)
(2)不妨设|PF1|>|PF2|,则|PF1|-|PF2|=2a,又|PF1|+|PF2|=6a,
得|PF1|=4a,|PF2|=2a,|F1F2|=2c,则在△PF1F2中,∠PF1F2=30°,
由余弦定理得(2a)2=(4a)2+(2c)2-2·4a·2c·cos 30°,
整理得(e-)2=0,所以e=.
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
04课堂小结
PART ONE
课堂小结
