3.2.1 双曲线及其标准方程(第2课时) 课件(共26张PPT)
文档属性
| 名称 | 3.2.1 双曲线及其标准方程(第2课时) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 40.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 21:06:37 | ||
图片预览








文档简介
(共26张PPT)
3.2.1 双曲线及其标准方程(第2课时)
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.了解双曲线的定义.
2.了解双曲线的几何图形和标准方程.
3.能利用双曲线的定义和待定系数法求双曲线的标准方程.
4.能利用双曲线的标准方程解决实际问题.
01情景导入
PART ONE
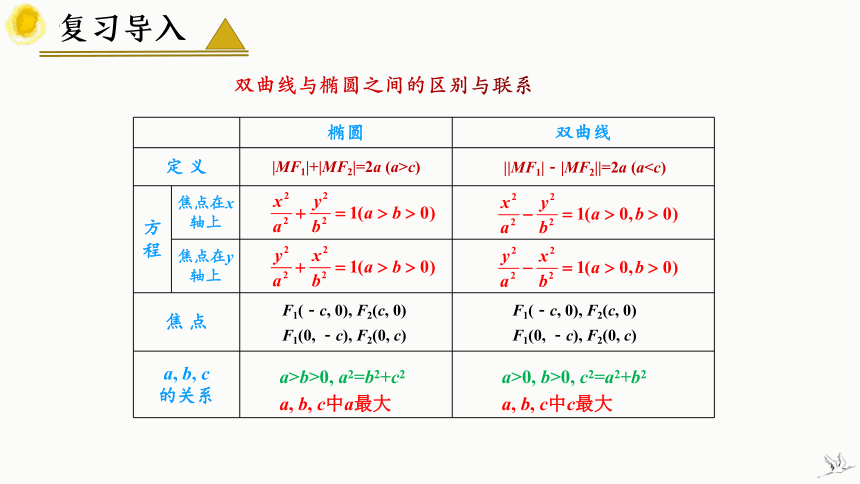
复习导入
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a|MF1|+|MF2|=2a (a>c)
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
02 双曲线焦点三角形
PART ONE
焦点三角形
焦点三角形
例1.设双曲线=1,F1、F2是其两个焦点,点P在双曲线右支上. 若∠F1PF2=90°,
求△F1PF2的面积.
解: 由双曲线方程知a=2,b=3,c=,
设|PF1|=r1,|PF2|=r2(r1>r2),
如图所示.由双曲线定义,有r1-r2=2a=4,
两边平方得+-2r1r2=16.
∵∠F1PF2=90°,
∴+=4c2=4×()2=52.
∴2r1r2=52-16=36,∴S△F1PF2=r1r2=9.
焦点三角形
类题通法
双曲线中的焦点三角形:双曲线上的点P与其两个焦点F1,F2连接而成的三角形PF1F2称为焦点三角形.令|PF1|=r1,|PF2|=r2,∠F1PF2=θ,因|F1F2|=2c,
所以有
(1)定义:|r1-r2|=2a.
(2)余弦定理:4c2=+-2r1r2cos θ.
(3)面积公式:S△PF1F2=r1r2sin θ.
一般地,在△PF1F2中,通过以上三个等式,所求问题就会顺利解决.
焦点三角形
焦点三角形
练习2.已知双曲线 (a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为( )
A.4a B.4a-m
C.4a+2m D.4a-2m
解析:不妨设|AF2|>|AF1|,由双曲线的定义,知|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,
所以|AF2|+|BF2|=(|AF1|+|BF1|)+4a=m+4a,于是△ABF2的周长l=|AF2|+|BF2|+|AB|=4a+2m.故选C.
C
焦点三角形
03 求轨迹方程
PART ONE
轨迹方程
轨迹方程
轨迹方程
[易错防范]
1.求解中易把动点的轨迹看成双曲线,忽视了双曲线定义中“距离的差的绝对值是常数”这一条件,动点轨迹实际上是双曲线的一支.
2.在求解与双曲线有关的轨迹问题时,准确理解双曲线的定义,才能保证解题的正确性.当||PF1|-|PF2||=2a<|F1F2|(a>0),即|PF1|-|PF2|=±2a(0<2a<|F1F2|)时,P点的轨迹是双曲线,其中取正号时为双曲线的右支,取负号时为双曲线的左支.
轨迹方程
例3. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知tan∠PEF= ,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦点且过点P的双曲线方程.
轨迹方程
解:以E,F所在直线为x轴,EF的垂直平分线为y轴建立直角坐标系,如图.
轨迹方程
轨迹方程
【思路分析】 建立坐标系后利用正弦定理与双曲线的定义确定轨迹方程.
轨迹方程
04 求最值
PART ONE
求最值
C
求最值
求最值
求最值
05课堂小结
PART ONE
课堂小结
3.2.1 双曲线及其标准方程(第2课时)
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.了解双曲线的定义.
2.了解双曲线的几何图形和标准方程.
3.能利用双曲线的定义和待定系数法求双曲线的标准方程.
4.能利用双曲线的标准方程解决实际问题.
01情景导入
PART ONE
复习导入
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
02 双曲线焦点三角形
PART ONE
焦点三角形
焦点三角形
例1.设双曲线=1,F1、F2是其两个焦点,点P在双曲线右支上. 若∠F1PF2=90°,
求△F1PF2的面积.
解: 由双曲线方程知a=2,b=3,c=,
设|PF1|=r1,|PF2|=r2(r1>r2),
如图所示.由双曲线定义,有r1-r2=2a=4,
两边平方得+-2r1r2=16.
∵∠F1PF2=90°,
∴+=4c2=4×()2=52.
∴2r1r2=52-16=36,∴S△F1PF2=r1r2=9.
焦点三角形
类题通法
双曲线中的焦点三角形:双曲线上的点P与其两个焦点F1,F2连接而成的三角形PF1F2称为焦点三角形.令|PF1|=r1,|PF2|=r2,∠F1PF2=θ,因|F1F2|=2c,
所以有
(1)定义:|r1-r2|=2a.
(2)余弦定理:4c2=+-2r1r2cos θ.
(3)面积公式:S△PF1F2=r1r2sin θ.
一般地,在△PF1F2中,通过以上三个等式,所求问题就会顺利解决.
焦点三角形
焦点三角形
练习2.已知双曲线 (a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为( )
A.4a B.4a-m
C.4a+2m D.4a-2m
解析:不妨设|AF2|>|AF1|,由双曲线的定义,知|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,
所以|AF2|+|BF2|=(|AF1|+|BF1|)+4a=m+4a,于是△ABF2的周长l=|AF2|+|BF2|+|AB|=4a+2m.故选C.
C
焦点三角形
03 求轨迹方程
PART ONE
轨迹方程
轨迹方程
轨迹方程
[易错防范]
1.求解中易把动点的轨迹看成双曲线,忽视了双曲线定义中“距离的差的绝对值是常数”这一条件,动点轨迹实际上是双曲线的一支.
2.在求解与双曲线有关的轨迹问题时,准确理解双曲线的定义,才能保证解题的正确性.当||PF1|-|PF2||=2a<|F1F2|(a>0),即|PF1|-|PF2|=±2a(0<2a<|F1F2|)时,P点的轨迹是双曲线,其中取正号时为双曲线的右支,取负号时为双曲线的左支.
轨迹方程
例3. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知tan∠PEF= ,tan∠PFE=-2,试建立适当直角坐标系,求出分别以E,F为左、右焦点且过点P的双曲线方程.
轨迹方程
解:以E,F所在直线为x轴,EF的垂直平分线为y轴建立直角坐标系,如图.
轨迹方程
轨迹方程
【思路分析】 建立坐标系后利用正弦定理与双曲线的定义确定轨迹方程.
轨迹方程
04 求最值
PART ONE
求最值
C
求最值
求最值
求最值
05课堂小结
PART ONE
课堂小结
