3.2.2 双曲线的简单几何性质(第1课时) 课件(共32张PPT)
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(第1课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 52.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
3.2.2 双曲线的简单几何性质
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
01情景导入
PART ONE
复习导入
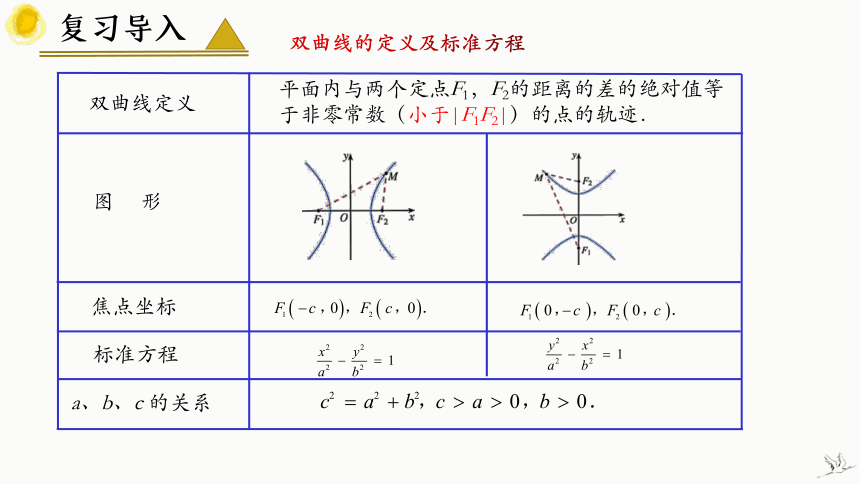
双曲线的定义及标准方程
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
复习导入
观察双曲线的形状,你能从图上看出它的范围吗?它具有怎样的对称性?双曲线上哪些点比较特殊?
观察图,我们发现,不同双曲线的开阔程度不同,你能用适当的量定量刻画双曲线的开阔程度吗?
02双曲线的简单的几何性质
PART ONE
双曲线的简单几何性质
1.范围
类比研究椭圆范围的方法,观察双曲线,我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R .
F1
F2
O
x
y
x=-a
x=a
下面利用双曲线的方程求出它的范围.
这说明双曲线位于直线x=-a及其左侧和直线x=a及其右侧的区域。
双曲线的简单几何性质
2.对称性
类比研究椭圆 对称性的方法,容易得到,双曲线
关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲
线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫做双曲线的中心。
F1
F2
O
x
y
A1(x,y)
A3(-x,y)
A2(x,-y)
A4(-x,-y)
双曲线的简单几何性质
3.顶点
类比椭圆顶点的方法,在方程 中,令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0)和A2(a,0).它们叫做双曲线的顶点.
令x=0,得y2=﹣b2 ,这个方程无解,说明双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
x
O
A1
y
A2
B1
B2
F2
F1
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
实轴与虚轴等长的双曲线叫等轴双曲线
双曲线的简单几何性质
4.渐近线
双曲线的简单几何性质
M(x,y)
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
双曲线的简单几何性质
能不能直接由双曲线方程得出它的渐近线方程?
结论:
(1)双曲线的渐近线方程是即
(2)渐近线方程是的双曲线方程是(λ≠0)
双曲线的简单几何性质
5、离心率
∵c>a>0
∴e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(2)e的范围:
(3)e的含义:
(1)定义:
双曲线的焦距与实轴长的比叫做双曲线的离心率。
x
y
o
a
b
双曲线的简单几何性质
(4)等轴双曲线的离心率e=
( 5 )
A1
A2
B1
B2
a
b
c
x
0
y
几何意义
双曲线的简单几何性质
焦点在y轴上的双曲线的几何性质都有什么?
双曲线标准方程:
双曲线性质:
1、
范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点
B1(0,-a), B2(0,-a)
4、轴:
5、渐近线方程:
6、离心率:
Y
X
A1
A2
B1
B2
F2
F2
o
实轴 B1B2 ; 虚轴 A1A2
探究
双曲线的简单几何性质
双曲线的简单几何性质
03性质简单应用
PART ONE
双曲线的简单几何性质
牛刀小试
|x|≥
6
18
|x|≥3
(±3,0)
y=±3x
4
4
|y|≥2
(0,±2)
10
14
|y|≥5
(0,±5)
双曲线的简单几何性质
例1. 求双曲线9y2 – 16x2 =144的实半轴与虚半轴长,焦点坐标,离心率及渐近线方程, 并画出双曲线草图.
解:
3
-3
4
-4
x
y
O
F1(0,-5)
F2(0,5)
作双曲线草图
双曲线的简单几何性质
(1)由双曲线的方程求几何性质的四个步骤:
(2)画几何图形,要先画双曲线的两条渐近线(即以2a,2b为两邻边的矩形对角线)和两个顶点,然后根据双曲线的变化趋势,就可画出双曲线的大致图形.
方法总结
双曲线的简单几何性质
利用性质求双曲线标准方程
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
方法总结
双曲线的简单几何性质
双曲线的简单几何性质
练习: 根据以下条件,求双曲线的标准方程.
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
04课堂小结
PART ONE
课堂小结
3.2.2 双曲线的简单几何性质
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.理解双曲线的渐近线及离心率的意义.
3.根据几何条件求双曲线的标准方程.
01情景导入
PART ONE
复习导入
双曲线的定义及标准方程
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
复习导入
观察双曲线的形状,你能从图上看出它的范围吗?它具有怎样的对称性?双曲线上哪些点比较特殊?
观察图,我们发现,不同双曲线的开阔程度不同,你能用适当的量定量刻画双曲线的开阔程度吗?
02双曲线的简单的几何性质
PART ONE
双曲线的简单几何性质
1.范围
类比研究椭圆范围的方法,观察双曲线,我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R .
F1
F2
O
x
y
x=-a
x=a
下面利用双曲线的方程求出它的范围.
这说明双曲线位于直线x=-a及其左侧和直线x=a及其右侧的区域。
双曲线的简单几何性质
2.对称性
类比研究椭圆 对称性的方法,容易得到,双曲线
关于x轴、y轴和原点都是对称的.这时,坐标轴是双曲
线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫做双曲线的中心。
F1
F2
O
x
y
A1(x,y)
A3(-x,y)
A2(x,-y)
A4(-x,-y)
双曲线的简单几何性质
3.顶点
类比椭圆顶点的方法,在方程 中,令y=0,得x=±a,因此双曲线和x轴有两个交点A1(-a,0)和A2(a,0).它们叫做双曲线的顶点.
令x=0,得y2=﹣b2 ,这个方程无解,说明双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
x
O
A1
y
A2
B1
B2
F2
F1
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
实轴与虚轴等长的双曲线叫等轴双曲线
双曲线的简单几何性质
4.渐近线
双曲线的简单几何性质
M(x,y)
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的
画出双曲线的草图
(3)
双曲线的简单几何性质
能不能直接由双曲线方程得出它的渐近线方程?
结论:
(1)双曲线的渐近线方程是即
(2)渐近线方程是的双曲线方程是(λ≠0)
双曲线的简单几何性质
5、离心率
∵c>a>0
∴e >1
e是表示双曲线开口大小的一个量,e越大开口越大
(2)e的范围:
(3)e的含义:
(1)定义:
双曲线的焦距与实轴长的比叫做双曲线的离心率。
x
y
o
a
b
双曲线的简单几何性质
(4)等轴双曲线的离心率e=
( 5 )
A1
A2
B1
B2
a
b
c
x
0
y
几何意义
双曲线的简单几何性质
焦点在y轴上的双曲线的几何性质都有什么?
双曲线标准方程:
双曲线性质:
1、
范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点
B1(0,-a), B2(0,-a)
4、轴:
5、渐近线方程:
6、离心率:
Y
X
A1
A2
B1
B2
F2
F2
o
实轴 B1B2 ; 虚轴 A1A2
探究
双曲线的简单几何性质
双曲线的简单几何性质
03性质简单应用
PART ONE
双曲线的简单几何性质
牛刀小试
|x|≥
6
18
|x|≥3
(±3,0)
y=±3x
4
4
|y|≥2
(0,±2)
10
14
|y|≥5
(0,±5)
双曲线的简单几何性质
例1. 求双曲线9y2 – 16x2 =144的实半轴与虚半轴长,焦点坐标,离心率及渐近线方程, 并画出双曲线草图.
解:
3
-3
4
-4
x
y
O
F1(0,-5)
F2(0,5)
作双曲线草图
双曲线的简单几何性质
(1)由双曲线的方程求几何性质的四个步骤:
(2)画几何图形,要先画双曲线的两条渐近线(即以2a,2b为两邻边的矩形对角线)和两个顶点,然后根据双曲线的变化趋势,就可画出双曲线的大致图形.
方法总结
双曲线的简单几何性质
利用性质求双曲线标准方程
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
方法总结
双曲线的简单几何性质
双曲线的简单几何性质
练习: 根据以下条件,求双曲线的标准方程.
双曲线的简单几何性质
双曲线的简单几何性质
双曲线的简单几何性质
04课堂小结
PART ONE
课堂小结
