3.2.2 双曲线的简单几何性质(第3课时)课件(共29张PPT)
文档属性
| 名称 | 3.2.2 双曲线的简单几何性质(第3课时)课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 55.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-08 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
3.2.2 双曲线的简单几何性质
直线与双曲线
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.根据几何条件求双曲线的标准方程.
3.会判断直线与双曲线的位置关系,并解决实际问题.
01情景导入
PART ONE
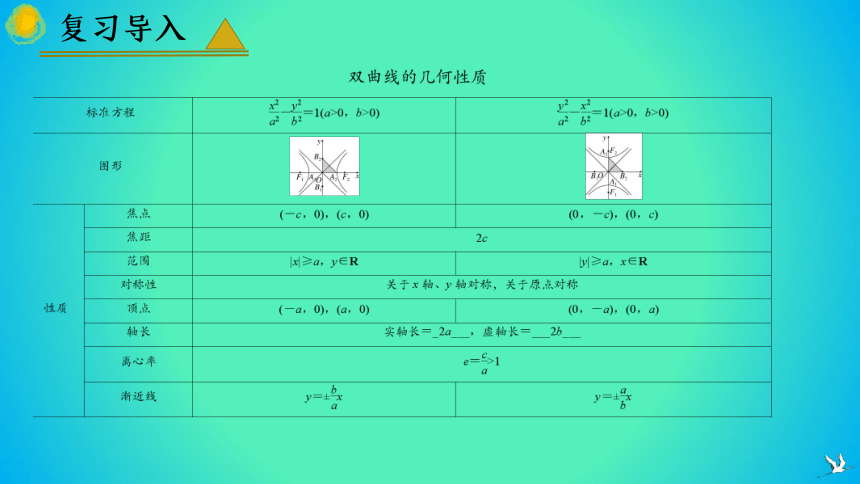
复习导入
02直线与双曲线位置关系
PART ONE
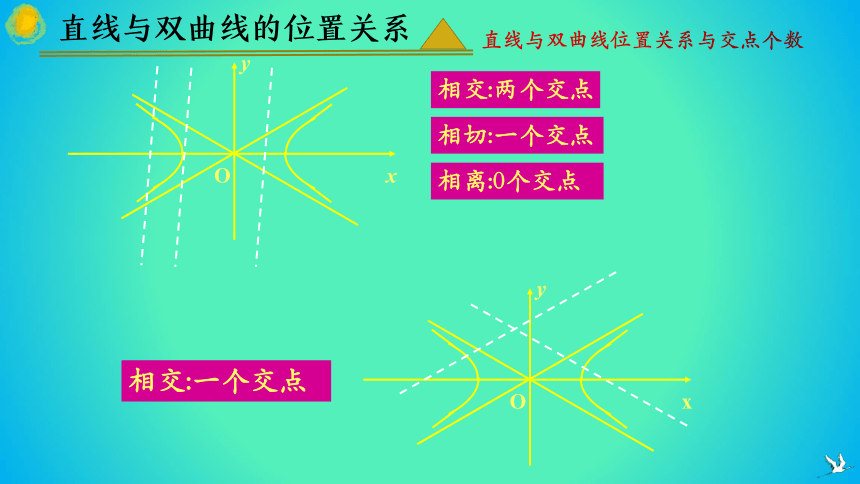
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线位置关系与交点个数
x
y
O
x
y
O
相离:0个交点
相交:一个交点
相交:两个交点
相切:一个交点
直线与双曲线的位置关系
②相切一点: △=0
③相 离: △<0
①直线与双曲线相交两点: △>0
同侧:x1x2>0
异侧: x1x2<0
直线与双曲线相交一点: 直线与渐进线平行
特别注意:直线与双曲线的位置关系中:一解不一定相切,相交不一定两解,两解不一定同支
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线的位置关系
练习1. 已知双曲线C:-=1(a>0,b>0)的离心率为,且过点P(,1).
(1)求双曲线C的方程;
(2)若直线l1:y=kx+与双曲线C恒有两个不同的交点A,B,求k的取值范围.
解: (1)由e=,可得a2=3b2,故双曲线方程可化为-=1.
将点P(,1)代入双曲线C的方程,可解得b2=1.所以双曲线C的方程为-=1.
(2)联立直线与双曲线方程 (1-3k2)x2-6kx-9=0,由题意得解得-1<k<1且k≠±,
所以k的取值范围为-1<k<1且k≠±.
直线与双曲线的位置关系
x
y
O
练习2:过点P(1,1)与双曲线
只有一个交点的直线有( )条
4
(1,1)
变题:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).
答案又是怎样的
答案:1.两条;
2.三条;
3.两条;
4.零条.
直线与双曲线的位置关系
直线与双曲线的位置关系
03弦长、中点弦问题
PART ONE
弦长、中点弦问题
弦长、中点弦问题
弦长、中点弦问题
弦长、中点弦问题
例3. 经过点M(2,2)作直线l交双曲线-=1于A,B两点,且M为AB中点.
(1)求直线l的方程;
(2)求线段AB的长.
解:(1)设A(x1,y1),B(x2,y2),代入双曲线方程得-=1,
两式相减得--(-)=0,(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0.
∵M为AB的中点,∴x1+x2=4,y1+y2=4,∴4(x1-x2)-(y1-y2)=0,kl==4,
经检验k=4符合题意.∴l的方程为y-2=4(x-2),即y=4x-6.
(2)将y=4x-6代入到-=1中得3x2-12x+10=0,故x1+x2=4,x1x2=,
∴|AB|==.
弦长、中点弦问题
B
弦长、中点弦问题
弦长、中点弦问题
练习 2:已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
解: 法一:由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),即y=kx-3k-1,
由消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),∴x1+x2=.
∵A(3,-1)为MN的中点,∴=3,即=3,解得k=-.
当k=-时,满足Δ>0,符合题意,
∴所求直线MN的方程为y=-x+,即3x+4y-5=0.
法二:设M(x1,y1),N(x2,y2),∵M,N均在双曲线上,∴-y12=1,-y22=1 ,
两式相减得=.∵点A平分弦MN,∴x1+x2=6,y1+y2=-2. ∴kMN==-.
经验证,该直线MN存在.∴所求直线MN的方程为y+1=-(x-3),即3x+4y-5=0.
04求轨迹方程
PART ONE
轨迹方程
例4
解:由题意可得
轨迹方程
例5 .双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
轨迹方程
05课堂小结
PART ONE
课堂小结
3.2.2 双曲线的简单几何性质
直线与双曲线
第 三 章 圆锥曲线的方程
人教A版2019选修第一册
学习目标
1.掌握双曲线的简单几何性质.
2.根据几何条件求双曲线的标准方程.
3.会判断直线与双曲线的位置关系,并解决实际问题.
01情景导入
PART ONE
复习导入
02直线与双曲线位置关系
PART ONE
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线位置关系与交点个数
x
y
O
x
y
O
相离:0个交点
相交:一个交点
相交:两个交点
相切:一个交点
直线与双曲线的位置关系
②相切一点: △=0
③相 离: △<0
①直线与双曲线相交两点: △>0
同侧:x1x2>0
异侧: x1x2<0
直线与双曲线相交一点: 直线与渐进线平行
特别注意:直线与双曲线的位置关系中:一解不一定相切,相交不一定两解,两解不一定同支
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线的位置关系
直线与双曲线的位置关系
练习1. 已知双曲线C:-=1(a>0,b>0)的离心率为,且过点P(,1).
(1)求双曲线C的方程;
(2)若直线l1:y=kx+与双曲线C恒有两个不同的交点A,B,求k的取值范围.
解: (1)由e=,可得a2=3b2,故双曲线方程可化为-=1.
将点P(,1)代入双曲线C的方程,可解得b2=1.所以双曲线C的方程为-=1.
(2)联立直线与双曲线方程 (1-3k2)x2-6kx-9=0,由题意得解得-1<k<1且k≠±,
所以k的取值范围为-1<k<1且k≠±.
直线与双曲线的位置关系
x
y
O
练习2:过点P(1,1)与双曲线
只有一个交点的直线有( )条
4
(1,1)
变题:将点P(1,1)改为
1.A(3,4)
2.B(3,0)
3.C(4,0)
4.D(0,0).
答案又是怎样的
答案:1.两条;
2.三条;
3.两条;
4.零条.
直线与双曲线的位置关系
直线与双曲线的位置关系
03弦长、中点弦问题
PART ONE
弦长、中点弦问题
弦长、中点弦问题
弦长、中点弦问题
弦长、中点弦问题
例3. 经过点M(2,2)作直线l交双曲线-=1于A,B两点,且M为AB中点.
(1)求直线l的方程;
(2)求线段AB的长.
解:(1)设A(x1,y1),B(x2,y2),代入双曲线方程得-=1,
两式相减得--(-)=0,(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0.
∵M为AB的中点,∴x1+x2=4,y1+y2=4,∴4(x1-x2)-(y1-y2)=0,kl==4,
经检验k=4符合题意.∴l的方程为y-2=4(x-2),即y=4x-6.
(2)将y=4x-6代入到-=1中得3x2-12x+10=0,故x1+x2=4,x1x2=,
∴|AB|==.
弦长、中点弦问题
B
弦长、中点弦问题
弦长、中点弦问题
练习 2:已知双曲线-y2=1,求过点A (3,-1)且被点A平分的弦MN所在直线的方程.
解: 法一:由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),即y=kx-3k-1,
由消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),∴x1+x2=.
∵A(3,-1)为MN的中点,∴=3,即=3,解得k=-.
当k=-时,满足Δ>0,符合题意,
∴所求直线MN的方程为y=-x+,即3x+4y-5=0.
法二:设M(x1,y1),N(x2,y2),∵M,N均在双曲线上,∴-y12=1,-y22=1 ,
两式相减得=.∵点A平分弦MN,∴x1+x2=6,y1+y2=-2. ∴kMN==-.
经验证,该直线MN存在.∴所求直线MN的方程为y+1=-(x-3),即3x+4y-5=0.
04求轨迹方程
PART ONE
轨迹方程
例4
解:由题意可得
轨迹方程
例5 .双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面.它的最小半径为12m,上口半径为13m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
轨迹方程
05课堂小结
PART ONE
课堂小结
