13.2探索直角三角形全等的条件(广东省汕头市澄海区)
文档属性
| 名称 | 13.2探索直角三角形全等的条件(广东省汕头市澄海区) |  | |
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-12 21:39:00 | ||
图片预览



文档简介
课件27张PPT。授课教师:曾楚璧
2007.11.20 13.2探索直角三角形全等的条件 (H L)旧知回顾判断两个三角形全等的方法
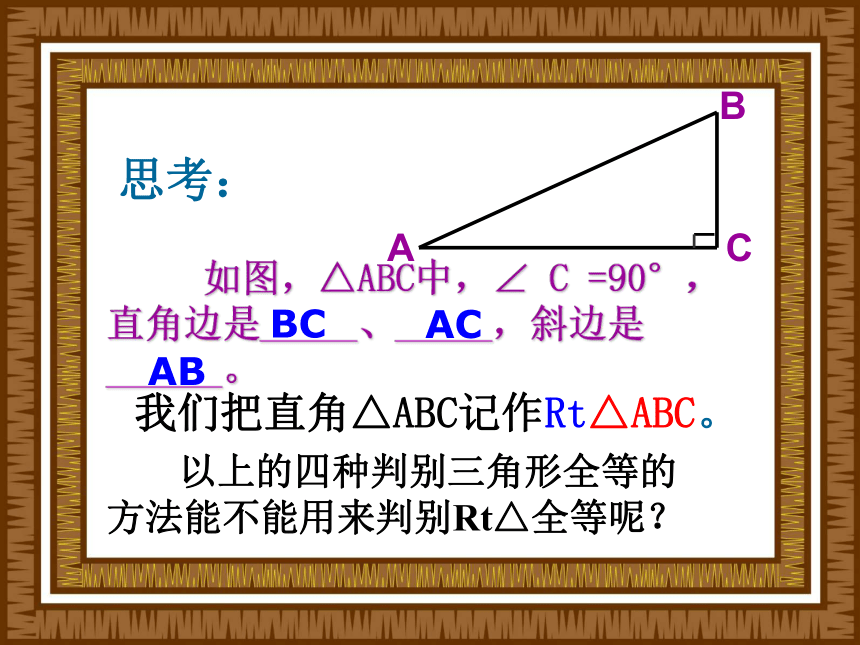
我们已经学了哪些呢?SSSSASASAAAS 三边对应相等的两个三角形全等。(简写成边 边 边“边边边”或“SSS”)边 角 边“边角边”或“SAS”) 两边和它们夹角对应相等的两个三角形全等。(简写成角 边 角“角边角”或“ASA”) 两角和它们的夹边对应相等的两个三角形全等。(简写成角 角 边 两个角和其中一个角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”) 如图,△ABC中,∠ C =90°,直角边是_____、_____,斜边是______。我们把直角△ABC记作Rt△ABC。ACBCAB 以上的四种判别三角形全等的
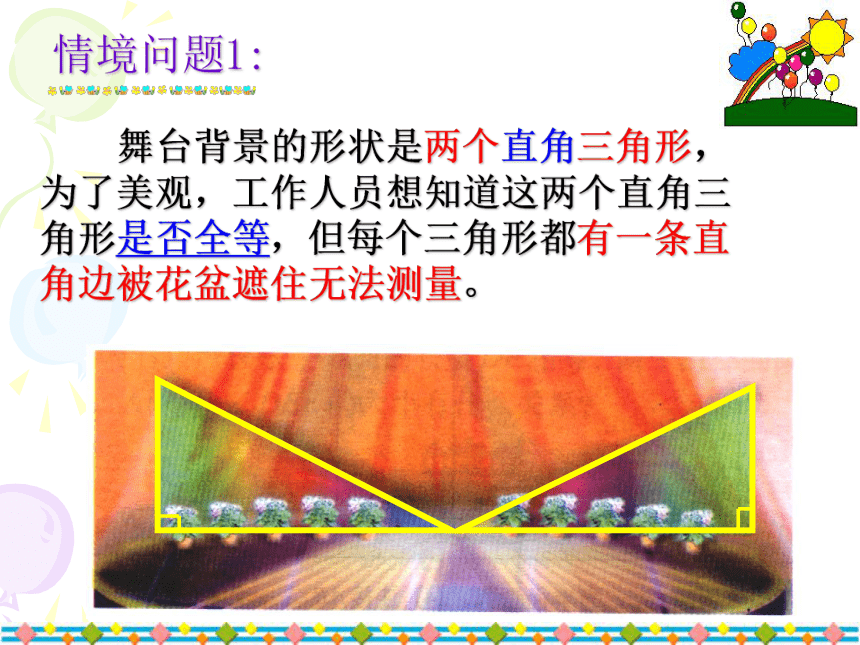
方法能不能用来判别Rt△全等呢?思考: 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。你能帮工作人员想个办法吗?∠B=∠F=Rt ∠ 则利用 可判定全等; ①若测得AB=DF,∠A=∠D, 则利用 可判定全等; A SA②若测得AB=DF,∠C=∠E, A AS③若测得AC=DE,∠C=∠E, 则利用 可判定全等; A AS④若测得AC=DE,∠A=∠D, 则利用 可判定全等; A AS⑤若测得AC=DE,∠A=∠D,AB=DE, 则利用 可判定全等; S AS 如果工作人员只带了一条尺,能完成这项任务吗? 工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗? 对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗? 任意画出一个Rt△ABC,∠C=90°。B′A′按照下面的步骤画Rt△A′B′C′⑴ 作∠MC′N=90°;⑵ 在射线C′M上取段B′C′=BC;⑶ 以B′为圆心,AB为半径画弧,交
射线C′N于点A′;⑷ 连接A′B′.再画一个Rt△A′B′C′,使得∠C′= 90°, B′C′=BC,A′B′= AB。 把你所画的三角形撕出来,与原三角形进行比较,看是否能重合?亲 自 实 践 任意画出一个Rt△ABC,∠C=90°。再画一个Rt△A′B′C′,使得∠C′= 90°, B′C′=BC,A′B′= AB。B′A′按照下面的步骤画一画⑴ 作∠MC′N=90°;⑵ 在射线C′M上取段B′C′=BC;⑶ 以B′为圆心,AB为半径画弧,交
射线C′N于点A′;⑷ 连接A′B′.现象:两个直角三角形能重合。说明:当一个直角三角形的一条直角边和
斜边确定后,那么它的形状和大小也被确定.探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt△A′B′C′中(HL)BC=B′C′ 通过刚才的探索,发现工作人员的做法是完全正确的。(1)如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD∴BC=AD新知应用:(HL)(全等三角形对应边相等) (2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?课本103页练习CD 与CE 相等吗?(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
判断两个直角三角形全等的方法有:(1): ;(2): ;(3): ;(4): ;SSSSASASAAAS(5): ;HL 小结 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1) ( )
(2) ( )
(3) ( )
(4) ( )
练一练AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS作 业:P104 第7、8题
课外练习:1、每个同学完成《基础与提高》
P31页第1、3、4题
2、要竞赛的同学再完成《基础与提高》
P31页第5、6题
作业与练习作 业:P104 第7、8题
课外练习:1、每个同学完成《基础与提高》
P31页第1、2、3、4题
2、要竞赛的同学再完成《基础与提高》
P31页第5、6题
作业与练习证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(全等三角形对应边相等)(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
2007.11.20 13.2探索直角三角形全等的条件 (H L)旧知回顾判断两个三角形全等的方法
我们已经学了哪些呢?SSSSASASAAAS 三边对应相等的两个三角形全等。(简写成边 边 边“边边边”或“SSS”)边 角 边“边角边”或“SAS”) 两边和它们夹角对应相等的两个三角形全等。(简写成角 边 角“角边角”或“ASA”) 两角和它们的夹边对应相等的两个三角形全等。(简写成角 角 边 两个角和其中一个角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”) 如图,△ABC中,∠ C =90°,直角边是_____、_____,斜边是______。我们把直角△ABC记作Rt△ABC。ACBCAB 以上的四种判别三角形全等的
方法能不能用来判别Rt△全等呢?思考: 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。你能帮工作人员想个办法吗?∠B=∠F=Rt ∠ 则利用 可判定全等; ①若测得AB=DF,∠A=∠D, 则利用 可判定全等; A SA②若测得AB=DF,∠C=∠E, A AS③若测得AC=DE,∠C=∠E, 则利用 可判定全等; A AS④若测得AC=DE,∠A=∠D, 则利用 可判定全等; A AS⑤若测得AC=DE,∠A=∠D,AB=DE, 则利用 可判定全等; S AS 如果工作人员只带了一条尺,能完成这项任务吗? 工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗? 对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗? 任意画出一个Rt△ABC,∠C=90°。B′A′按照下面的步骤画Rt△A′B′C′⑴ 作∠MC′N=90°;⑵ 在射线C′M上取段B′C′=BC;⑶ 以B′为圆心,AB为半径画弧,交
射线C′N于点A′;⑷ 连接A′B′.再画一个Rt△A′B′C′,使得∠C′= 90°, B′C′=BC,A′B′= AB。 把你所画的三角形撕出来,与原三角形进行比较,看是否能重合?亲 自 实 践 任意画出一个Rt△ABC,∠C=90°。再画一个Rt△A′B′C′,使得∠C′= 90°, B′C′=BC,A′B′= AB。B′A′按照下面的步骤画一画⑴ 作∠MC′N=90°;⑵ 在射线C′M上取段B′C′=BC;⑶ 以B′为圆心,AB为半径画弧,交
射线C′N于点A′;⑷ 连接A′B′.现象:两个直角三角形能重合。说明:当一个直角三角形的一条直角边和
斜边确定后,那么它的形状和大小也被确定.探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt△A′B′C′中(HL)BC=B′C′ 通过刚才的探索,发现工作人员的做法是完全正确的。(1)如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD∴BC=AD新知应用:(HL)(全等三角形对应边相等) (2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?课本103页练习CD 与CE 相等吗?(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
判断两个直角三角形全等的方法有:(1): ;(2): ;(3): ;(4): ;SSSSASASAAAS(5): ;HL 小结 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由。
(1) ( )
(2) ( )
(3) ( )
(4) ( )
练一练AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS作 业:P104 第7、8题
课外练习:1、每个同学完成《基础与提高》
P31页第1、3、4题
2、要竞赛的同学再完成《基础与提高》
P31页第5、6题
作业与练习作 业:P104 第7、8题
课外练习:1、每个同学完成《基础与提高》
P31页第1、2、3、4题
2、要竞赛的同学再完成《基础与提高》
P31页第5、6题
作业与练习证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(全等三角形对应边相等)(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
