5.1 二次函数 课件(共22张PPT)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 5.1 二次函数 课件(共22张PPT)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 06:38:57 | ||
图片预览








文档简介
(共22张PPT)
5.1 二次函数
第5章 二次函数
教学目标
01
探索自然界中的抛物线,并能根据实际问题抽象出二次函数
02
理解二次函数的概念,熟悉其一般形式,并能准确、快速地识别出二次函数
公元前4世纪,希腊数学家梅里克缪斯在研究日晷时发现:圆锥不仅可以切出一个圆、一个椭圆,还可以切出一个优美的未知图形
横切 斜切 竖切
这个图形下究竟隐藏的是怎样一条曲线呢?
01
情境引入Part1
中世纪,意大利物理学家伽利略发现:把物体斜着抛出去后,其运动的轨迹正是这条曲线,而且还是自然界中物体普遍的运动轨迹,即抛物线。
01
情境引入Part1
现在就让我们一起来揭开抛物线神秘的面纱~
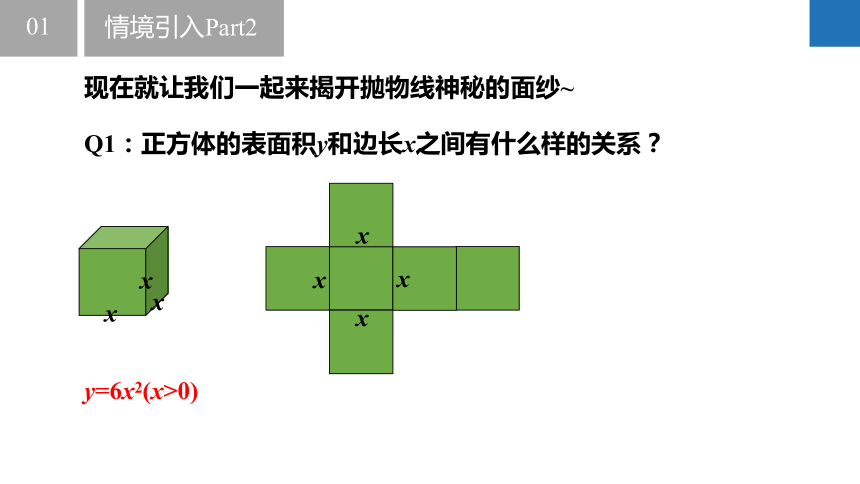
Q1:正方体的表面积y和边长x之间有什么样的关系?
y=6x2(x>0)
x
x
x
x
x
x
x
01
情境引入Part2
Q2:n个球队比赛,每两个球队之间进行一场比赛,比赛的场次数m和球队数n之间有什么关系?
m=[(n-1)+(n-1)+…+(n-1)]=n(n-1)=n2-n
n个(n-1)
01
情境引入Part2
Q3:某种产品现在的年产量是20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划的所定的x的值而确定,y与x之间的关系应怎样表示?
y=20(1+x)2=20x2+40x+20
01
情境引入Part2
观察下列三个函数式,找出它们的共同点:
02
知识精讲
y=6x2
m=n2-n
y=20x2+40x+20
函数式左边是因变量,右边是关于自变量的整式;
且自变量的最高次数是2。
二次函数
其图像即抛物线
二次函数的定义
注意:(1)通常,自变量x是任意实数;
(2)实际问题中,要注意自变量x的取值范围,
eg:y=6x2,x>0。
定义:一般地,形如y=ax2+bx+c(a、b、c是常数,且a≠0)的函数,叫做二次函数,其中x是自变量,y是因变量。
02
知识精讲
二次函数的一般形式
一般形式:
一般地,任何一个关于x的二次函数经过整理,都能化成形如y=ax2+bx+c(a≠0)的形式,其中ax2是二次项,a是二次项系数,bx是一次项,b为一次项系数,c是常数项。
02
知识精讲
注意:要确定二次项系数、一次项系数和常数项,必须先把二次函数化成一般形式。
二次函数的概念
02
知识精讲
二次函数的三要素
三要素:
(1)ax2+bx+c是整式;
(2)自变量x的最高次数是2;
(3)a≠0。
Q1:y=x2++520是二次函数吗?
不是,是分式,不是整式
Q2:y=0x2+1314x+520是二次函数吗?
02
知识精讲
不是,y=0x2+1314x+520=1314x+520,是一次函数
Q3:y=(m-1)x2+1314x+520是二次函数吗?
不一定,需要分类讨论
02
知识精讲
(1)若m-1=0,即m=1,则y=1314x+520,是一次函数
(2)若m-1≠0,即m≠1,符合“a≠0”的要求,是二次函数
02
知识精讲
二次函数
完成下列表格:
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0
二次函数 a≠0 b=c=0
b≠0,c=0
b=0,c≠0
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0 y=bx+c
二次函数 a≠0 b=c=0 y=ax2
b≠0,c=0 y=ax2+bx
b=0,c≠0 y=ax2+c
例1、下列选项描述的y与x之间的关系是二次函数的是( )
A.正方体的体积y与棱长x之间的关系
B.某商品在6月的售价为30元,7月和8月连续两次降价销售,平均每月降价的百分率为x,该商品8月的售价y与x之间的关系
C.距离一定时,汽车匀速行驶的时间y与速度x之间的关系
D.等腰三角形的顶角度数y与底角度数x之间的关系
B
03
典例精析
【分析】A.y=x3,是三次函数;
B.y=30(1-x)2,是二次函数;
C.y=,是反比例函数;
D.y=180°-2x,是一次函数。
例2、下列二次函数中,二次项系数、一次项系数和常数项分别是1,-1,0的是( )
A.y=(x-2)(x+1)
B.y=(x-1)2-2x2-1
C.y=(x+2)(x-3)+6
D. y=(2x-1)2-3(x2-x)
A.y=x2-x-2——1,-1,-2 ×
B.y=-x2-2x——-1,-2,0 ×
C.y=x2-x——1,-1,0 √
D.y=x2-x+1——1,-1,1 ×
C
03
典例精析
例3、下列各式中,一定是二次函数的有( )
(1)y=2x2-4x+3;(2)y=4x3-3x+7;(3)y=(2x-3)(3x-2)-6;
(4)y=x2-3x+5;(5)y=ax2+bx+c(a、b、c为常数);
(6)y=(m2+1)x2-2x-3(m为常数);(7)y=m2+4x-3(m为常数)
A. 2个 B. 3个 C. 4个 D. 5个
【分析】(1)√;(2)是三次函数,×;(3)整理得:y=6x2-13x,√;
(4)√;(5) a≠0时,才是二次函数,×;
(6) m2+1>0,√;(7) 整理得:y=4x+(m2-3),是一次函数,×。
C
03
典例精析
例4、(1)若y=(2-m)x2+m2-2是二次函数,则m不等于( )
A.±2
B.2
C.-2
D.不能确定
【分析】2-m≠0,即m≠2
B
03
典例精析
例4、(2)当m=_____时,y=(m-1)x+1+(m+1)x+2是关于x的二次函数。
-1
注意:
m-1≠0千万不能忘
【分析】由题意可得:
,即
03
典例精析
例4、(3)m满足什么条件时,y=m2(x2+2x)-(2m+3)x2+(x+1)是关于x的二次函数
解:y=m2(x2+2x)-(2m+3)x2+(x+1)
=m2x2+2m2x-2mx2-3x2+x+1
=(m2-2m-3)x2+(2m2+1)x+1,
由题意可得:m2-2m-3≠0,
即(m+1)(m-3)≠0,
∴m≠-1且m≠3。
03
典例精析
课后总结
定义:一般地,形如y=ax2+bx+c(a、b、c是常数,且a≠0)的函数,叫做二次函数,其中x是自变量,y是因变量。
注意:(1)通常,自变量x是任意实数;
(2)实际问题中,要注意自变量x的取值范围,
eg:y=6x2,x>0。
一般形式:
一般地,任何一个关于x的二次函数经过整理,都能化成形如y=ax2+bx+c(a≠0)的形式,其中ax2是二次项,a是二次项系数,bx是一次项,b为一次项系数,c是常数项。
注意:要确定二次项系数,一次项系数和常数项,必须先把二次函数化成一般形式。
课后总结
三要素:
(1)ax2+bx+c是整式;
(2)自变量x的最高次数是2;
(3)a≠0。
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0 y=bx+c
二次函数 a≠0 b=c=0 y=ax2
b≠0,c=0 y=ax2+bx
b=0,c≠0 y=ax2+c
5.1 二次函数
第5章 二次函数
教学目标
01
探索自然界中的抛物线,并能根据实际问题抽象出二次函数
02
理解二次函数的概念,熟悉其一般形式,并能准确、快速地识别出二次函数
公元前4世纪,希腊数学家梅里克缪斯在研究日晷时发现:圆锥不仅可以切出一个圆、一个椭圆,还可以切出一个优美的未知图形
横切 斜切 竖切
这个图形下究竟隐藏的是怎样一条曲线呢?
01
情境引入Part1
中世纪,意大利物理学家伽利略发现:把物体斜着抛出去后,其运动的轨迹正是这条曲线,而且还是自然界中物体普遍的运动轨迹,即抛物线。
01
情境引入Part1
现在就让我们一起来揭开抛物线神秘的面纱~
Q1:正方体的表面积y和边长x之间有什么样的关系?
y=6x2(x>0)
x
x
x
x
x
x
x
01
情境引入Part2
Q2:n个球队比赛,每两个球队之间进行一场比赛,比赛的场次数m和球队数n之间有什么关系?
m=[(n-1)+(n-1)+…+(n-1)]=n(n-1)=n2-n
n个(n-1)
01
情境引入Part2
Q3:某种产品现在的年产量是20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划的所定的x的值而确定,y与x之间的关系应怎样表示?
y=20(1+x)2=20x2+40x+20
01
情境引入Part2
观察下列三个函数式,找出它们的共同点:
02
知识精讲
y=6x2
m=n2-n
y=20x2+40x+20
函数式左边是因变量,右边是关于自变量的整式;
且自变量的最高次数是2。
二次函数
其图像即抛物线
二次函数的定义
注意:(1)通常,自变量x是任意实数;
(2)实际问题中,要注意自变量x的取值范围,
eg:y=6x2,x>0。
定义:一般地,形如y=ax2+bx+c(a、b、c是常数,且a≠0)的函数,叫做二次函数,其中x是自变量,y是因变量。
02
知识精讲
二次函数的一般形式
一般形式:
一般地,任何一个关于x的二次函数经过整理,都能化成形如y=ax2+bx+c(a≠0)的形式,其中ax2是二次项,a是二次项系数,bx是一次项,b为一次项系数,c是常数项。
02
知识精讲
注意:要确定二次项系数、一次项系数和常数项,必须先把二次函数化成一般形式。
二次函数的概念
02
知识精讲
二次函数的三要素
三要素:
(1)ax2+bx+c是整式;
(2)自变量x的最高次数是2;
(3)a≠0。
Q1:y=x2++520是二次函数吗?
不是,是分式,不是整式
Q2:y=0x2+1314x+520是二次函数吗?
02
知识精讲
不是,y=0x2+1314x+520=1314x+520,是一次函数
Q3:y=(m-1)x2+1314x+520是二次函数吗?
不一定,需要分类讨论
02
知识精讲
(1)若m-1=0,即m=1,则y=1314x+520,是一次函数
(2)若m-1≠0,即m≠1,符合“a≠0”的要求,是二次函数
02
知识精讲
二次函数
完成下列表格:
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0
二次函数 a≠0 b=c=0
b≠0,c=0
b=0,c≠0
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0 y=bx+c
二次函数 a≠0 b=c=0 y=ax2
b≠0,c=0 y=ax2+bx
b=0,c≠0 y=ax2+c
例1、下列选项描述的y与x之间的关系是二次函数的是( )
A.正方体的体积y与棱长x之间的关系
B.某商品在6月的售价为30元,7月和8月连续两次降价销售,平均每月降价的百分率为x,该商品8月的售价y与x之间的关系
C.距离一定时,汽车匀速行驶的时间y与速度x之间的关系
D.等腰三角形的顶角度数y与底角度数x之间的关系
B
03
典例精析
【分析】A.y=x3,是三次函数;
B.y=30(1-x)2,是二次函数;
C.y=,是反比例函数;
D.y=180°-2x,是一次函数。
例2、下列二次函数中,二次项系数、一次项系数和常数项分别是1,-1,0的是( )
A.y=(x-2)(x+1)
B.y=(x-1)2-2x2-1
C.y=(x+2)(x-3)+6
D. y=(2x-1)2-3(x2-x)
A.y=x2-x-2——1,-1,-2 ×
B.y=-x2-2x——-1,-2,0 ×
C.y=x2-x——1,-1,0 √
D.y=x2-x+1——1,-1,1 ×
C
03
典例精析
例3、下列各式中,一定是二次函数的有( )
(1)y=2x2-4x+3;(2)y=4x3-3x+7;(3)y=(2x-3)(3x-2)-6;
(4)y=x2-3x+5;(5)y=ax2+bx+c(a、b、c为常数);
(6)y=(m2+1)x2-2x-3(m为常数);(7)y=m2+4x-3(m为常数)
A. 2个 B. 3个 C. 4个 D. 5个
【分析】(1)√;(2)是三次函数,×;(3)整理得:y=6x2-13x,√;
(4)√;(5) a≠0时,才是二次函数,×;
(6) m2+1>0,√;(7) 整理得:y=4x+(m2-3),是一次函数,×。
C
03
典例精析
例4、(1)若y=(2-m)x2+m2-2是二次函数,则m不等于( )
A.±2
B.2
C.-2
D.不能确定
【分析】2-m≠0,即m≠2
B
03
典例精析
例4、(2)当m=_____时,y=(m-1)x+1+(m+1)x+2是关于x的二次函数。
-1
注意:
m-1≠0千万不能忘
【分析】由题意可得:
,即
03
典例精析
例4、(3)m满足什么条件时,y=m2(x2+2x)-(2m+3)x2+(x+1)是关于x的二次函数
解:y=m2(x2+2x)-(2m+3)x2+(x+1)
=m2x2+2m2x-2mx2-3x2+x+1
=(m2-2m-3)x2+(2m2+1)x+1,
由题意可得:m2-2m-3≠0,
即(m+1)(m-3)≠0,
∴m≠-1且m≠3。
03
典例精析
课后总结
定义:一般地,形如y=ax2+bx+c(a、b、c是常数,且a≠0)的函数,叫做二次函数,其中x是自变量,y是因变量。
注意:(1)通常,自变量x是任意实数;
(2)实际问题中,要注意自变量x的取值范围,
eg:y=6x2,x>0。
一般形式:
一般地,任何一个关于x的二次函数经过整理,都能化成形如y=ax2+bx+c(a≠0)的形式,其中ax2是二次项,a是二次项系数,bx是一次项,b为一次项系数,c是常数项。
注意:要确定二次项系数,一次项系数和常数项,必须先把二次函数化成一般形式。
课后总结
三要素:
(1)ax2+bx+c是整式;
(2)自变量x的最高次数是2;
(3)a≠0。
y=ax2+bx+c 函数类型 参数取值 函数表达式
一次函数 a=0 y=bx+c
二次函数 a≠0 b=c=0 y=ax2
b≠0,c=0 y=ax2+bx
b=0,c≠0 y=ax2+c
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
