18.3反比例函数的图像和性质(第2课时)课件(共36张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 18.3反比例函数的图像和性质(第2课时)课件(共36张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览









文档简介
沪教版八年级上册
第18章 正比例函数与反比例函数
18.3反比例函数的图像和性质(第2课时)
1.经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程 (重点、难点)
2.会画反比例函数图象,了解和掌握反比例函数的图象和性质.(重点)
学习目标
2、其定义域是什么?
复习引入
1、什么是反比例函数?
形如_____________________是反比例函数.
不等于零的一切实数
今天学习反比例函数的图像与性质
(即 )
操作1:画反比例函数 的图像
画反比例函数的图像
画函数图象有哪些步骤?
列表、描点、连线
自变量x的取值范围是什么?
通常在0的附近,正数和负数至少各取5个数
自变量x取哪些数比较容易计算出y的值呢?
操作1:画反比例函数 的图像
把各点用光滑的曲线连接,再向两方伸展
第一象限和第三象限各有一支曲线
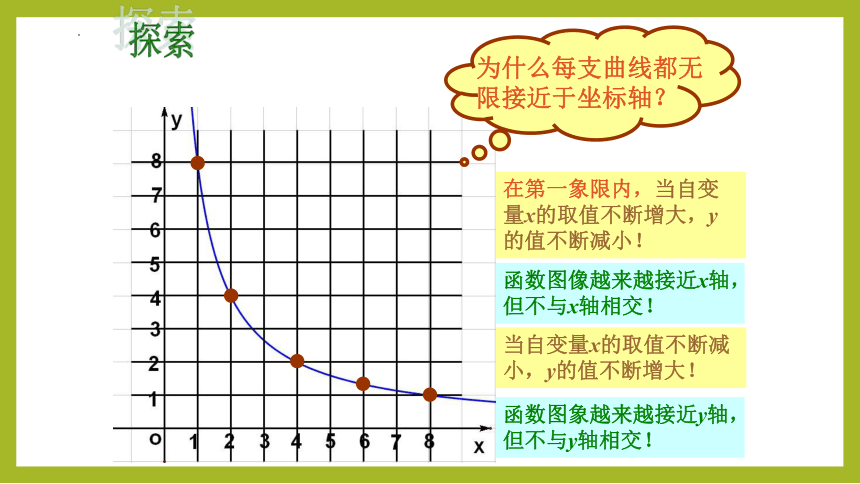
探索
两支曲线,分别在第一、三象限.
反比例函数 的图像与正比例函数有何区别?
图像不会与坐标轴相交,
即图像向两方无限延伸.
图像是否会与坐标轴相交?为什么?
探索
在第一象限内,当自变量x的取值不断增大,y的值不断减小!
当自变量x的取值不断减小,y的值不断增大!
函数图像越来越接近x轴,但不与x轴相交!
函数图象越来越接近y轴,但不与y轴相交!
为什么每支曲线都无限接近于坐标轴?
操作2:画反比例函数 的图像
同样是两支曲线!
两支曲线在第二、四象限!
函数图像不会与坐标轴相交,即图像向两方无限延伸.
反比例函数 图像和 有何相同和区别?
图像是否会与坐标轴相交?
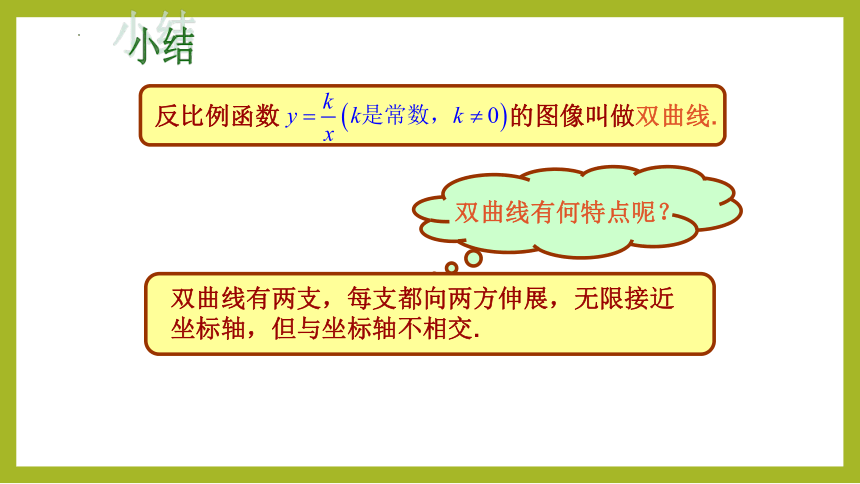
反比例函数 的图像叫做双曲线.
小结
双曲线有何特点呢?
双曲线有两支,每支都向两方伸展,无限接近坐标轴,但与坐标轴不相交.
操作3:(1)画反比例函数 和 的图像
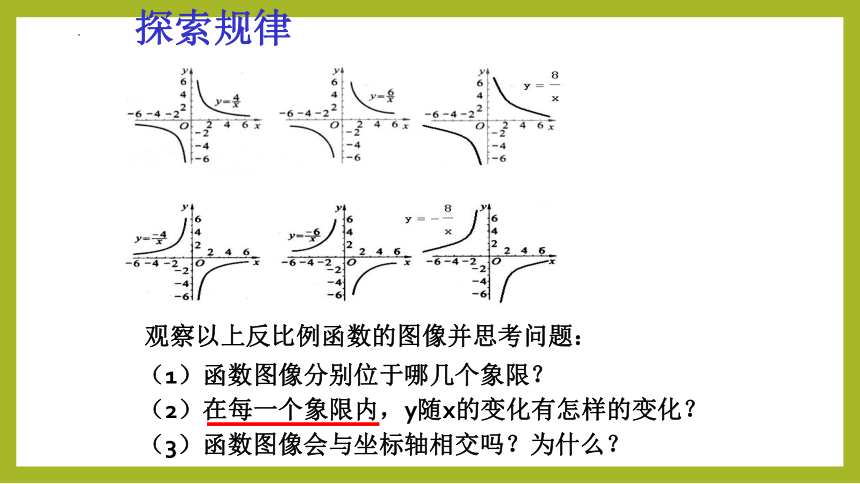
探索规律
观察以上反比例函数的图像并思考问题:
(1)函数图像分别位于哪几个象限?
(2)在每一个象限内,y随x的变化有怎样的变化?
(3)函数图像会与坐标轴相交吗?为什么?
一般地,反比例函数 y= ( k为常数, k≠0 )的图像是双曲线,它具有以下性质:
反比例函数的性质
(1)当k>0时,函数图像的两支分别在第一、三象限,在每一
个象限内,当自变量x的值逐渐增大时,y的值随着逐渐减小。
(2)当k<0时,函数图像的两支分别在第二、四象限,在每一
个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大。
(3)图像的两支都无限接近于x轴和y轴,但不会与x轴和y轴相交。
2010年世博会在上海召开,设计专家计划在园区内一块休息区域种植8km2 的植被,如果按长方形种植,它们的长与宽分别如下图:这些长方形的长与宽有什么关系?
8
1
2
1
2
8
单位:km
4
4
x
y
o
1
8
2
4
4
2
8
1
A1
A2
A3
A4
讨论1:请你说出A1、A2、A3、A4四个点的
纵坐标y和横坐标x满足怎样的函数关系?
(1,8)
(2,4)
(4,2)
(8,1)
设点P(m,n)是该函数图象上任意一点,过P分别作x轴y轴的垂线段,垂足为A、B,构成的长方形面积是多少?
P(m,n)
A
B
1.画反比例函数 和 的图像
课本练习
在其图像所在的每个象限内,y的值随x的值的增大而
减小的函数是________________.
其中,图像位于第二、四象限的函数是
_________________________________;
3、已知下列反比例函数:
4.如果反比例函数 ( 是常数,
),的图像在第二、四象限,那么正
比例函数 ( 是常数, )的
图像经过哪几个象限?
1. 反比例函数 的图象大致是 ( )
C
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
随堂检测
2. [2021·江苏盐城校级期中]函数y=2????的图像大致是( B )
?
A B C D
解析:∵y=????????,k=2>0, ∴该函数的图像分别位于第一、第三象限.故选B.
?
B
3.如图,反比例函数y=????????的图像可能是( D )
?
A B
C D
D
解析:A.∵反比例函数的图像分别位于第一、第三象限或第二、第四象限,∴此选项不符合题意.B.k=-2×6=-12,k=4×(-2)=-8.∵-12≠-8,∴此选项不符合题意.C.k=4×2=8,k=-2×(-2)=4.∵8≠4,∴此选项不符合题意.D.k=4×2=8,k=-2×(-4)=8.∵8=8,∴此选项符合题意.故选D.
4. 已知反比例函数 的图象过点(-2,-3),函
数图象上有两点 A( ,y1),B(5,y2),则 y1与y2
的大小关系为 ( )
A. y1 > y2
B. y1 = y2
C. y1 < y2
D. 无法确定
C
提示:由题可知反比例函数的解析式为 ,因为6>0,且 A,B 两点均在该函数图象的第一象限部分,根据 >5,可知y1,y2的大小关系.
5. 在同一直角坐标系中,函数 y = 2x 与 的图象大致是 ( )
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
B
6.(一题多解)[2022·天津中考]若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=8????的图像上,则x1,x2,x3的大小关系是( B )
?
A.x1<x2<x3
B.x2<x3<x1
C.x1<x3<x2
D.x2<x1<x3
解析:∵点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=????????的图像上,∴x1=????????=4,x2=?????????=-8,x3=????????=2.又∵-8<2<4,∴x2<x3<x1.故选B.
?
B
一题多解
(图像法)作出反比例函数y=8????的图像,将点A,B,C分别在该图像上标出,如答图.由图像可知,x2<x3<x1.故选B.
?
(第4题答图)
7. (易错题)[2022·河北石家庄三模]对于反比例函数y=6????,下列说法错误的是( C )
?
A.它的图像分别位于第一、第三象限
B.它的图像必经过点(2,3)
C.y随x的增大而减小
D.它的图像不可能与坐标轴相交
C
解析:根据反比例函数的性质对这四个选项逐一分析.A.∵反比例函数y=????????的比例系数6>0,∴此函数的图像分别位于第一、第三象限,此选项说法正确;B.∵当x=2时,y=3,∴反比例函数y=????????的图像必经过点(2,3),此选项说法正确;C.∵反比例函数y=????????的图像分别位于第一、第三象限,∴在每一个象限内,y随x的增大而减小,此选项说法错误;D.它的图像不可能与坐标轴相交,此选项说法正确.故选C.
?
8. 若ab<0,则正比例函数y=ax与反比例函数y=????????在同一平面直角坐标系中的大致图像是( B )
?
A B C D
B
解析:∵ab<0,∴分两种情况:(1)当a>0,b<0时,正比例函数y=ax的图像经过原点和第一、第三象限,反比例函数y=????????的图像位于第二、第四象限,无选项符合;(2)当a<0,b>0时,正比例函数y=ax的图像经过原点和第二、第四象限,反比例函数y=????????的图像位于第一、第三象限,选项B符合.故选B.
?
9.新趋势 跨学科实践 [2022·浙江丽水中考]已知电灯电路两端的电压U为220 V,通过灯泡的电流I(A)的最大限度不得超过0.11 A.设选用灯泡的电阻为R(Ω),下列说法正确的是( A )
A.R至少为2 000
B.R至多为2 000
C.R至少为24.2
D.R至多为24.2
解析:∵电压U(V)一定时,电流I(A)与灯泡的电阻R(Ω)成反比例,∴I=????????.∵已知电灯电路两端的电压U为220 V,∴I=????????????????.∵通过灯泡的电流I(A)的最大限度不得超过0.11 A,∴????????????????≤0.11,∴R≥2 000.故选A.
?
A
10.[2021·河南南阳校级一模]如图,△ABC的三个顶点的坐标分别为A(1,3),B(5,3),C(5,5).若反比例函数y=????????在第一象限内的图像与△ABC有交点,则k的取值范围是( C )
?
(第9题图)
A.1≤k≤15
B.3≤k≤15
C.3≤k≤25
D.15≤k≤25
C
解析:∵△ABC的三个顶点的坐标分别为A(1,3),B(5,3),C(5,5),∴△ABC是直角三角形.当反比例函数y=????????的图像经过点A时,k的值最小;经过点C时,k的值最大.∴k最小=1×3=3,k最大=5×5=25,∴3≤k≤25.故选C.
?
11. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
12. 在反比例函数 (k>0) 的图象上有两点 A (x1,y1),B (x2,y2), 且 x1>x2>0,则 y1-y2 0.
<
13. [2022·辽宁沈阳模拟]已知点P(m+3,2),Q3,????3都在反比例函数y=????????的图像上,则k的值为? -6 ?.?
?
解析:∵点P(m+3,2),Q????,????????都在反比例函数y=????????的图像上,∴k=2(m+3)=3×????????,∴m=-6,∴k=-6.
?
-6
14.[2022·上海浦东新区二模]已知反比例函数y=3?????????,如果在每一个象限内,y随自变量x的增大而增大,那么a的取值范围为? a>3 ?.?
?
解析:根据题意,得3-a<0,解得a>3.
a>3
15. [2021·广东广州中考]一元二次方程x2-4x+m=0有两个相等的实数根,A(x1,y1),B(x2,y2)是反比例函数y=????????图像上的两个点,若x1<x2<0,则y1? > ?y2(填“<”或“>”或“=”).?
?
解析:∵一元二次方程x2-4x+m=0有两个相等的实数根,∴Δ=16-4m=0,解得m=4.∵m>0,∴反比例函数y=????????的图像分别位于第一、第三象限,在每一个象限内,y随x的增大而减小.∵x1<x2<0,∴y1>y2.
?
>
方法总结:已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可.
16.已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.
17. [2021·河南南阳校级期中]已知反比例函数y=1?2????????(m为常数)的图像位于第一、第三象限.
?
(1)求m的取值范围.
解:(1)由题意,得1-2m>0,解得m<????????.
?
(第13题图)
(2)如图,若该反比例函数的图像经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0),求出该反比例函数的解析式.
解:(2)∵四边形ABOD为平行四边形,B(-2,0),∴AD∥OB,AD=OB=2.
又∵点A的坐标为(0,3),∴点D的坐标为(2,3),∴1-2m=2×3=6.
故该反比例函数的解析式为y=????????.
?
(3)若点E(x1,y1),F(x2,y2)都在该反比例函数的图像上,且x1>x2>0,则y1和y2有怎样的大小关系?
解:(3)∵x1>x2>0,∴E,F两点都在第一象限.
∵在第一象限内,y随x的增大而减小,∴y1<y2.
研究正比例函数图像
①图像所在的象限
②图像的增减性
反比例函数性质:
正比例函数
的性质
①当 k>0时,函数图象的两个
分支分别在 内,
当 k<0时,函数图象的两个
分支分别在 内,
②当自变量x逐渐 时,
y的值则随着逐渐 .
当自变量x逐渐 时,
y的值则随着逐渐 .
③图象的两个分支都无限接近于x轴和y轴,但不会与
x轴和y轴相交.
第一、三象限
第二、四象限
增大
减少
增大
增大
②在每个象限内,
当自变量x逐渐 时,
y的值则随着逐渐 .
减小
增大
在每个象限内,
当自变量x逐渐 时,
y的值则随着逐渐 .
增大
增大
对比
课堂小结
第18章 正比例函数与反比例函数
18.3反比例函数的图像和性质(第2课时)
1.经历画反比例函数的图象、归纳得到反比例函数的图象特征和性质的过程 (重点、难点)
2.会画反比例函数图象,了解和掌握反比例函数的图象和性质.(重点)
学习目标
2、其定义域是什么?
复习引入
1、什么是反比例函数?
形如_____________________是反比例函数.
不等于零的一切实数
今天学习反比例函数的图像与性质
(即 )
操作1:画反比例函数 的图像
画反比例函数的图像
画函数图象有哪些步骤?
列表、描点、连线
自变量x的取值范围是什么?
通常在0的附近,正数和负数至少各取5个数
自变量x取哪些数比较容易计算出y的值呢?
操作1:画反比例函数 的图像
把各点用光滑的曲线连接,再向两方伸展
第一象限和第三象限各有一支曲线
探索
两支曲线,分别在第一、三象限.
反比例函数 的图像与正比例函数有何区别?
图像不会与坐标轴相交,
即图像向两方无限延伸.
图像是否会与坐标轴相交?为什么?
探索
在第一象限内,当自变量x的取值不断增大,y的值不断减小!
当自变量x的取值不断减小,y的值不断增大!
函数图像越来越接近x轴,但不与x轴相交!
函数图象越来越接近y轴,但不与y轴相交!
为什么每支曲线都无限接近于坐标轴?
操作2:画反比例函数 的图像
同样是两支曲线!
两支曲线在第二、四象限!
函数图像不会与坐标轴相交,即图像向两方无限延伸.
反比例函数 图像和 有何相同和区别?
图像是否会与坐标轴相交?
反比例函数 的图像叫做双曲线.
小结
双曲线有何特点呢?
双曲线有两支,每支都向两方伸展,无限接近坐标轴,但与坐标轴不相交.
操作3:(1)画反比例函数 和 的图像
探索规律
观察以上反比例函数的图像并思考问题:
(1)函数图像分别位于哪几个象限?
(2)在每一个象限内,y随x的变化有怎样的变化?
(3)函数图像会与坐标轴相交吗?为什么?
一般地,反比例函数 y= ( k为常数, k≠0 )的图像是双曲线,它具有以下性质:
反比例函数的性质
(1)当k>0时,函数图像的两支分别在第一、三象限,在每一
个象限内,当自变量x的值逐渐增大时,y的值随着逐渐减小。
(2)当k<0时,函数图像的两支分别在第二、四象限,在每一
个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大。
(3)图像的两支都无限接近于x轴和y轴,但不会与x轴和y轴相交。
2010年世博会在上海召开,设计专家计划在园区内一块休息区域种植8km2 的植被,如果按长方形种植,它们的长与宽分别如下图:这些长方形的长与宽有什么关系?
8
1
2
1
2
8
单位:km
4
4
x
y
o
1
8
2
4
4
2
8
1
A1
A2
A3
A4
讨论1:请你说出A1、A2、A3、A4四个点的
纵坐标y和横坐标x满足怎样的函数关系?
(1,8)
(2,4)
(4,2)
(8,1)
设点P(m,n)是该函数图象上任意一点,过P分别作x轴y轴的垂线段,垂足为A、B,构成的长方形面积是多少?
P(m,n)
A
B
1.画反比例函数 和 的图像
课本练习
在其图像所在的每个象限内,y的值随x的值的增大而
减小的函数是________________.
其中,图像位于第二、四象限的函数是
_________________________________;
3、已知下列反比例函数:
4.如果反比例函数 ( 是常数,
),的图像在第二、四象限,那么正
比例函数 ( 是常数, )的
图像经过哪几个象限?
1. 反比例函数 的图象大致是 ( )
C
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
随堂检测
2. [2021·江苏盐城校级期中]函数y=2????的图像大致是( B )
?
A B C D
解析:∵y=????????,k=2>0, ∴该函数的图像分别位于第一、第三象限.故选B.
?
B
3.如图,反比例函数y=????????的图像可能是( D )
?
A B
C D
D
解析:A.∵反比例函数的图像分别位于第一、第三象限或第二、第四象限,∴此选项不符合题意.B.k=-2×6=-12,k=4×(-2)=-8.∵-12≠-8,∴此选项不符合题意.C.k=4×2=8,k=-2×(-2)=4.∵8≠4,∴此选项不符合题意.D.k=4×2=8,k=-2×(-4)=8.∵8=8,∴此选项符合题意.故选D.
4. 已知反比例函数 的图象过点(-2,-3),函
数图象上有两点 A( ,y1),B(5,y2),则 y1与y2
的大小关系为 ( )
A. y1 > y2
B. y1 = y2
C. y1 < y2
D. 无法确定
C
提示:由题可知反比例函数的解析式为 ,因为6>0,且 A,B 两点均在该函数图象的第一象限部分,根据 >5,可知y1,y2的大小关系.
5. 在同一直角坐标系中,函数 y = 2x 与 的图象大致是 ( )
O
x
y
O
x
y
O
x
y
O
x
y
A.
B.
C.
D.
B
6.(一题多解)[2022·天津中考]若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=8????的图像上,则x1,x2,x3的大小关系是( B )
?
A.x1<x2<x3
B.x2<x3<x1
C.x1<x3<x2
D.x2<x1<x3
解析:∵点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=????????的图像上,∴x1=????????=4,x2=?????????=-8,x3=????????=2.又∵-8<2<4,∴x2<x3<x1.故选B.
?
B
一题多解
(图像法)作出反比例函数y=8????的图像,将点A,B,C分别在该图像上标出,如答图.由图像可知,x2<x3<x1.故选B.
?
(第4题答图)
7. (易错题)[2022·河北石家庄三模]对于反比例函数y=6????,下列说法错误的是( C )
?
A.它的图像分别位于第一、第三象限
B.它的图像必经过点(2,3)
C.y随x的增大而减小
D.它的图像不可能与坐标轴相交
C
解析:根据反比例函数的性质对这四个选项逐一分析.A.∵反比例函数y=????????的比例系数6>0,∴此函数的图像分别位于第一、第三象限,此选项说法正确;B.∵当x=2时,y=3,∴反比例函数y=????????的图像必经过点(2,3),此选项说法正确;C.∵反比例函数y=????????的图像分别位于第一、第三象限,∴在每一个象限内,y随x的增大而减小,此选项说法错误;D.它的图像不可能与坐标轴相交,此选项说法正确.故选C.
?
8. 若ab<0,则正比例函数y=ax与反比例函数y=????????在同一平面直角坐标系中的大致图像是( B )
?
A B C D
B
解析:∵ab<0,∴分两种情况:(1)当a>0,b<0时,正比例函数y=ax的图像经过原点和第一、第三象限,反比例函数y=????????的图像位于第二、第四象限,无选项符合;(2)当a<0,b>0时,正比例函数y=ax的图像经过原点和第二、第四象限,反比例函数y=????????的图像位于第一、第三象限,选项B符合.故选B.
?
9.新趋势 跨学科实践 [2022·浙江丽水中考]已知电灯电路两端的电压U为220 V,通过灯泡的电流I(A)的最大限度不得超过0.11 A.设选用灯泡的电阻为R(Ω),下列说法正确的是( A )
A.R至少为2 000
B.R至多为2 000
C.R至少为24.2
D.R至多为24.2
解析:∵电压U(V)一定时,电流I(A)与灯泡的电阻R(Ω)成反比例,∴I=????????.∵已知电灯电路两端的电压U为220 V,∴I=????????????????.∵通过灯泡的电流I(A)的最大限度不得超过0.11 A,∴????????????????≤0.11,∴R≥2 000.故选A.
?
A
10.[2021·河南南阳校级一模]如图,△ABC的三个顶点的坐标分别为A(1,3),B(5,3),C(5,5).若反比例函数y=????????在第一象限内的图像与△ABC有交点,则k的取值范围是( C )
?
(第9题图)
A.1≤k≤15
B.3≤k≤15
C.3≤k≤25
D.15≤k≤25
C
解析:∵△ABC的三个顶点的坐标分别为A(1,3),B(5,3),C(5,5),∴△ABC是直角三角形.当反比例函数y=????????的图像经过点A时,k的值最小;经过点C时,k的值最大.∴k最小=1×3=3,k最大=5×5=25,∴3≤k≤25.故选C.
?
11. 下列关于反比例函数 的图象的三个结论:
(1) 经过点 (-1,12) 和点 (10,-1.2);
(2) 在每一个象限内,y 随 x 的增大而减小;
(3) 双曲线位于二、四象限.
其中正确的是 (填序号).
(1)(3)
12. 在反比例函数 (k>0) 的图象上有两点 A (x1,y1),B (x2,y2), 且 x1>x2>0,则 y1-y2 0.
<
13. [2022·辽宁沈阳模拟]已知点P(m+3,2),Q3,????3都在反比例函数y=????????的图像上,则k的值为? -6 ?.?
?
解析:∵点P(m+3,2),Q????,????????都在反比例函数y=????????的图像上,∴k=2(m+3)=3×????????,∴m=-6,∴k=-6.
?
-6
14.[2022·上海浦东新区二模]已知反比例函数y=3?????????,如果在每一个象限内,y随自变量x的增大而增大,那么a的取值范围为? a>3 ?.?
?
解析:根据题意,得3-a<0,解得a>3.
a>3
15. [2021·广东广州中考]一元二次方程x2-4x+m=0有两个相等的实数根,A(x1,y1),B(x2,y2)是反比例函数y=????????图像上的两个点,若x1<x2<0,则y1? > ?y2(填“<”或“>”或“=”).?
?
解析:∵一元二次方程x2-4x+m=0有两个相等的实数根,∴Δ=16-4m=0,解得m=4.∵m>0,∴反比例函数y=????????的图像分别位于第一、第三象限,在每一个象限内,y随x的增大而减小.∵x1<x2<0,∴y1>y2.
?
>
方法总结:已知某个函数为反比例函数,只需要根据反比例函数的定义列出方程(组)求解即可.
16.已知反比例函数 ,y 随 x 的增大而增大,求a的值.
解:由题意得a2+a-7=-1,且a-1<0.
解得 a=-3.
17. [2021·河南南阳校级期中]已知反比例函数y=1?2????????(m为常数)的图像位于第一、第三象限.
?
(1)求m的取值范围.
解:(1)由题意,得1-2m>0,解得m<????????.
?
(第13题图)
(2)如图,若该反比例函数的图像经过?ABOD的顶点D,点A,B的坐标分别为(0,3),(-2,0),求出该反比例函数的解析式.
解:(2)∵四边形ABOD为平行四边形,B(-2,0),∴AD∥OB,AD=OB=2.
又∵点A的坐标为(0,3),∴点D的坐标为(2,3),∴1-2m=2×3=6.
故该反比例函数的解析式为y=????????.
?
(3)若点E(x1,y1),F(x2,y2)都在该反比例函数的图像上,且x1>x2>0,则y1和y2有怎样的大小关系?
解:(3)∵x1>x2>0,∴E,F两点都在第一象限.
∵在第一象限内,y随x的增大而减小,∴y1<y2.
研究正比例函数图像
①图像所在的象限
②图像的增减性
反比例函数性质:
正比例函数
的性质
①当 k>0时,函数图象的两个
分支分别在 内,
当 k<0时,函数图象的两个
分支分别在 内,
②当自变量x逐渐 时,
y的值则随着逐渐 .
当自变量x逐渐 时,
y的值则随着逐渐 .
③图象的两个分支都无限接近于x轴和y轴,但不会与
x轴和y轴相交.
第一、三象限
第二、四象限
增大
减少
增大
增大
②在每个象限内,
当自变量x逐渐 时,
y的值则随着逐渐 .
减小
增大
在每个象限内,
当自变量x逐渐 时,
y的值则随着逐渐 .
增大
增大
对比
课堂小结
