人教新版六年级上册《确定起跑线》2023年同步练习卷(含解析)
文档属性
| 名称 | 人教新版六年级上册《确定起跑线》2023年同步练习卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 169.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 09:15:34 | ||
图片预览


文档简介
人教新版六年级上册《确定起跑线》2023年同步练习卷
一、填空题
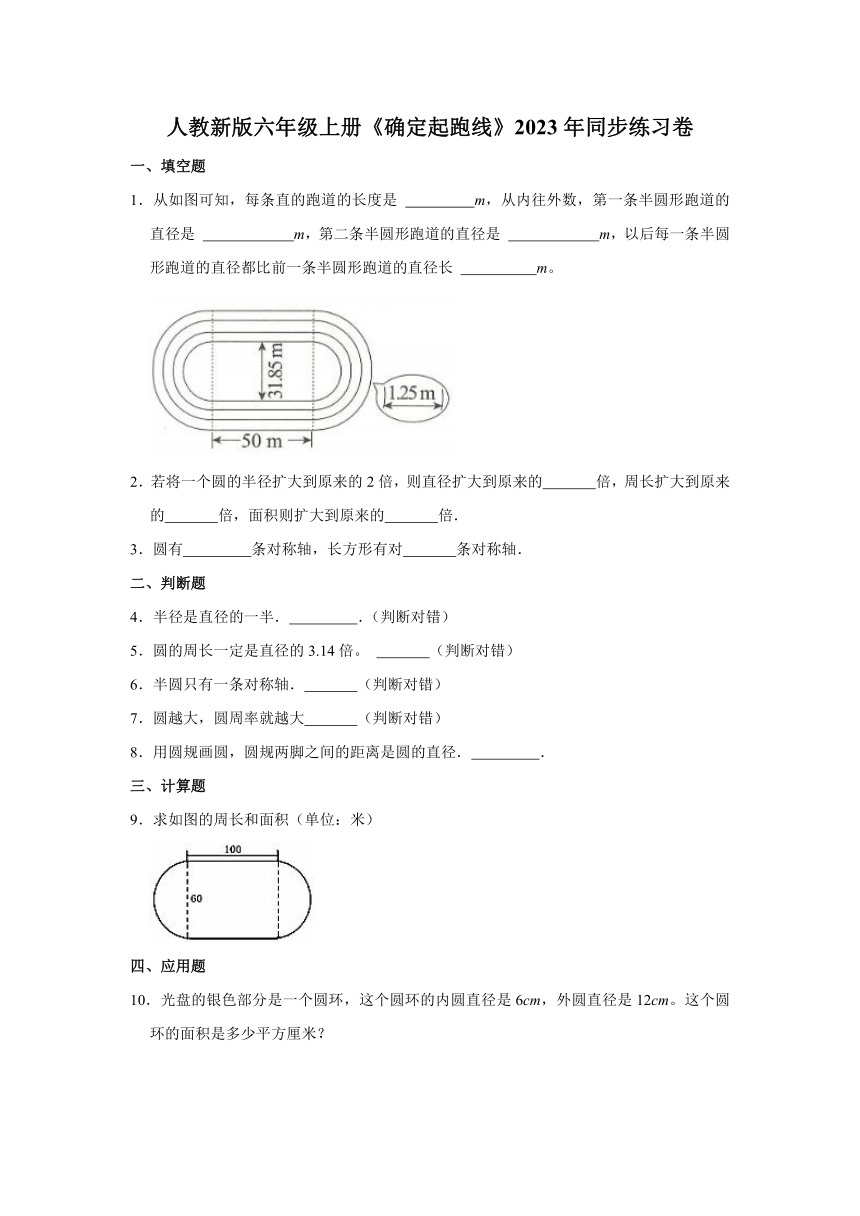
1.从如图可知,每条直的跑道的长度是 m,从内往外数,第一条半圆形跑道的直径是 m,第二条半圆形跑道的直径是 m,以后每一条半圆形跑道的直径都比前一条半圆形跑道的直径长 m。
2.若将一个圆的半径扩大到原来的2倍,则直径扩大到原来的 倍,周长扩大到原来的 倍,面积则扩大到原来的 倍.
3.圆有 条对称轴,长方形有对 条对称轴.
二、判断题
4.半径是直径的一半. .(判断对错)
5.圆的周长一定是直径的3.14倍。 (判断对错)
6.半圆只有一条对称轴. (判断对错)
7.圆越大,圆周率就越大 (判断对错)
8.用圆规画圆,圆规两脚之间的距离是圆的直径. .
三、计算题
9.求如图的周长和面积(单位:米)
四、应用题
10.光盘的银色部分是一个圆环,这个圆环的内圆直径是6cm,外圆直径是12cm。这个圆环的面积是多少平方厘米?
11.一个挂钟分针长8cm,从中午12时整到下午2时整,分针针尖走过的路程是多少厘米?
五、解答题
12.在最内侧跑道长度为200m的田径场进行200m赛跑时,相邻两条跑道的起跑线应该相差多少米?(π取3.14,结果保留两位小数)
(1)方法一:求出各条跑道的长,再求长度差。
第一条跑道全长:50×2+3.14×31.85≈200.01(m)
第二条跑道全长:
第三条跑道全长:
第四条跑道全长:
第二条跑道与第一条跑道长度差:
第三条跑道与第二条跑道长度差:
第四条跑道与第三条跑道长度差:
答:相邻两条跑道的起跑线应该相差 m。
(2)方法二:因为直道的长度都相等,所以只要求出相邻两条弯道的长度差就求出了相邻两条跑道的长度差。第一条跑道弯道的长:3.14×31.85≈100.01(m)
第二条跑道弯道的长:
第三条跑道弯道的长:
第四条跑道弯道的长:
第二条跑道与第一条跑道长度差:
第三条跑道与第二条跑道长度差:
第四条跑道与第三条跑道长度差:
答:相邻两条跑道的起跑线应该相差 m。
(3)方法三:求出相邻两条跑道的直径差,就可以求出相邻两条弯道的长度差,也就是相邻两条跑道的长度差。
算式:
答:相邻两条跑道的起跑线应该相差 m。
人教新版六年级上册《确定起跑线》2023年同步练习卷
参考答案与试题解析
一、填空题
1.【解答】解:31.85+1.25×2=34.35(米)
1.25×2=2.5(米)
答:每条直的跑道的长度是50m,从内往外数,第一条半圆形跑道的直径是31.85m,第二条半圆形跑道的直径是34.35米,以后每一条半圆形跑道的直径都比前一条半圆形跑道的直径长2.5米。
故答案为:50;31.85;34.35;2.5。
2.【解答】解:设原来圆的半径为r,则直径为2r,
圆的周长为:2πr,
圆的面积为:πr2,
半径扩大2倍后,圆的半径为2r,圆的直径为4r,
圆的周长为:4πr,
圆的面积为:(2r)2π=4πr2,
则直径扩大到原来的:4r÷2r=2,
周长扩大到原来的:4πr÷2πr=2,
面积扩大到原来的:4πr2÷πr2=4;
答:直径扩大到原来的2倍,周长扩大到原来的2倍,面积则扩大到原来的4倍.
故答案为:2,2,4.
3.【解答】解:圆的对称轴有无数条,分别是经过圆心的每条直线;
长方形的对称轴有2条,分别是对边中点所在的直线;
故答案为:无数;2.
二、判断题
4.【解答】解:由分析知:半径是直径的一半,说法错误;
故答案为:×.
5.【解答】解:由圆周率的含义可知:
圆的周长一定是它直径的π倍,而不是3.14倍,因为3.14只是圆周率的近似值。
故答案为:×。
6.【解答】解:如图所示,半圆有1条对称轴:
故答案为:√.
7.【解答】解:因为圆周率是圆的周长和它直径的比值,是一个定值,不随圆的大小而改变.
故答案为:×.
8.【解答】解:由分析知:用圆规画圆,圆规两脚之间的距离是圆的直径,说法错误;
故答案为:×.
三、计算题
9.【解答】解:3.14×60+100×2
=188.4+200
=388.4(米)
3.14×(60÷2) +60×100
=3.14×900+6000
=2826+6000
=8826(平方米)
答:这个图形的周长是388.4米,面积是8826平方米。
四、应用题
10.【解答】解:3.14×[(12÷2)2﹣(6÷2)2]
=3.14×(36﹣9)
=3.14×25
=78.5(平方厘米)
答:圆环面积是78.5平方厘米。
11.【解答】解:2×3.14×8×2
=6.28×16
=100.48(厘米)
答:分针针尖走过的路程是100.84厘米。
五、解答题
12.【解答】解:方法一:求出各条跑道的长,再求长度差.算式如下:
第一条跑道全长:50×2+3.14×31.85≈200.01(m)。
第二条跑道全长:
50×2+3.14×(31.85+2×1.25)
=100+3.14×34.35
100+107.859
≈207.86(m)
第三条跑道全长:
50×2+3.14×(31.85+2×1.25+2×1.25)
=100+3.14×36.85
=100+115.709
≈215.71(m)
第四条跑道全长:
50×2+3.14×(31.85+2×1.25+2×1.25+2×1.25)
=100+3.14×39.35
=100+123.559
≈223.56(m)
第二条跑道和第一条跑道长度差:207.86﹣200.01=7.85(m)
第三条跑道和第二条跑道长度差:215.71﹣207.86=7.85(m)
第四条跑道和第三条跑道长度差:223.56﹣215.71=7.85(m)
答:各跑道的长相差约 7.85m。
方法二:閃为直道的长度都相等,所以求相邻跑道长度之间的差就是求其弯道长度之间的
差.算式如下:第一条跑道弯道的长:3.14×31.85≈100.01(m)
第二条跑道弯道的长:
3.14×(31.85+1.25×2)
=3.14×34.35
≈107.86(m)
第三条跑道弯道的长:
3.14×(31.85+1.25×2+1.25×2)
=3.14×36.85
≈115.71(m)
第四条跑道弯道的长:
3.14×(31.85+1.25×2+1.25×2+1.25×2)
=3.14×39.35
≈123.56(m)
第二条跑道和第一条跑道长度差:107.86﹣100.01=7.85(m)
第三条跑道和第二条跑道长度差:115.71﹣107.86=7.85(m)
第四条跑道和第三条跑道长度差:123.56﹣115.71=7.85(m)
答:各跑道的长相差约 7.85m。
方法三:先求出相邻跑道的直径差,再求出相邻两条弯道的长度差,也就是相邻两条跑道的长度差。
算式:3.14×(1.25×2)
=3.14×2.5
=7.85(m)
答:各跑道的长相差约7.85。
故答案为:50×2+3.14×(31.85+2×1.25)≈207.86(m),50×2+3.14×(31.85+2×1.25+2×1.25)≈215.71(m),50×2+3.14×(31.85+2×1.25+2×1.25+2×1.25)≈223.56(m),207.86﹣200.01=7.85(m),215.71﹣207.86=7.85(m),223.56﹣215.71=7.85(m),7.85m;3.14×(31.85+1.25×2)≈107.86(m),3.14×(31.85+1.25×2+1.25×2)≈115.71(m),3.14×(31.85+1.25×2+1.25×2+1.25×2)≈123.56(m),107.86﹣100.01=7.85(m),115.71﹣107.86=7.85(m),123.56﹣115.71=7.85(m),7.85m;3.14×(1.25×2)=7.85(m),7.85m。
一、填空题
1.从如图可知,每条直的跑道的长度是 m,从内往外数,第一条半圆形跑道的直径是 m,第二条半圆形跑道的直径是 m,以后每一条半圆形跑道的直径都比前一条半圆形跑道的直径长 m。
2.若将一个圆的半径扩大到原来的2倍,则直径扩大到原来的 倍,周长扩大到原来的 倍,面积则扩大到原来的 倍.
3.圆有 条对称轴,长方形有对 条对称轴.
二、判断题
4.半径是直径的一半. .(判断对错)
5.圆的周长一定是直径的3.14倍。 (判断对错)
6.半圆只有一条对称轴. (判断对错)
7.圆越大,圆周率就越大 (判断对错)
8.用圆规画圆,圆规两脚之间的距离是圆的直径. .
三、计算题
9.求如图的周长和面积(单位:米)
四、应用题
10.光盘的银色部分是一个圆环,这个圆环的内圆直径是6cm,外圆直径是12cm。这个圆环的面积是多少平方厘米?
11.一个挂钟分针长8cm,从中午12时整到下午2时整,分针针尖走过的路程是多少厘米?
五、解答题
12.在最内侧跑道长度为200m的田径场进行200m赛跑时,相邻两条跑道的起跑线应该相差多少米?(π取3.14,结果保留两位小数)
(1)方法一:求出各条跑道的长,再求长度差。
第一条跑道全长:50×2+3.14×31.85≈200.01(m)
第二条跑道全长:
第三条跑道全长:
第四条跑道全长:
第二条跑道与第一条跑道长度差:
第三条跑道与第二条跑道长度差:
第四条跑道与第三条跑道长度差:
答:相邻两条跑道的起跑线应该相差 m。
(2)方法二:因为直道的长度都相等,所以只要求出相邻两条弯道的长度差就求出了相邻两条跑道的长度差。第一条跑道弯道的长:3.14×31.85≈100.01(m)
第二条跑道弯道的长:
第三条跑道弯道的长:
第四条跑道弯道的长:
第二条跑道与第一条跑道长度差:
第三条跑道与第二条跑道长度差:
第四条跑道与第三条跑道长度差:
答:相邻两条跑道的起跑线应该相差 m。
(3)方法三:求出相邻两条跑道的直径差,就可以求出相邻两条弯道的长度差,也就是相邻两条跑道的长度差。
算式:
答:相邻两条跑道的起跑线应该相差 m。
人教新版六年级上册《确定起跑线》2023年同步练习卷
参考答案与试题解析
一、填空题
1.【解答】解:31.85+1.25×2=34.35(米)
1.25×2=2.5(米)
答:每条直的跑道的长度是50m,从内往外数,第一条半圆形跑道的直径是31.85m,第二条半圆形跑道的直径是34.35米,以后每一条半圆形跑道的直径都比前一条半圆形跑道的直径长2.5米。
故答案为:50;31.85;34.35;2.5。
2.【解答】解:设原来圆的半径为r,则直径为2r,
圆的周长为:2πr,
圆的面积为:πr2,
半径扩大2倍后,圆的半径为2r,圆的直径为4r,
圆的周长为:4πr,
圆的面积为:(2r)2π=4πr2,
则直径扩大到原来的:4r÷2r=2,
周长扩大到原来的:4πr÷2πr=2,
面积扩大到原来的:4πr2÷πr2=4;
答:直径扩大到原来的2倍,周长扩大到原来的2倍,面积则扩大到原来的4倍.
故答案为:2,2,4.
3.【解答】解:圆的对称轴有无数条,分别是经过圆心的每条直线;
长方形的对称轴有2条,分别是对边中点所在的直线;
故答案为:无数;2.
二、判断题
4.【解答】解:由分析知:半径是直径的一半,说法错误;
故答案为:×.
5.【解答】解:由圆周率的含义可知:
圆的周长一定是它直径的π倍,而不是3.14倍,因为3.14只是圆周率的近似值。
故答案为:×。
6.【解答】解:如图所示,半圆有1条对称轴:
故答案为:√.
7.【解答】解:因为圆周率是圆的周长和它直径的比值,是一个定值,不随圆的大小而改变.
故答案为:×.
8.【解答】解:由分析知:用圆规画圆,圆规两脚之间的距离是圆的直径,说法错误;
故答案为:×.
三、计算题
9.【解答】解:3.14×60+100×2
=188.4+200
=388.4(米)
3.14×(60÷2) +60×100
=3.14×900+6000
=2826+6000
=8826(平方米)
答:这个图形的周长是388.4米,面积是8826平方米。
四、应用题
10.【解答】解:3.14×[(12÷2)2﹣(6÷2)2]
=3.14×(36﹣9)
=3.14×25
=78.5(平方厘米)
答:圆环面积是78.5平方厘米。
11.【解答】解:2×3.14×8×2
=6.28×16
=100.48(厘米)
答:分针针尖走过的路程是100.84厘米。
五、解答题
12.【解答】解:方法一:求出各条跑道的长,再求长度差.算式如下:
第一条跑道全长:50×2+3.14×31.85≈200.01(m)。
第二条跑道全长:
50×2+3.14×(31.85+2×1.25)
=100+3.14×34.35
100+107.859
≈207.86(m)
第三条跑道全长:
50×2+3.14×(31.85+2×1.25+2×1.25)
=100+3.14×36.85
=100+115.709
≈215.71(m)
第四条跑道全长:
50×2+3.14×(31.85+2×1.25+2×1.25+2×1.25)
=100+3.14×39.35
=100+123.559
≈223.56(m)
第二条跑道和第一条跑道长度差:207.86﹣200.01=7.85(m)
第三条跑道和第二条跑道长度差:215.71﹣207.86=7.85(m)
第四条跑道和第三条跑道长度差:223.56﹣215.71=7.85(m)
答:各跑道的长相差约 7.85m。
方法二:閃为直道的长度都相等,所以求相邻跑道长度之间的差就是求其弯道长度之间的
差.算式如下:第一条跑道弯道的长:3.14×31.85≈100.01(m)
第二条跑道弯道的长:
3.14×(31.85+1.25×2)
=3.14×34.35
≈107.86(m)
第三条跑道弯道的长:
3.14×(31.85+1.25×2+1.25×2)
=3.14×36.85
≈115.71(m)
第四条跑道弯道的长:
3.14×(31.85+1.25×2+1.25×2+1.25×2)
=3.14×39.35
≈123.56(m)
第二条跑道和第一条跑道长度差:107.86﹣100.01=7.85(m)
第三条跑道和第二条跑道长度差:115.71﹣107.86=7.85(m)
第四条跑道和第三条跑道长度差:123.56﹣115.71=7.85(m)
答:各跑道的长相差约 7.85m。
方法三:先求出相邻跑道的直径差,再求出相邻两条弯道的长度差,也就是相邻两条跑道的长度差。
算式:3.14×(1.25×2)
=3.14×2.5
=7.85(m)
答:各跑道的长相差约7.85。
故答案为:50×2+3.14×(31.85+2×1.25)≈207.86(m),50×2+3.14×(31.85+2×1.25+2×1.25)≈215.71(m),50×2+3.14×(31.85+2×1.25+2×1.25+2×1.25)≈223.56(m),207.86﹣200.01=7.85(m),215.71﹣207.86=7.85(m),223.56﹣215.71=7.85(m),7.85m;3.14×(31.85+1.25×2)≈107.86(m),3.14×(31.85+1.25×2+1.25×2)≈115.71(m),3.14×(31.85+1.25×2+1.25×2+1.25×2)≈123.56(m),107.86﹣100.01=7.85(m),115.71﹣107.86=7.85(m),123.56﹣115.71=7.85(m),7.85m;3.14×(1.25×2)=7.85(m),7.85m。
