苏科版八年级数学上册试题 第三章《勾股定理》单元检测卷(文字版,有答案)
文档属性
| 名称 | 苏科版八年级数学上册试题 第三章《勾股定理》单元检测卷(文字版,有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 21:03:45 | ||
图片预览




文档简介
第三章《勾股定理》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
2.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,AC=3,则BD的长是( )
A.2 B.3.5 C.3 D.2.5
3.如图,在△ABC中,∠B=90°,AB=2,BC=4.四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.12 C.18 D.20
4.如图,快艇从A地出发,要到距离A地10海里的C地去,先沿北偏东70°方向走了8海里,到达B地,然后再从B地走了6海里到达C地,此时快艇位于B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
5.如图所示是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案,现在有五种正方形纸片,面积分别是2,3,4,5,6,选取其中三块(可重复选取),按如图所示方式组成图案,使所围成的三角形是直角三角形,则选取的三块纸片的面积不可以是( )
A.3,4,5 B.2,2,4 C.3,3,6 D.2,4,6
6.如图,在4×4的正方形网格中,每一格长度为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以AB,CD,EF为边能构成一个直角三角形,则点F的位置有( )
A.1处 B.2处 C.3处 D.4处
7.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
8.如图,有一个圆柱,底面圆的直径ABcm,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为( )
A.9cm B.10cm C.11cm D.12cm
9.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”根据题意,可得秋千的绳索长为( )
A.10尺 B.14.5尺 C.13尺 D.17尺
10.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12 B.15 C.20 D.25
二.填空题(共6小题,满分18分,每小题3分)
11.如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),则xy= .
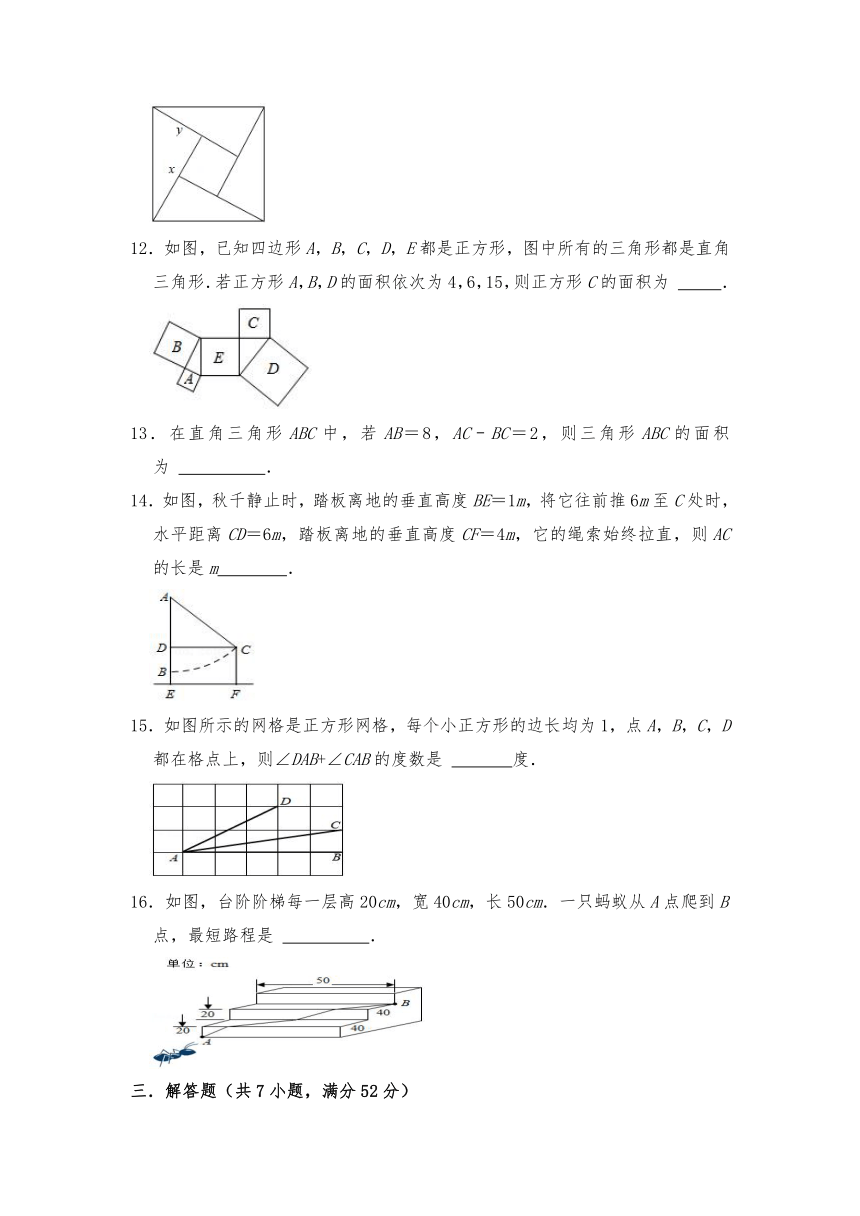
12.如图,已知四边形A,B,C,D,E都是正方形,图中所有的三角形都是直角三角形.若正方形A,B,D的面积依次为4,6,15,则正方形C的面积为 .
13.在直角三角形ABC中,若AB=8,AC﹣BC=2,则三角形ABC的面积为 .
14.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m .
15.如图所示的网格是正方形网格,每个小正方形的边长均为1,点A,B,C,D都在格点上,则∠DAB+∠CAB的度数是 度.
16.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是 .
三.解答题(共7小题,满分52分)
17.(6分)如图,已知△ABC中,AB=AC,BC=5,D为AB上一点,CD=4,BD=3.
(1)求证:∠BDC=90°;
(2)求AC的长.
18.(6分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的俯视示意图),今推开双门,门框上点C和点D到门槛AB的距离DE为1尺(1尺=10寸),双门间的缝隙CD为2寸,求门宽AB的长是多少寸?
19.(8分)已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
20.(8分)在△ABC中,
(1)如图1,AC=15,AD=9,CD=12,BC=20,求△ABC的面积;
(2)如图2,AC=13,BC=20,AB=11,求△ABC的面积.
21.(8分)如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
22.(8分)勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23.(8分)如图是5×6的网格.
(1)如图(1),A,B,C是网格中的三个格点(即小正方形的顶点),判断AC与BC的数量和位置关系,直接写出结论,不需要说明理由;
(2)如图(2),求∠1+∠2的度数(要求:画出示意图并给出推导过程).
答案
一.选择题
A.D.D.B.A.D.B.B.B.B.
二.填空题
11.22.5.
12.5.
13.15或60.
14.7.5.
15.45.
16.130cm.
三.解答题
17.(1)证明:∵BC=5,CD=4,BD=3,
∴42+32=52,
∴∠BDC=90°;
(2)解:在Rt△ADC中,∠ADC=180°﹣90°=90°,
依题意有AC2=(AB﹣3)2+CD2,即AC2=(AC﹣3)2+42,
解得AC.
故AC的长为.
18.解:取AB的中点O,过D作DE⊥AB于E,
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r(寸),DE=10寸,OECD=1寸,
∴AE=(r﹣1)寸,
在Rt△ADE中,
AE2+DE2=AD2,即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
答:门宽AB的长是101寸.
19.解:(1)在Rt△ABC中,由勾股定理得:BC4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
20.解:(1)∵CD2+AD2=144+81=225,AC2=225,
∴CD2+AD2=CA2,
∴△△ADC是直角三角形,
∴∠ADC=90°,
∴CD⊥AB,
∴∠ADC=90°,
∴BD16,
∴AB=AD+DB=16+9=25,
∴△ABC的面积25×12=150;
(2)过C作CD⊥BA的延长线于点D,
∵CD⊥AB,
∴∠CDB=90°,
设AD为x,DB=(x+11),由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣DB2,
即AC2﹣AD2=BC2﹣DB2,
则132﹣x2=202﹣(x+11)2,
解得:x=5,
∴CD12,
∴△ABC的面积 AB CD11×12=66.
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACDAB×ACAD×CD8×1512×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABCBC×AEAB AC,
∴17×AE=8×15,
解得:AE(m),
即小路AE的长为m.
22.解:(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.
23.解:(1)AC=BC且AC⊥BC.理由:
如图(1),∵CD=BE,∠ADC=∠CEB=90°,AD=CE,
∴△ACD≌△CBE(SAS),
∴AC=CB,∠ACD=∠CBE,
又∵∠CBE+∠BCE=90°,
∴∠ACD+∠BCE=90°,
∴∠ACB=180°﹣90°=90°,
∴AC⊥BC;
(2)如图(2),作△ABC,△DEF,
∵BC=FE,∠ABC=∠DFE,AB=DF,
∴△ABC △DFE(SAS),
∴∠ACB=∠DEF=∠2.
由图,结合勾股定理,得
,,AD=5,
∴AC2+DC2=5+20=25=AD2,
∴△ACD是直角三角形,且∠ACD=90°.
∵∠2+∠ACD+∠1=180°,
∴∠1+∠2=180°﹣∠ACD=180°﹣90°=90°.
一.选择题(共10小题,满分30分,每小题3分)
1.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
2.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,AC=3,则BD的长是( )
A.2 B.3.5 C.3 D.2.5
3.如图,在△ABC中,∠B=90°,AB=2,BC=4.四边形ADEC是正方形,则正方形ADEC的面积是( )
A.8 B.12 C.18 D.20
4.如图,快艇从A地出发,要到距离A地10海里的C地去,先沿北偏东70°方向走了8海里,到达B地,然后再从B地走了6海里到达C地,此时快艇位于B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
5.如图所示是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案,现在有五种正方形纸片,面积分别是2,3,4,5,6,选取其中三块(可重复选取),按如图所示方式组成图案,使所围成的三角形是直角三角形,则选取的三块纸片的面积不可以是( )
A.3,4,5 B.2,2,4 C.3,3,6 D.2,4,6
6.如图,在4×4的正方形网格中,每一格长度为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以AB,CD,EF为边能构成一个直角三角形,则点F的位置有( )
A.1处 B.2处 C.3处 D.4处
7.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
8.如图,有一个圆柱,底面圆的直径ABcm,高BC=12cm,P为BC的中点,一只蚂蚁从A点出发沿着圆柱的表面爬到P点的最短距离为( )
A.9cm B.10cm C.11cm D.12cm
9.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”根据题意,可得秋千的绳索长为( )
A.10尺 B.14.5尺 C.13尺 D.17尺
10.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12 B.15 C.20 D.25
二.填空题(共6小题,满分18分,每小题3分)
11.如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),则xy= .
12.如图,已知四边形A,B,C,D,E都是正方形,图中所有的三角形都是直角三角形.若正方形A,B,D的面积依次为4,6,15,则正方形C的面积为 .
13.在直角三角形ABC中,若AB=8,AC﹣BC=2,则三角形ABC的面积为 .
14.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m .
15.如图所示的网格是正方形网格,每个小正方形的边长均为1,点A,B,C,D都在格点上,则∠DAB+∠CAB的度数是 度.
16.如图,台阶阶梯每一层高20cm,宽40cm,长50cm.一只蚂蚁从A点爬到B点,最短路程是 .
三.解答题(共7小题,满分52分)
17.(6分)如图,已知△ABC中,AB=AC,BC=5,D为AB上一点,CD=4,BD=3.
(1)求证:∠BDC=90°;
(2)求AC的长.
18.(6分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的俯视示意图),今推开双门,门框上点C和点D到门槛AB的距离DE为1尺(1尺=10寸),双门间的缝隙CD为2寸,求门宽AB的长是多少寸?
19.(8分)已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
20.(8分)在△ABC中,
(1)如图1,AC=15,AD=9,CD=12,BC=20,求△ABC的面积;
(2)如图2,AC=13,BC=20,AB=11,求△ABC的面积.
21.(8分)如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
22.(8分)勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23.(8分)如图是5×6的网格.
(1)如图(1),A,B,C是网格中的三个格点(即小正方形的顶点),判断AC与BC的数量和位置关系,直接写出结论,不需要说明理由;
(2)如图(2),求∠1+∠2的度数(要求:画出示意图并给出推导过程).
答案
一.选择题
A.D.D.B.A.D.B.B.B.B.
二.填空题
11.22.5.
12.5.
13.15或60.
14.7.5.
15.45.
16.130cm.
三.解答题
17.(1)证明:∵BC=5,CD=4,BD=3,
∴42+32=52,
∴∠BDC=90°;
(2)解:在Rt△ADC中,∠ADC=180°﹣90°=90°,
依题意有AC2=(AB﹣3)2+CD2,即AC2=(AC﹣3)2+42,
解得AC.
故AC的长为.
18.解:取AB的中点O,过D作DE⊥AB于E,
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r(寸),DE=10寸,OECD=1寸,
∴AE=(r﹣1)寸,
在Rt△ADE中,
AE2+DE2=AD2,即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
答:门宽AB的长是101寸.
19.解:(1)在Rt△ABC中,由勾股定理得:BC4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
20.解:(1)∵CD2+AD2=144+81=225,AC2=225,
∴CD2+AD2=CA2,
∴△△ADC是直角三角形,
∴∠ADC=90°,
∴CD⊥AB,
∴∠ADC=90°,
∴BD16,
∴AB=AD+DB=16+9=25,
∴△ABC的面积25×12=150;
(2)过C作CD⊥BA的延长线于点D,
∵CD⊥AB,
∴∠CDB=90°,
设AD为x,DB=(x+11),由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣DB2,
即AC2﹣AD2=BC2﹣DB2,
则132﹣x2=202﹣(x+11)2,
解得:x=5,
∴CD12,
∴△ABC的面积 AB CD11×12=66.
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACDAB×ACAD×CD8×1512×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABCBC×AEAB AC,
∴17×AE=8×15,
解得:AE(m),
即小路AE的长为m.
22.解:(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.
23.解:(1)AC=BC且AC⊥BC.理由:
如图(1),∵CD=BE,∠ADC=∠CEB=90°,AD=CE,
∴△ACD≌△CBE(SAS),
∴AC=CB,∠ACD=∠CBE,
又∵∠CBE+∠BCE=90°,
∴∠ACD+∠BCE=90°,
∴∠ACB=180°﹣90°=90°,
∴AC⊥BC;
(2)如图(2),作△ABC,△DEF,
∵BC=FE,∠ABC=∠DFE,AB=DF,
∴△ABC △DFE(SAS),
∴∠ACB=∠DEF=∠2.
由图,结合勾股定理,得
,,AD=5,
∴AC2+DC2=5+20=25=AD2,
∴△ACD是直角三角形,且∠ACD=90°.
∵∠2+∠ACD+∠1=180°,
∴∠1+∠2=180°﹣∠ACD=180°﹣90°=90°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
