初中数学教学课件:27.1图形的相似(人教版九年级下)
文档属性
| 名称 | 初中数学教学课件:27.1图形的相似(人教版九年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-22 00:00:00 | ||
图片预览








文档简介
课件29张PPT。第二十七章 相似
27.1 图形的相似1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形概念;
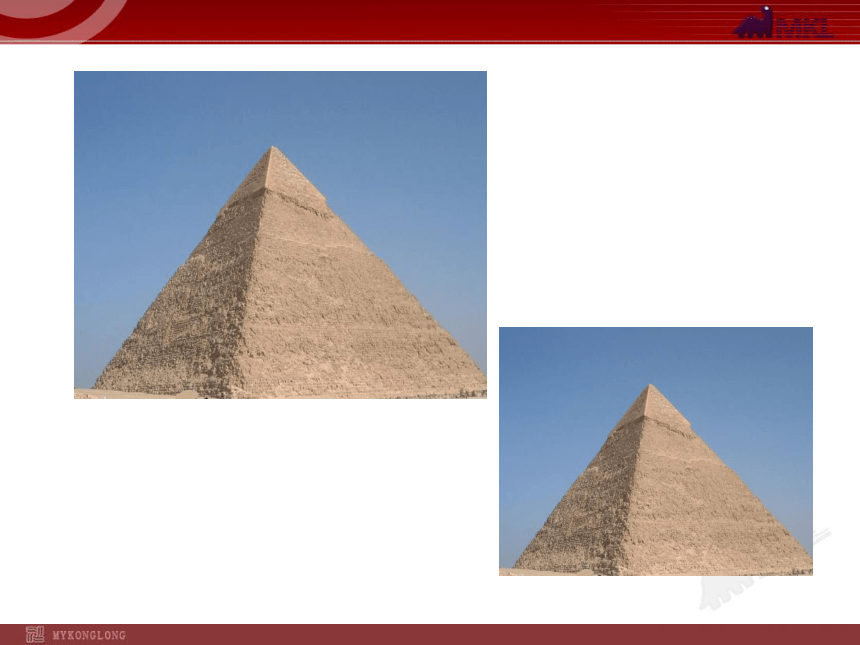
2.理解相似图形的性质和判定.请观察下面几组图片
你能发现它们有什么特点吗?形状相同,大小不一定相同我们把这些形状相同的图形叫做相似图形.我们把这些形状相同的图形叫做相似图形.两两相似的几何图形下图是人们从平面镜及哈哈镜里看到的不同镜像,
它们相似吗?观察下列图形,哪些是相似图形?观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)、(3)相似的?A B D F下列图形中____与_____是相似的.(1) (2) (3) (4)选一选(1) (4) 将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?对应角相等对应边的比相等对应角相等对应边的比相等能图(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边是否有同样的结论?对应角相等对应边的比相等有对应角相等对应边的比相等(1)(2)相似多边形对应边的比称为相似比相似多边形对应角相等,对应边的比相等.全等相似多边形的判断方法:若两个多边形满足对应角相等,对应边的比相等,则这两个多边形相似.相似多边形的性质:对于四条线段,a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.【例1】 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.DABC18cm21cm78°83°β24cmGEFHαx118°在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.∠α=∠C=83°,∠A=∠E=118°解析:四边形ABCD和EFGH相似,它们的对应角相等.
由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.
由此可得解得 x=28(cm)如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似?∴不相似1.(德化中考)下列各组线段(单位:㎝)中,
成比例线段的是( )
A.1、2、3、4 B.1、2、2、4
C.3、5、9、13 D.1、2、2、3B2.(南平中考)下列说法中,错误的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3.(烟台中考)手工制作课上,小红利用一些花布的边
角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等
边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花
边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几
何图形不相似的是( )CD4.在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.5. 如图所示的两个五边形相似,求未知边a、b、 c、d的长度.【解析】由图所示, 可知两图形的相似比为:b = 4.5a = 3c = 4d = 61. 经过这节课的学习,你有哪些收获?
2. 你想进一步探究的问题是什么?
27.1 图形的相似1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形概念;
2.理解相似图形的性质和判定.请观察下面几组图片
你能发现它们有什么特点吗?形状相同,大小不一定相同我们把这些形状相同的图形叫做相似图形.我们把这些形状相同的图形叫做相似图形.两两相似的几何图形下图是人们从平面镜及哈哈镜里看到的不同镜像,
它们相似吗?观察下列图形,哪些是相似图形?观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)、(3)相似的?A B D F下列图形中____与_____是相似的.(1) (2) (3) (4)选一选(1) (4) 将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?对应角相等对应边的比相等对应角相等对应边的比相等能图(1)是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边是否有同样的结论?对应角相等对应边的比相等有对应角相等对应边的比相等(1)(2)相似多边形对应边的比称为相似比相似多边形对应角相等,对应边的比相等.全等相似多边形的判断方法:若两个多边形满足对应角相等,对应边的比相等,则这两个多边形相似.相似多边形的性质:对于四条线段,a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.【例1】 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.DABC18cm21cm78°83°β24cmGEFHαx118°在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.∠α=∠C=83°,∠A=∠E=118°解析:四边形ABCD和EFGH相似,它们的对应角相等.
由此可得 四边形ABCD和EFGH相似,它们的对应边的比相等.
由此可得解得 x=28(cm)如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似?∴不相似1.(德化中考)下列各组线段(单位:㎝)中,
成比例线段的是( )
A.1、2、3、4 B.1、2、2、4
C.3、5、9、13 D.1、2、2、3B2.(南平中考)下列说法中,错误的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3.(烟台中考)手工制作课上,小红利用一些花布的边
角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等
边三角形、等边三角形、正方形、矩形花边框,其中,每个图案花
边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几
何图形不相似的是( )CD4.在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离.5. 如图所示的两个五边形相似,求未知边a、b、 c、d的长度.【解析】由图所示, 可知两图形的相似比为:b = 4.5a = 3c = 4d = 61. 经过这节课的学习,你有哪些收获?
2. 你想进一步探究的问题是什么?
