周期现象
图片预览





文档简介
课件14张PPT。为什么学习三角函数? 自然界中存在大量的周期现象,为了研究周期现象中蕴涵的数学规律,我们才学习三角函数。
三角函数是描述客观世界中周期性变化规律的重要数学模型,有着广泛的实践意义和理论价值。它是我们高中阶段学习的又一类重要的初等函数。§1 周期现象思考:
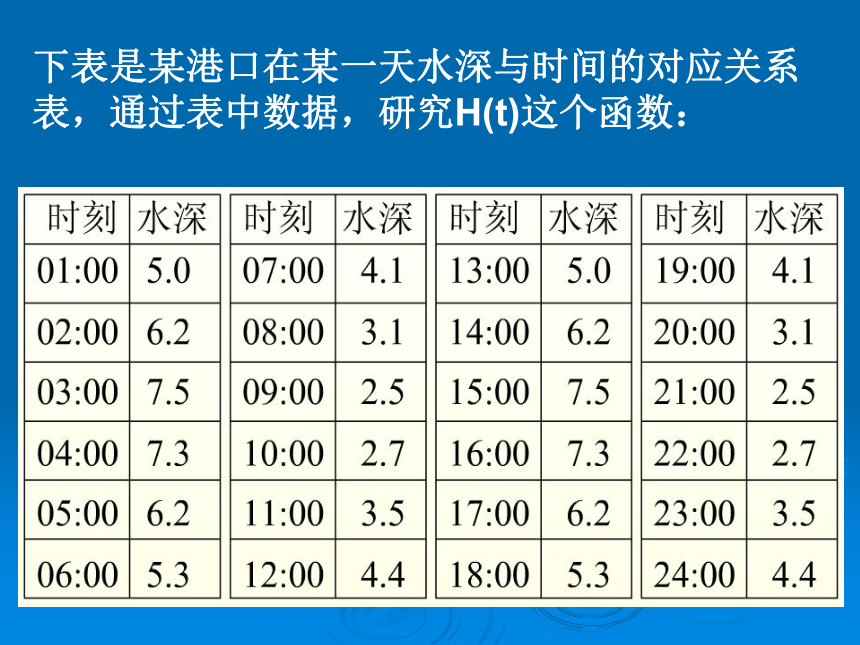
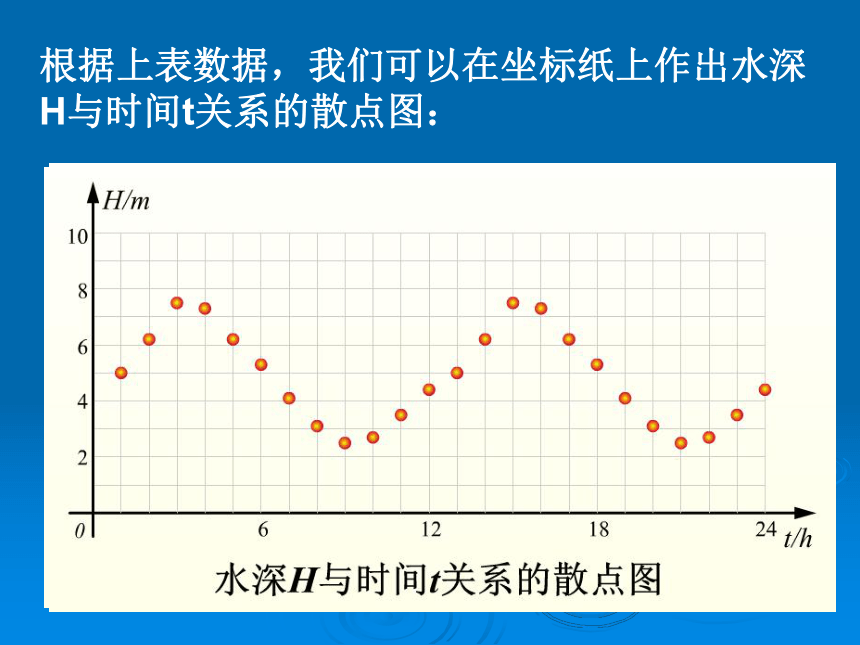
什么是周期现象?请大家举例说明。潮汐现象:海水大约每一昼夜的时间里,潮水会涨落两次,因此潮汐现象也是周期现象.思考:若确定一个位置,考察该位置的水深H和时间 t 的关系,那么H是 t 的函数吗? 由于一个时间 t 只对应唯一一个海水深度H,所以H是关于t的一个函数.下表是某港口在某一天水深与时间的对应关系表,通过表中数据,研究H(t)这个函数:根据上表数据,我们可以在坐标纸上作出水深H与时间t关系的散点图:抽象概括:
对于函数 y=f(x),如果存在不为0的实数T,使得对于定义域内的每一个x都有
f(x)=f(x+T),
称这种函数为“周期函数”,T为周期.其中,正周期中的最小数T,称为最小正周期例如:潮汐现象的函数H(t)中,12h、24h、36h都是一个周期,但是最小的是12h,所以这函数H(t)的最小正周期是12h.试判断下列现象是否属于周期现象。如果是,请指出最小正周期:(1)地球上一年春、夏、秋、冬四季的变化(2)钟表的分针的运动(3)连续抛一枚硬币,出现正面向上探究一:
地球围绕着太阳转,地球到太阳的距离y是时间t的函数吗? 这个函数y=f (t) 是不是周期函数?若是,指出最小正周期。探究二:
下图是钟摆示意图,摆心A到铅垂线MN的距离y是时间t的函数,即y=g(t)探究三:
我们选定自行车车轮边缘上一点A,的中心记为O,OA与竖直方向的夹角记为α(0o≤α<360o) .当自行车沿直线做匀速运动时,变量α是时间 t 的函数吗?探究四:
下图是水车示意图,水车上A点到水面的距离y是时间t的函数,即y=g(t)思考交流1、在潮汐函数中,若已知H(4.5)=6.8,你能否估计H(16.5)=?2、若周期函数f(x)是奇函数,6是f(x)的一个周期,且f(-1)=2,则f(1)是多少?f(-5)又是多少?课后作业习题1.1
第1、2、3题
三角函数是描述客观世界中周期性变化规律的重要数学模型,有着广泛的实践意义和理论价值。它是我们高中阶段学习的又一类重要的初等函数。§1 周期现象思考:
什么是周期现象?请大家举例说明。潮汐现象:海水大约每一昼夜的时间里,潮水会涨落两次,因此潮汐现象也是周期现象.思考:若确定一个位置,考察该位置的水深H和时间 t 的关系,那么H是 t 的函数吗? 由于一个时间 t 只对应唯一一个海水深度H,所以H是关于t的一个函数.下表是某港口在某一天水深与时间的对应关系表,通过表中数据,研究H(t)这个函数:根据上表数据,我们可以在坐标纸上作出水深H与时间t关系的散点图:抽象概括:
对于函数 y=f(x),如果存在不为0的实数T,使得对于定义域内的每一个x都有
f(x)=f(x+T),
称这种函数为“周期函数”,T为周期.其中,正周期中的最小数T,称为最小正周期例如:潮汐现象的函数H(t)中,12h、24h、36h都是一个周期,但是最小的是12h,所以这函数H(t)的最小正周期是12h.试判断下列现象是否属于周期现象。如果是,请指出最小正周期:(1)地球上一年春、夏、秋、冬四季的变化(2)钟表的分针的运动(3)连续抛一枚硬币,出现正面向上探究一:
地球围绕着太阳转,地球到太阳的距离y是时间t的函数吗? 这个函数y=f (t) 是不是周期函数?若是,指出最小正周期。探究二:
下图是钟摆示意图,摆心A到铅垂线MN的距离y是时间t的函数,即y=g(t)探究三:
我们选定自行车车轮边缘上一点A,的中心记为O,OA与竖直方向的夹角记为α(0o≤α<360o) .当自行车沿直线做匀速运动时,变量α是时间 t 的函数吗?探究四:
下图是水车示意图,水车上A点到水面的距离y是时间t的函数,即y=g(t)思考交流1、在潮汐函数中,若已知H(4.5)=6.8,你能否估计H(16.5)=?2、若周期函数f(x)是奇函数,6是f(x)的一个周期,且f(-1)=2,则f(1)是多少?f(-5)又是多少?课后作业习题1.1
第1、2、3题
