角的概念的推广

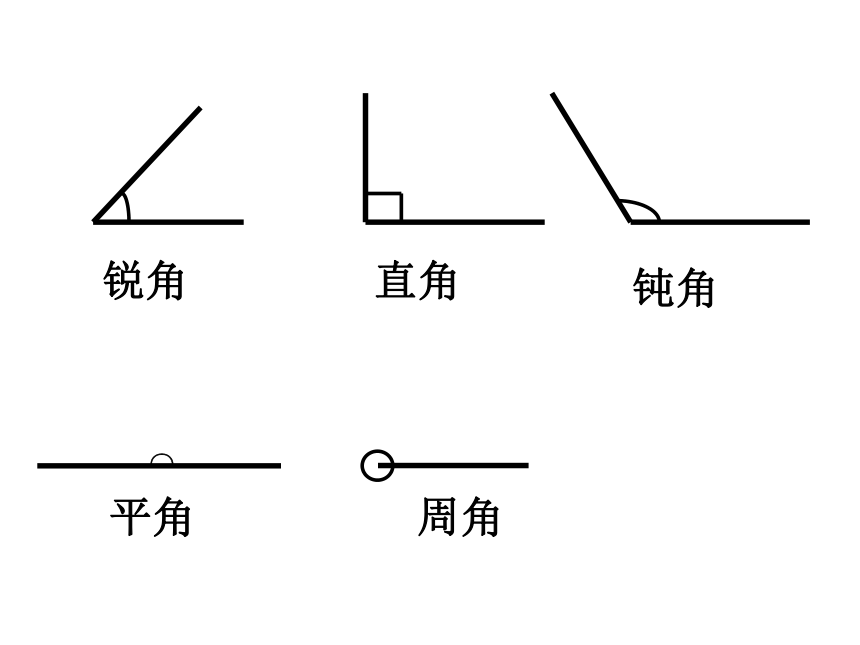
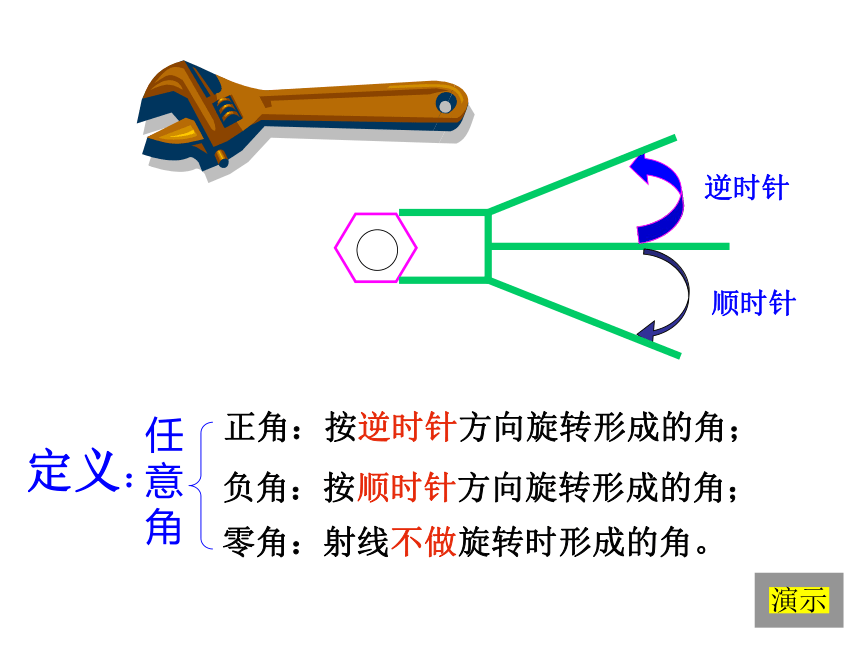
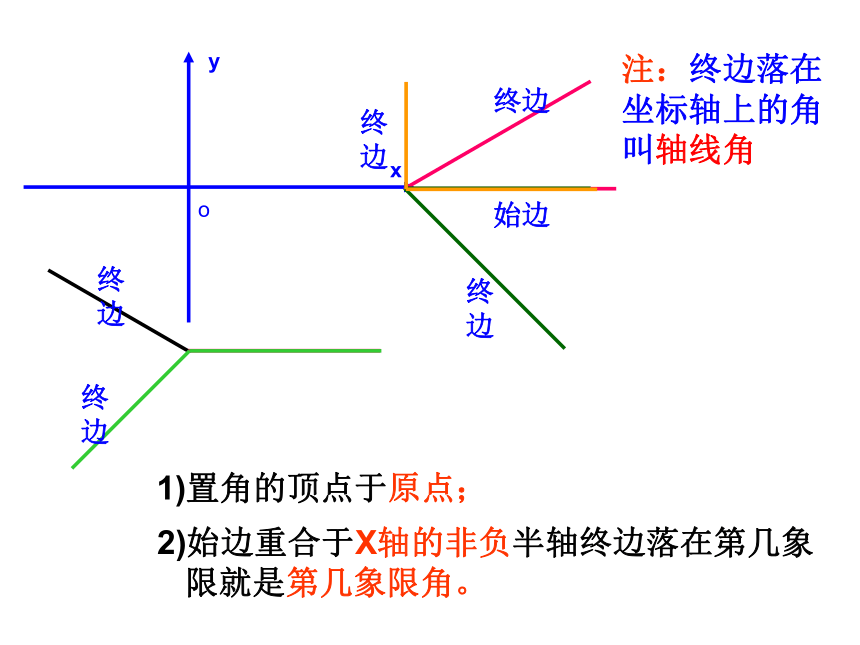
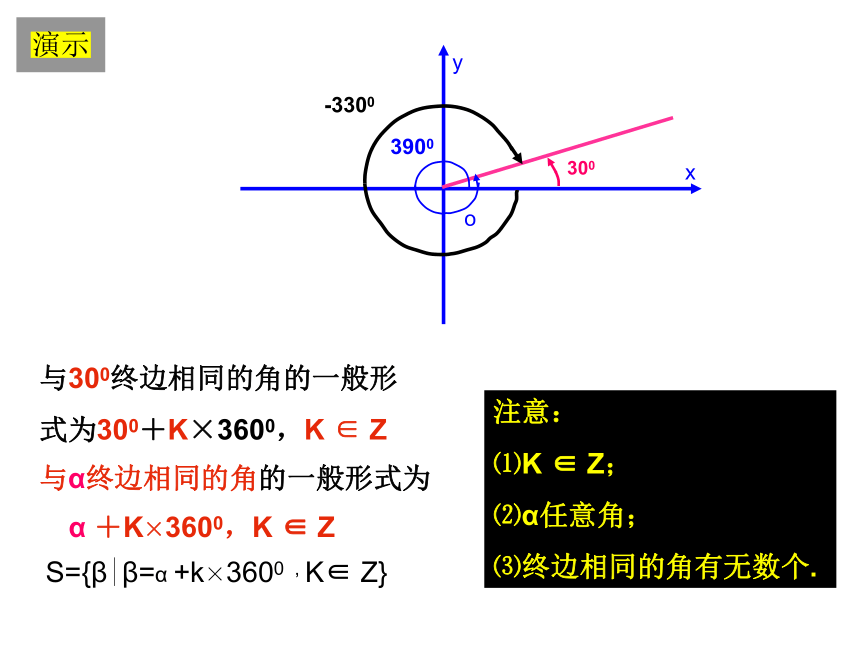
课件15张PPT。§1.2 角的概念的推广新课引入G S P锐角直角钝角平角周角╭╮ 逆时针 顺时针定义：正角：按逆时针方向旋转形成的角；负角：按顺时针方向旋转形成的角；　零角：射线不做旋转时形成的角。任意角演示任意角：正角负角零角xyo1)置角的顶点于原点；2)始边重合于X轴的非负半轴终边落在第几象 限就是第几象限角。注：终边落在坐标轴上的角叫轴线角3003900-3300与300终边相同的角的一般形
式为300＋K×3600，K ∈ Z与α终边相同的角的一般形式为α ＋K×3600，K ∈ ZS={β|β=α +k×3600 , K∈ Z}注意：
⑴K ∈ Z；
⑵α任意角；
⑶终边相同的角有无数个.演示｛α|α=β+k × 3600,k∈Z｝2、判断
（1）始边、终边相同的角一定相等。 （ ）
（2）始边、终边相同的角有无数个，它们彼此相差
的3600整数倍。 （ ）
（3）始边相同，而且相等的角终边一定相同。（ ）例1、把下列各角写成α+ k×3600（00≤α＜3600,ｋ∈Z）的形式，并判定它们分别是第几象限角：(1) 1990°12′; (2) －1998°；解 : (1) 因为1990°12′＝190°12′＋5×360°190°12′是与1990°12′终边相同的角因为190°12′是第三象限的角，所以1990°12′是第三象限的角。(2) 因为－1998°＝162°+(－6)×360°－1998°是与162°终边相同的角所以－1998°是第二象限的角。判断角的象限方法
1.写成α+k×3600（00≤α＜3600,ｋ∈Z）的形式; 2.由α的象限得出结论.例2、写出终边落在坐标轴上的角的集合。终边落在坐标轴上的情形0°90°180°270° +k·360°+k·360°+k·360°+k·360°或360°＋k·360°例3、写出终边落在y轴上的角的集合。解：终边落在ｙ轴非负半轴上的角的集合为S1={β|β=90°+K?360°,K∈Z} ={β|β=90°+2K?180°,K∈Z}={β| β=90°+180° 的偶数倍}终边落在ｙ轴非正半轴上的角的集合为S2={β| β=270°+K?360°,K∈Z}={β| β=90°+180°+2K?180°,K∈Z}={β| β=90°+（2K+1）180° ,K∈Z}={β| β=90°+180° 的奇数倍}S=S1∪S2所以，终边落在ｙ轴上的角的集合为={β| β=90°+180°的偶数倍}∪{β|β=90°+180°的奇数倍}={β|β=90°+180°的整数倍}　　={β|β=90°+K?180°,K∈Z}{偶数}∪{奇数}={整数}练习1、写出终边落在x轴上的角的集合。解：终边落在x轴非负半轴上的角的集合为S1={β|β= K?360°,K∈Z} ={β| β= 2K?180°,K∈Z} ={β| β= 180°的偶数倍}终边落在x轴负半轴上的角的集合为S2={β| β=180°+ K?360°,K∈Z}={β| β= 180°+ 2K?180°,K∈Z}={β| β=(2K+1)180° ,K∈Z}={β| β= 180°的奇数倍}S=S1∪S2所以，终边落在 x 轴上的角的集合为={β| β=180° 的整数倍}　={β| β=K?180° ，K∈Z}{偶数}∪{奇数}＝{整数}例4、写出与下列各角的始边、终边相同的角的集合,以及其中-3600 ~7200之间的角： （1）600 （2）-500解：(1) 与600角始边、终边相同的角的集合是：｛α|α= 600 +k × 3600,k∈Z｝其中在-3600 ~7200之间的角是：600 +0× 3600= 600600 +1× 3600= 4200600 +（-1）× 3600= -3000(2)与-500角始边、终边相同的角的集合是：｛α|α= -500 +k × 3600,k∈Z｝其中在-3600 ~7200之间的角是：-500 +1× 3600= 3100-500 +2× 3600= 6700-500 +0× 3600= -500小结：1.任意角的概念正角：射线按逆时针方向旋转形成的角负角：射线按顺时针方向旋转形成的角零角：射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角3)终边落在第几象限就是第几象限角3.终边与角α相同的角α＋K·360°，K∈Z习题1.2
第2、3题课后作业