人教A版(2019)选择性必修第二册 4.3.1等比数列的概念及通项公式 课件(共33张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第二册 4.3.1等比数列的概念及通项公式 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 992.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
第四章 数列
4.3.1等比数列的概念
及通项公式(1)
共同特点:
从第二项起,每一项与前一项的比都等于同一个常数.
课堂探究
观察,并说出它们的运算特点.
(1)…
(2)…
(3)…
(4)
(5)。
(6)1,2,4,8,16,32,…
等比数列的定义
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列. 这个常数叫做等比数列的公比,通常用字母 q 表示(显然q ≠ 0).
等比数列通项公式的理解
(1)已知首项a1和公比 q,可以确定一个等比数列.
(2)对于等比数列{an},
若q>0,则数列{an}各项同号;
若q<0,则{an}中正负项间隔出现.
...
概念辨析
思考:2 , 2 , 2 ,…是等比数列?
思考:0 , 0, 0 ,…是等比数列?
思考:2 , 0, 2,0,…是等比数列?
是等比数列 首项是2,公比是1
不是等比数列
不是等比数列
结论:1、常数列一定是等差数列
2、 任意项不为零的常数列是等比数列
课堂探究
类比等差数列,在如下的两个数之间,插入一个什么数后这三个数就会成为一个等比数列:
(1) 2,( ),8
(2) -12,( ),-3
4或-4
6或-6
由三个数a,A,b组成的等比数列可以看成是最简单的等比数列.这时,A叫做a与b的等比中项且A2=a+b.
【思考】下列所给的两个数之间,插入一个什么数后三个数就会成为一个等比数列:(1)2,4;(2)-1,-5;(3)3,27;(4)a,b(a,b不为0).
例题解析
例2:如果-1,a,b,c,-9成等比数列,
那么b=_____,ac=___.
【解析】因为b是-1,-9的等比中项,
所以b2=9,b=±3.
又等比数列奇数项符号相同,得b<0,故b=-3,
而b又是a,c的等比中项,
故b2=ac,即ac=9.
首项为a1, 公差为q的等比数列{an}的通项公式为
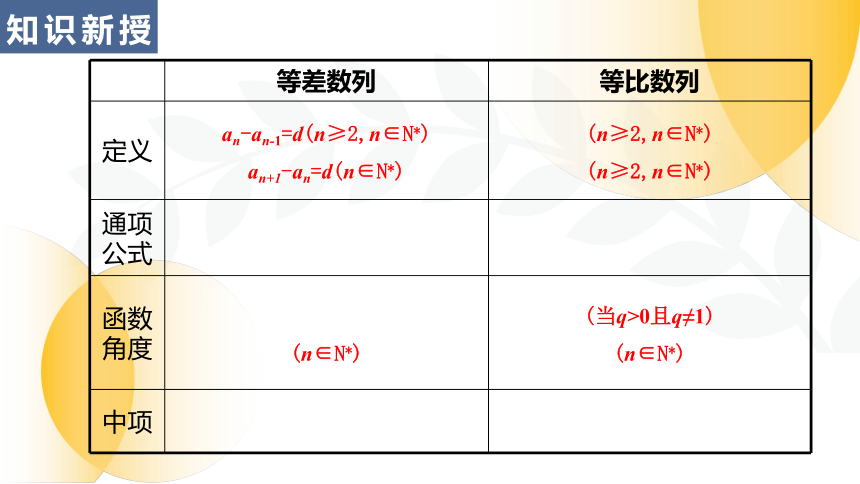
知识新授
等差数列 等比数列
定义 an-an-1=d(n≥2,n∈N*) an+1-an=d(n∈N*) (n≥2,n∈N*)
(n≥2,n∈N*)
通项公式
函数角度 (n∈N*) (当q>0且q≠1)
(n∈N*)
中项
例题解析
例1:在等比数列{an}中:
(1)a1=1,a4=8,求an;
(2)an=625,n=4,q=5,求a1;
(3)a2+a5=18,a3+a6=9,an=1,求n.
【解析】(1)a4=a1q3,
8=q3,所以q=2,an=a1qn-1=2n-1.
(2),
例题解析
例1:在等比数列{an}中:
(1)a1=1,a4=8,求an;
(2)an=625,n=4,q=5,求a1;
(3)a2+a5=18,a3+a6=9,an=1,求n.
【解析】(3),两式相除可得
,又,
,.
1.在等比数列{an}中,
(1)若 , ,求an;
(2)若 , ,求an.
解:(1)设等比数列{an}的公比为q,
由题 解得 ,
∴{an}的通项公式是 .
(2)设等比数列{an}的公比为q,
由题 解得 或
∴{an}的通项公式是 或 .
即 或 .
第四章 数列
4.3.1等比数列的概念
及通项公式(2)
等比数列的判定
例1.已知数列{an}中,a1=2,an+1=2an-1. 判断数列{an-1}是否为等比数列?并说明理由.
解析:数列 是等比数列.
证明如下:
∵ , ,
∴
∴数列 是以1为首项,公比为2的等比数列.
1.已知数列{an}的前n项和Sn=2an+1,试判断数列{an}是否是等比数列?
解:∵ ,∴ ,
作差得
∴ ,
又 ,∴
∴数列{an}是以-1为首项,公比为2的等比数列.
反思感悟 巧设等差数列、等比数列的方法
(1)若三个数成等差数列,则常设成a-d,a,a+d.若三个数成等比数列,则常设成 ,a,aq或a,aq,aq2.
例2.已知三个正数成等比数列,它们的积为27,它们的平方和为91,求这三个数.
解析:法一:设这三个数依次为 , ,
由题意知 ,
所以
化简得
即 ,解得 或
又三个数为正数,故 或
当 时, ,这三个数依次为1,3,9;
当 时, ,这三个数依次为9,3,1.
法二:设这三个数依次为 , , ,
由题意知 ,
化简得 ,解得 或
又三个数为正数,故 或
当 时, ,这三个数依次为1,3,9;
当 时, ,这三个数依次为9,3,1.
1、有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
解:
第四章 数列
4.3.1等比数列的概念
及通项公式(3)
(4){anm}(m是整数常数)是公比为qm的等比数列;
(5){|an|}是公比为|q|的等比数列;
等比数列的性质
若数列{an}是公比为q 的等比数列,则
① ;
②若 ,则 ;
特别地,若 ,则 ;
1:在等比数列 中,
(1)已知 , 则公比q的值为________
(2)已知 ,则
2、已知等比数列{an}中,a2·a4·a6·a8=16,则a3·a7等于 ( )
A.±4 B.4 C.8 D.±8
B
C
例1.(1)在等比数列{an}中,若a3=2,a7=12,则a11=________.
(2)在等比数列{an}中,若a10=-2,则此数列的前19项之积等于______.
解析:(1)由等比数列的性质,有 ,
所以 .
(2)因为 ,
所以 .
1.已知数列{an}是等比数列,
(1)若a2a6a10=27,求a3·a9的值;
(2)若a1+a2+a3=7,a1a2a3=8,求数列{an}的通项公式.
解析:(1)由等比数列的性质,有 ,
所以 ,得 ,
则 .
(2)由等比数列的性质,有 ,
所以 ,得 ,
又 ,所以 ,
即 ,化简得 ,
解得 或 ,
所以 或 ,则 或 .
第四章 数列
4.3.1等比数列的概念
及通项公式(1)
共同特点:
从第二项起,每一项与前一项的比都等于同一个常数.
课堂探究
观察,并说出它们的运算特点.
(1)…
(2)…
(3)…
(4)
(5)。
(6)1,2,4,8,16,32,…
等比数列的定义
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列. 这个常数叫做等比数列的公比,通常用字母 q 表示(显然q ≠ 0).
等比数列通项公式的理解
(1)已知首项a1和公比 q,可以确定一个等比数列.
(2)对于等比数列{an},
若q>0,则数列{an}各项同号;
若q<0,则{an}中正负项间隔出现.
...
概念辨析
思考:2 , 2 , 2 ,…是等比数列?
思考:0 , 0, 0 ,…是等比数列?
思考:2 , 0, 2,0,…是等比数列?
是等比数列 首项是2,公比是1
不是等比数列
不是等比数列
结论:1、常数列一定是等差数列
2、 任意项不为零的常数列是等比数列
课堂探究
类比等差数列,在如下的两个数之间,插入一个什么数后这三个数就会成为一个等比数列:
(1) 2,( ),8
(2) -12,( ),-3
4或-4
6或-6
由三个数a,A,b组成的等比数列可以看成是最简单的等比数列.这时,A叫做a与b的等比中项且A2=a+b.
【思考】下列所给的两个数之间,插入一个什么数后三个数就会成为一个等比数列:(1)2,4;(2)-1,-5;(3)3,27;(4)a,b(a,b不为0).
例题解析
例2:如果-1,a,b,c,-9成等比数列,
那么b=_____,ac=___.
【解析】因为b是-1,-9的等比中项,
所以b2=9,b=±3.
又等比数列奇数项符号相同,得b<0,故b=-3,
而b又是a,c的等比中项,
故b2=ac,即ac=9.
首项为a1, 公差为q的等比数列{an}的通项公式为
知识新授
等差数列 等比数列
定义 an-an-1=d(n≥2,n∈N*) an+1-an=d(n∈N*) (n≥2,n∈N*)
(n≥2,n∈N*)
通项公式
函数角度 (n∈N*) (当q>0且q≠1)
(n∈N*)
中项
例题解析
例1:在等比数列{an}中:
(1)a1=1,a4=8,求an;
(2)an=625,n=4,q=5,求a1;
(3)a2+a5=18,a3+a6=9,an=1,求n.
【解析】(1)a4=a1q3,
8=q3,所以q=2,an=a1qn-1=2n-1.
(2),
例题解析
例1:在等比数列{an}中:
(1)a1=1,a4=8,求an;
(2)an=625,n=4,q=5,求a1;
(3)a2+a5=18,a3+a6=9,an=1,求n.
【解析】(3),两式相除可得
,又,
,.
1.在等比数列{an}中,
(1)若 , ,求an;
(2)若 , ,求an.
解:(1)设等比数列{an}的公比为q,
由题 解得 ,
∴{an}的通项公式是 .
(2)设等比数列{an}的公比为q,
由题 解得 或
∴{an}的通项公式是 或 .
即 或 .
第四章 数列
4.3.1等比数列的概念
及通项公式(2)
等比数列的判定
例1.已知数列{an}中,a1=2,an+1=2an-1. 判断数列{an-1}是否为等比数列?并说明理由.
解析:数列 是等比数列.
证明如下:
∵ , ,
∴
∴数列 是以1为首项,公比为2的等比数列.
1.已知数列{an}的前n项和Sn=2an+1,试判断数列{an}是否是等比数列?
解:∵ ,∴ ,
作差得
∴ ,
又 ,∴
∴数列{an}是以-1为首项,公比为2的等比数列.
反思感悟 巧设等差数列、等比数列的方法
(1)若三个数成等差数列,则常设成a-d,a,a+d.若三个数成等比数列,则常设成 ,a,aq或a,aq,aq2.
例2.已知三个正数成等比数列,它们的积为27,它们的平方和为91,求这三个数.
解析:法一:设这三个数依次为 , ,
由题意知 ,
所以
化简得
即 ,解得 或
又三个数为正数,故 或
当 时, ,这三个数依次为1,3,9;
当 时, ,这三个数依次为9,3,1.
法二:设这三个数依次为 , , ,
由题意知 ,
化简得 ,解得 或
又三个数为正数,故 或
当 时, ,这三个数依次为1,3,9;
当 时, ,这三个数依次为9,3,1.
1、有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
解:
第四章 数列
4.3.1等比数列的概念
及通项公式(3)
(4){anm}(m是整数常数)是公比为qm的等比数列;
(5){|an|}是公比为|q|的等比数列;
等比数列的性质
若数列{an}是公比为q 的等比数列,则
① ;
②若 ,则 ;
特别地,若 ,则 ;
1:在等比数列 中,
(1)已知 , 则公比q的值为________
(2)已知 ,则
2、已知等比数列{an}中,a2·a4·a6·a8=16,则a3·a7等于 ( )
A.±4 B.4 C.8 D.±8
B
C
例1.(1)在等比数列{an}中,若a3=2,a7=12,则a11=________.
(2)在等比数列{an}中,若a10=-2,则此数列的前19项之积等于______.
解析:(1)由等比数列的性质,有 ,
所以 .
(2)因为 ,
所以 .
1.已知数列{an}是等比数列,
(1)若a2a6a10=27,求a3·a9的值;
(2)若a1+a2+a3=7,a1a2a3=8,求数列{an}的通项公式.
解析:(1)由等比数列的性质,有 ,
所以 ,得 ,
则 .
(2)由等比数列的性质,有 ,
所以 ,得 ,
又 ,所以 ,
即 ,化简得 ,
解得 或 ,
所以 或 ,则 或 .
