平均数

《平 均 数》
海南省国兴中学 陈香茹
1.教材分析
1.1本节课所处的地位作用：
本节课选自义务教育课程标准实验教科书《数学》（北师大版）八年级上册第八章“数据的代表”第一节《平均数》(第一课时)．主要内容是算术平均数、加权平均数的概念及计算．"统计与概率"是中小学数学课程的重要内容，在义务教育阶段占有重要的位置．本节课是在小学学习的基础上，进一步认识生活中刻画“平均水平” 的三个数据代表之一——平均数．平均数是人们对数据加工处理和作出评判的常用指标．学生通过学习本节内容加深了对生活中常用数据的认识，学会分析、处理数据并且能够作出合理决策，同时为以后进一步学习统计知识提供基础．
1.2教学目标
根据《数学课程标准》提出的要求，结合八年级学生认知发展水平和已有的知识经验基础，我从以下三个方面确定教学目标：
1.2.1知识与技能
a．掌握算术平均数、加权平均数的概念．
b．会求一组数据的算术平均数、加权平均数．
1.2.2过程与方法
a．初步经历数据的收集与处理的过程，发展学生初步的统计意识和数据处理能力．
b．根据有关平均数问题的解决，培养学生的判断能力．
1.2.3情感态度价值观
a．通过小组合作的活动，培养学生的合作意识和能力．
b．通过解决身边的实际问题，让学生初步认识数学与人类生活的密切联系．
1.3教学重点与难点：
教学重点为：a．掌握算术平均数、加权平均数的概念．
b．会求一组数据的算术平均数、加权平均数．
教学难点为：理解加权平均数的“权”，会求一组数据的加权平均数．
2.教学设计：
教学环节 教 学 程 序 设 计 意 图
教 师 活 动 学生活动
2.1导入设计2.1导入设计 一、本章导入生活中，人们离不开数据．作为学生最熟悉的数据是自己的学习成绩，因此我以我们班最近两次数学测试统计表作为整章的导入． 在这个背景下，教师提出问题：“你能从表中读出哪些信息？”这个问题并不要求学生作出完整的回答，只要他们说得有道理都给于肯定．比如学生容易观察到哪个分数段的人数最多或最少，成绩相对集中在哪些分数段．对于学生疑惑的问题先不给出定性的结论．告诉他们学习了这章知识，相信大家就会有比较满意的答案．二、本节导入平均数是人们对数据加工处理和作出评判的常用指标．这节课我们先来学习生活中常用来“刻画平均水平”的数据代表之一——“平均数”．接着我就展示NBA火箭队和雄鹿队篮球比赛的精彩片段导入本节课的内容，并提出以下问题：1.影响篮球比赛成绩的主要因素有哪些？ 在与学生讨论之后给出第二个问题．2.怎样理解“甲队队员的身高比乙队更高”？先让学生发表个人看法，教师再进一步引导，并给出第三个问题．3.要比较两个球队队员的身高，需要收集哪些数据？ 观察……思考……讨论……学生议论：有心理因素、大伙配合程度、有技术成分、还有身高和年龄等因素．分别求出两个球队队员的身高，然后再作比较．需要收集每队各个队员的身高． 这里从学生熟悉的问题入手，让学生感受数据的普遍存在和收集、处理、分析数据的必要性．选这两支球队是因为有我们中国篮坛的两位球星在里面，学生比较熟悉和喜欢他们，这样能激发学生学习的积极性．问题1打开学生的思路，让学生在轻松的氛围中进入本节课的学习．问题2是在问题1的基础上产生出来的，它引发学生思考日常生活中一些判断的含义和依据，激发学生的学习兴趣．这里有的学生可能会认为最高球员在哪个队，那个队队员的身高就比另一个队的高．在这种情况下老师就要引导学生不能单看一个人的情况，要从整体比较，从而要用平均数来衡量．这样就自然过渡到我们这节课的重点．问题3让学生明确收集数据的必要性．
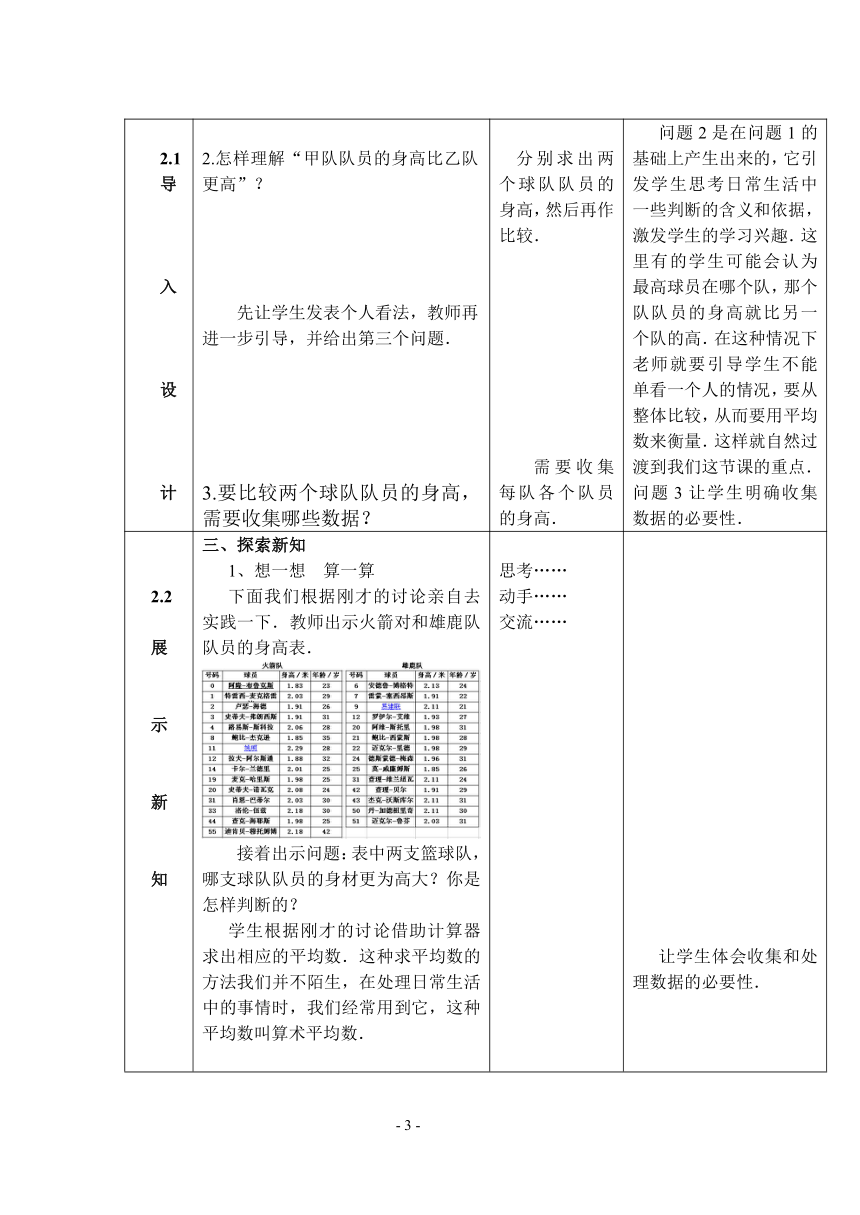
2.2展示新知2.2展示新知 三、探索新知1、想一想 算一算下面我们根据刚才的讨论亲自去实践一下．教师出示火箭对和雄鹿队队员的身高表．接着出示问题：表中两支篮球队，哪支球队队员的身材更为高大？你是怎样判断的？学生根据刚才的讨论借助计算器求出相应的平均数．这种求平均数的方法我们并不陌生，在处理日常生活中的事情时，我们经常用到它，这种平均数叫算术平均数．2、平均数概念出示算术平均数的定义：一般地，对于n个数，，…，，我们把叫做这n个数的算术平均数（mean），简称平均数，记，读作“x拔”．3、想一想现在我们根据算术平均数的定义再去计算下面的问题：给出NBA火箭队和雄鹿队的年龄表和问题：哪支球队队员年龄更小？你是怎样判断的？在学生思考、讨论、动手完成的基础上，我根据学生的情况给出小丽的错误算法，让学生讨论、判断，从而得出和小明一样的正确算法．小丽的算法：(21+22+24+26+27+28+29+30+31+34)＝27.2(岁）小明的算法：≈27.215（岁） 思考……动手……交流……火箭队的平均身高为： （1.83+2.03+…+2.18)=2.01（米）雄鹿队的平均身高为： (2.13+1.91+…+2.03) = 2.01（米）火箭队的平均年龄＝(23+29+…+ 42) ÷15=29（岁）雄鹿队的平均年龄＝ (24+22+…+31) ÷14=27（岁）学生讨论、判断 让学生体会收集和处理数据的必要性．算术平均数的概念把学生已经学习过的平均数及其算法进行巩固、提高、升华．计算平均年龄既能巩固所学内容，又能自然过渡到“加权平均数”新内容．通过小丽与小明的两种算法引起学生的争议，教师进一步引导学生对平均数的深入理解．小丽的算法给出了学生在求平均数时常出现的一种错误算法，让学生更好的体会平均数的含义．小明的算法让学生从算术平均数过渡到加权平均数，为学生理解加权平均数的“权”构建一个“台阶”，达到分散难点的目的．
2.3范例教学 4、想一想 议一议例1 某广告公司欲招聘广告策划人员一名，对A，B，C三名候选人进行了三项素质测试．他们的各项测试成绩如下表所示：测试项目测试成绩ABC创新728567综合知识507470语言884567
首先给学生提出以下问题：（1）根据测试成绩，假设你是该公司经理，你将录用谁？ 教师先让学生讨论，并发表个人见解．学生的答案是多样的，有的想到录用A，因为总分最高；有的想到录用C，因为各成绩较“平衡”；有的想到录用B，因为其“创新”科目成绩最好．教师根据学生的回答给予肯定并引导学生学会分析与处理数据、学会运用数据信息做出合理的决策．这里要招聘的是“广告策划人员”，当然创新知识最重要，自然过渡到“加权平均数”．接着提出第二个问题：（2）如果根据三项测试的平均成绩录用人选，那么谁将被录用？（3）根据实际需要，公司将创新、综合知识和语言三项测试得分按4：3：1的比例确定各人的测试成绩，此时谁将被录用？问题（3）在学生充分思考和讨论的基础上，我是这样引导学生的：得分按4:3:1说明它们的重要程度不同，类比小明刚才的算法，这里我们可以理解为“创新”出现４次，“综合知识”出现３次，而“语言”出现１次，从而得出三人的相应成绩．根据学生掌握情况，如果学生理解有困难时，教师再从另外一个角度解释：比分按4：3：1说明将总体等分成（4+3+1）=8（份），“创新”占总体的4份，“综合知识”占3份，“语言”占1份．从而得出三人的相应成绩． 议一议（2）（3）结果不一样说明了什么？5、加权平均数的概念在实际问题中，一组数据里的“重要程度”未必相同．因而，在计算这组数据的平均数时，往往给每个数据加一个“权”．例1中的4，3，1分别是创新、综合知识、语言三项测试成绩的权（weight），而称为A的三项测试成绩的加权平均数（weighted mean） 独立思考，再小组交流完成．生1：录用A，因为总分最高；生2：录用C，因为各成绩较“平衡”；生3：录用B，因为其“创新”科目成绩最好．……学生动手计算问题（2）A的平均成绩为（72+50+88）÷3=70（分）B的平均成绩为（85+74+45）÷3=68（分）C的平均成绩为（67+70+67）÷3=68（分）因此候选人A将被录用．问题（3）A的测试为=65.75（分）B的测试成绩为=75.875（分）C的测试成绩为=68.125（分）因此候选人B被录用．议一议：因为在（2）中没有指出三项所占的比份，是把他们平等对待的；在（3）中规定了这三项所占的比份是4、3、1，所以（2）（3）结果就不一样．说明所占的比份不同对平均数有影响． 问题1让学生通过分析数据并尝试作出决策．问题2让学生巩固算术平均数的算法．问题3的设计是为了引出“加权平均数”的概念．同时让学生体会到学习“加权平均数”的必要性和重要性．通过议一议的解决引发学生思考重要性的差异对结果（平均数）的影响．
2.4反馈练习 四、反馈练习某次体操比赛，六位评委对某选手的打分如下（单位：分）9.8，9.3，8.8，9.5，9.4，9.3.（1）求这六个分数的平均分．（2）如果规定：去掉一个最高分和一个最低分，余下分数的平均值作为选手的最后得分．那么该选手的最后得分是多少？2.某校规定学生的体育由三部分组成：早锻炼及体育课外活动表现占成绩的20%，体育理论测试占30%，体育技能测试占50%．小颖的上述三项成绩依次是92分，80分，84分，则小颖这学期的体育成绩是多少？3.某条小河平均水深1.3米，一个身高1.6米的少年在这条河里游泳是否一定没有危险？ 独立思考再小组交流 练习1是让学生初步感受平均数受数据中的极端值的影响较大，同时加深对算术平均数的认识． 练习2是让学生巩固加权平均数的算法．练习3是让学生进一步体会平均数的含义，并进行安全教育．
2.5回顾小结 五、回顾小结掌握算术平均数、加权平均数的概念会求一组数据的算术平均数、加权平均数． 学生交流合作，师生共同小结． 检测本节课的学习效果，培养学生归纳问题、总结问题的能力，突出学生的主体地位．
2.6留下悬念 六、留下悬念八年级一班共有46人，学生的平均身高是1.58米，小明的身高是1.59米，但是小明说他的身高在全班是中等偏下的，班上有25个同学比他高，20个同学比他矮，这可能吗？请与同伴交流．某学校对各个班级的教室卫生情况的考察包括一下几项：黑板、门窗、桌椅、地面．一天，三个班级的各项卫生成绩分别如下：黑板门窗桌椅地面一班95909085二班90958590三班85909590你认为上述四项中，哪一项更为重要？请你按照自己的想法设计一个评分方案，哪一个班的卫生成绩最高？与同伴交流． 课后思考交流 问题1是让学生感受有时平均数并不能代表一组数据的特征，为学习众数、中位数作好铺垫．问题2是再一次让学生感受加权平均数在生活中的应用．点明下节课深入学习加权平均数内容．
2.7板书设计 七、板书设计8.1.1平均数（一）一.算术平均数的定义 五.课堂练习二.想一想 六.课时小结（求平均数的简便方法）七.作业三.例题讲解 四.议一议（加权平均数） 让学生更好的掌握本节课重要内容及整体框架．
2.8课后作业 八、课后作业习题8.1中的1、2题 独立完成 让学生巩固知识，反馈情况．
3.学情分析：
（1）八年级学生已经初步形成一定的数据收集和处理能力并能根据结果作出合理的决策．同时具有一定的认知发展水平和数学活动经验．
（2）学生在小学对算术平均数的概念和算法已经有了初步的认识，本节课是在小学学习的基础上，对平均数的知识进行巩固、提高和升华．
（3）班级中已经形成小组之间合作交流、勇于探索与实践的良好学风，生生互动、师生互动气氛较浓．
4.教法分析：
为了充分调动学生的积极性，发挥他们的主体性，使他们变被动为主动愉快地学习．在教学过程中，从实际生活中的问题入手，借助多媒体手段，展示精彩片断，提高学习的趣味性和主动性．同时通过类比两种平均数的不同，加深对理性知识的理解．
5.学法分析：
指导学生通过观察、发现、分析、动手操作等过程，充分调动学生学习的积极性和主动性．使他们主动探索，及时发现问题，互相合作，解决问题，形成能力，充分体现教师的主导作用和学生的主体作用．
6.评价分析：
学生是学习的主体，学习是通过学生的主动行为而发生的．在这节课，学生广泛参与，积极主动投入学习活动，学生的主体性得到充分体现．在教学过程中，我始终以学生的个体独立思考为基础，引导学生通过小组内的互相讨论、合作学习，从而构建学生自己的知识体系．同时通过小组内的互相讨论，合作学习，不仅可以提高学，还可以培养学生乐于助人、团结合作的精神，使学生在合作学习中学会学习，学会交往．
PAGE
- 7 -