数学七年级上青岛版3.3有理数的乘方(1)课件
文档属性
| 名称 | 数学七年级上青岛版3.3有理数的乘方(1)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-23 07:45:31 | ||
图片预览










文档简介
课件33张PPT。七第3章 有理数的运算 3.3有理数的乘方(1)
①
②
③ (-2)×(-2)×(-2);
④ (-2)×(-2)×(-2)×(-2)课前热身-116-8教学目标1.通过实例,经历乘方概念的产生过程;
2.理解乘方、幂、指数、底数的概念,掌握乘方与幂的表示法;
3.理解幂的符号法则,会进行有理数的乘方运算;
4.通过对生活中学生感兴趣的问题计算表示,了解乘方运算的必要。教学重点:乘方概念及计算。 教学难点: 乘方、幂、底数、指数等概念以及乘方结果符号的确定。 创设情境,导入新课如图回答下列问题:
(1)怎样计算边长为7厘米的正方形的面积?
(2)怎样计算棱长为5厘米的立方体的体积?
《变式一》如果边长为a厘米的正方形的面积呢?
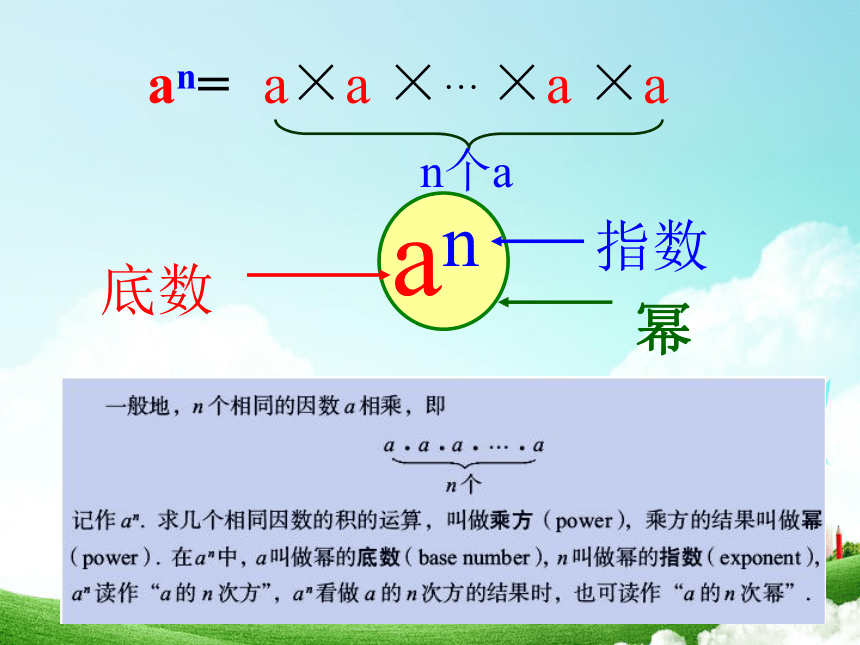
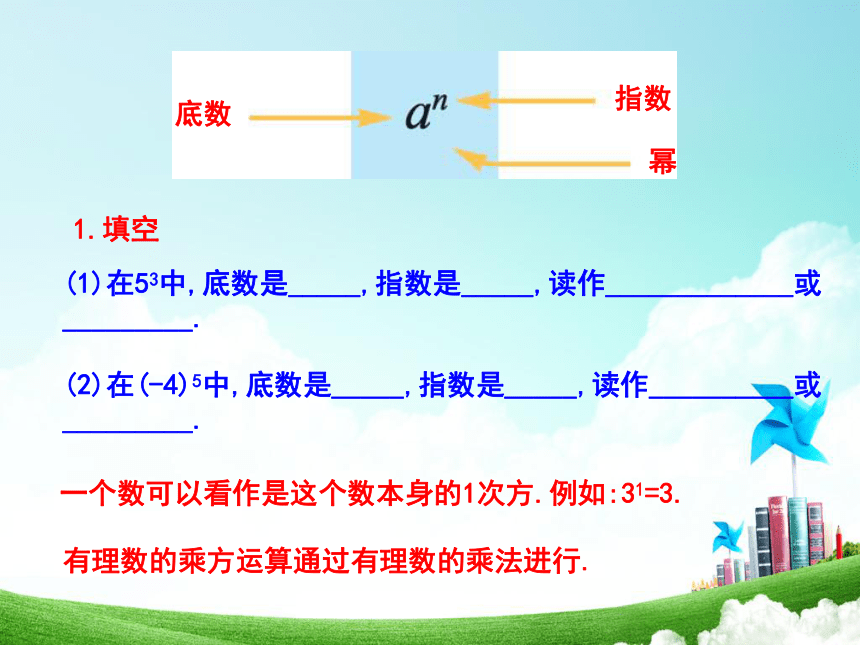
棱长为b厘米的立方体的体积呢? a25×5×5=1257×7=49b3记作25求n个相同因数a的积的运算叫做乘方 有理数的乘方an底数指数幂an=底数指数幂(1)在53中,底数是_____,指数是_____,读作_____________或_________.(2)在(-4)5中,底数是_____,指数是_____,读作__________或_________.1.填空一个数可以看作是这个数本身的1次方.例如:31=3.有理数的乘方运算通过有理数的乘法进行.例 :计算
(1) (-4)3
( 2 )
(3) 23
( 4 ) 42
( 5 ) 03
乘方运算的符号规律正数的任何次幂都是正数
负数的偶次幂是正数,奇次幂是负数
0的正整数次幂都等于0
(-3)4 表示4个-3相乘.
-34表示4个3相乘的相反数.2.说出下列各式的底数、指数、及其意义
(1) 53 (2)(-3)4 ; -34
(3) ; ( 4 )
( 5 ) 5 ; (6) -34读作:34的相反数,而(-3)4读作:-3的四次方;-34=-81, (-3)4=81;底数与指数的区别。(1)-34与(-3)4的区别在哪里?1、判断下列各题是否正确
① 23=2 ×3 ( )
② 2+2+2=23 ( )
23=2×2 ×2 ( )
(-3)(-3)(-3)(-3)= -34( )
不正确不正确正确学以致用不正确(2)(-4)2底数是______指数是______(-4)2=_______(3)34表示___个___ 相乘(4)(-2)3=______-8(5)(+1)2003 -(- 1)2002=___0(6)- 14+1=______03或-3(1)______的平方等于9课堂小结 通过这节课的学习, 你有哪些收获和体会? 1.乘方的意义
2. 正确区分幂的底数和指数,写一个负数或分数的乘方时,底数必须加括号。
3.幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。(任何数的偶次幂都是非负数。)0的正整数次幂都等于0。颗粒归仓一个数可以看作是这个数本身的1次方.有理数的乘方运算通过有理数的乘法进行.颗粒归仓解: (1)-4,4,256. (2) -1,7,-1. 解: (1) (2) 课堂检测3.(1)(-1)12 ,指数是 。
(2)(-3)11表示 个 _相乘。
(3)(-1)2004=____;
(-1)2005=____;
(-1)2n=___(n为正整数);
(-1)2n+1=__(n为正整数)
4.计算: 你真棒!判断
(1) 负数的偶次幂是正数。 ( )
(2) 有理数的偶次幂都是正数。( )
(3) 负数的奇次幂是负数。( )
2、计算:
= =
= √×√-125-0.0011(必做题) 63页 练习3题.
65页 A组1,2题.
(选做题)你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,将两头捏合在一起拉伸,再捏合,再拉伸,重复几次,就把很粗的面条拉成了许多细的面条。问这样捏合到几次后可拉出128根面条呢?
布置作业珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈ 谢谢大家再见第3章 有理数的运算 3.3有理数的乘方(2)
创设情景在日常生活中经常会遇到一些较大的数,如:全世界人口约是6100000000,光的速度大约是300000000米/秒,银河系中的恒星约有160000000000个等等。
怎样来简单的表示这些数呢?交流与发现 根据乘方的意义,填写下表:你发现了什么规律? 例:300 000 000 与 149 000 000 000怎样用10的乘方表示? 用科学记数法表示一个数,你发现有什么规律? 例4 下列用科学计数法表示的数,原来是什么数?
(1)准确数:与实际完全相同的数
近似数:四舍五入得到的与实际相近的数
例5、2010年我国国内生产总值397983亿元请按要求取近似数,用科学计数法表示出来。
(1)精确到十亿(2)精确到百亿
(3)精确到千亿(4)精确到万亿解:(1)10 000
=1×104(2)800 000
=8×105(3)-56 000 000
=-5.6×107(4)-2 030 000 000
=-2.03×109解: (1)10 000 000 (2)-6 000 (3)8 500 000 (4)-39 600解: (1)6.7×103 公顷;5×103 公顷 ;1.5×104 株;1.755×108 株.
(2) 5.1×108 吨.巩固训练1、作业本:63页 练习 3题.
72页 4 题5题.
2、习题3.3 1、2、3、6、7、8、9 做在 课本上
3、基础训练3.3 第一二课时
①
②
③ (-2)×(-2)×(-2);
④ (-2)×(-2)×(-2)×(-2)课前热身-116-8教学目标1.通过实例,经历乘方概念的产生过程;
2.理解乘方、幂、指数、底数的概念,掌握乘方与幂的表示法;
3.理解幂的符号法则,会进行有理数的乘方运算;
4.通过对生活中学生感兴趣的问题计算表示,了解乘方运算的必要。教学重点:乘方概念及计算。 教学难点: 乘方、幂、底数、指数等概念以及乘方结果符号的确定。 创设情境,导入新课如图回答下列问题:
(1)怎样计算边长为7厘米的正方形的面积?
(2)怎样计算棱长为5厘米的立方体的体积?
《变式一》如果边长为a厘米的正方形的面积呢?
棱长为b厘米的立方体的体积呢? a25×5×5=1257×7=49b3记作25求n个相同因数a的积的运算叫做乘方 有理数的乘方an底数指数幂an=底数指数幂(1)在53中,底数是_____,指数是_____,读作_____________或_________.(2)在(-4)5中,底数是_____,指数是_____,读作__________或_________.1.填空一个数可以看作是这个数本身的1次方.例如:31=3.有理数的乘方运算通过有理数的乘法进行.例 :计算
(1) (-4)3
( 2 )
(3) 23
( 4 ) 42
( 5 ) 03
乘方运算的符号规律正数的任何次幂都是正数
负数的偶次幂是正数,奇次幂是负数
0的正整数次幂都等于0
(-3)4 表示4个-3相乘.
-34表示4个3相乘的相反数.2.说出下列各式的底数、指数、及其意义
(1) 53 (2)(-3)4 ; -34
(3) ; ( 4 )
( 5 ) 5 ; (6) -34读作:34的相反数,而(-3)4读作:-3的四次方;-34=-81, (-3)4=81;底数与指数的区别。(1)-34与(-3)4的区别在哪里?1、判断下列各题是否正确
① 23=2 ×3 ( )
② 2+2+2=23 ( )
23=2×2 ×2 ( )
(-3)(-3)(-3)(-3)= -34( )
不正确不正确正确学以致用不正确(2)(-4)2底数是______指数是______(-4)2=_______(3)34表示___个___ 相乘(4)(-2)3=______-8(5)(+1)2003 -(- 1)2002=___0(6)- 14+1=______03或-3(1)______的平方等于9课堂小结 通过这节课的学习, 你有哪些收获和体会? 1.乘方的意义
2. 正确区分幂的底数和指数,写一个负数或分数的乘方时,底数必须加括号。
3.幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。(任何数的偶次幂都是非负数。)0的正整数次幂都等于0。颗粒归仓一个数可以看作是这个数本身的1次方.有理数的乘方运算通过有理数的乘法进行.颗粒归仓解: (1)-4,4,256. (2) -1,7,-1. 解: (1) (2) 课堂检测3.(1)(-1)12 ,指数是 。
(2)(-3)11表示 个 _相乘。
(3)(-1)2004=____;
(-1)2005=____;
(-1)2n=___(n为正整数);
(-1)2n+1=__(n为正整数)
4.计算: 你真棒!判断
(1) 负数的偶次幂是正数。 ( )
(2) 有理数的偶次幂都是正数。( )
(3) 负数的奇次幂是负数。( )
2、计算:
= =
= √×√-125-0.0011(必做题) 63页 练习3题.
65页 A组1,2题.
(选做题)你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,将两头捏合在一起拉伸,再捏合,再拉伸,重复几次,就把很粗的面条拉成了许多细的面条。问这样捏合到几次后可拉出128根面条呢?
布置作业珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?≈ ≈ 谢谢大家再见第3章 有理数的运算 3.3有理数的乘方(2)
创设情景在日常生活中经常会遇到一些较大的数,如:全世界人口约是6100000000,光的速度大约是300000000米/秒,银河系中的恒星约有160000000000个等等。
怎样来简单的表示这些数呢?交流与发现 根据乘方的意义,填写下表:你发现了什么规律? 例:300 000 000 与 149 000 000 000怎样用10的乘方表示? 用科学记数法表示一个数,你发现有什么规律? 例4 下列用科学计数法表示的数,原来是什么数?
(1)准确数:与实际完全相同的数
近似数:四舍五入得到的与实际相近的数
例5、2010年我国国内生产总值397983亿元请按要求取近似数,用科学计数法表示出来。
(1)精确到十亿(2)精确到百亿
(3)精确到千亿(4)精确到万亿解:(1)10 000
=1×104(2)800 000
=8×105(3)-56 000 000
=-5.6×107(4)-2 030 000 000
=-2.03×109解: (1)10 000 000 (2)-6 000 (3)8 500 000 (4)-39 600解: (1)6.7×103 公顷;5×103 公顷 ;1.5×104 株;1.755×108 株.
(2) 5.1×108 吨.巩固训练1、作业本:63页 练习 3题.
72页 4 题5题.
2、习题3.3 1、2、3、6、7、8、9 做在 课本上
3、基础训练3.3 第一二课时
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
