微专题6 概率统计的综合应用-2024年高考一轮复习数学人教A版专题讲义(教案)
文档属性
| 名称 | 微专题6 概率统计的综合应用-2024年高考一轮复习数学人教A版专题讲义(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览




文档简介
微专题6 概率统计的综合应用
概率与统计问题主要考查学生的阅读理解能力和数据分析能力.要从已知数表、题干信息中经过阅读分析判断获取关键信息,搞清各数据、各事件间的关系,建立相应的数学模型.概率与统计问题在近几年的高考中背景取自现实,题型新颖,综合性增强.
【方法储备】
概率和统计综合问题主要包括:①概率与统计中列联表的综合问题;②概率与统计中线性回归方程的综合问题;③概率与统计指标的综合问题;④概率与简单随机抽样的综合问题;⑤概率与统计图的综合问题等几种类型.
【典例精讲】
例1.( 2023·黑龙江省齐齐哈尔市模拟) 羽毛球运动具有拼搏、进步、积极向上的意义,同时还要求运动员具备细心和迅速的敏锐性某大学羽毛球运动协会为了了解本校学生对羽毛球运动是否有兴趣,从该校学生中随机抽取了人进行调查,男女人数之比是:,其中女生对羽毛球运动有兴趣的占,而男生有人表示对羽毛球运动没有兴趣.
完成列联表,根据小概率值的独立性检验,能否认为“对羽毛球运动是否有兴趣与性别有关”?
有兴趣 没兴趣 合计
男
女
合计
为了提高同学们对羽毛球运动的参与度,该校举行一次羽毛球比赛比赛分两个阶段进行,第一阶段的比赛赛制采取单循环方式,每场比赛采取三局二胜制,然后由积分的多少选出进入第二阶段比赛的同学,每场积分规则如下:比赛中以:取胜的同学积分,负的同学积分;以:取胜的同学积分,负的同学积分其中,小强同学和小明同学的比赛倍受关注,设每局小强同学取胜的概率为,记小强同学所得积分为,求的分布列和期望.
附表:,其中.
例2.( 2023·辽宁省鞍山市模拟) 年,是人类首次成功从北坡登顶珠峰周年,也是中国首次精确测定并公布珠峰高程的周年.华为帮助中国移动开通珠峰峰顶,有助于测量信号的实时开通,为珠峰高程测量提供通信保障,也验证了超高海拔地区信号覆盖的可能性,在持续高风速下信号的稳定性,在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说:“华为公司价值体系的理想是为人类服务.”有人曾问,“在珠峰开通的意义在哪里?”我认为它是科学技术的一次珠峰登顶,告诉全世界,华为、中国的底气来自哪里现在的到来给人们的生活带来更加颠覆性的变革,某公司基于领先技术的支持,经济收入在短期内逐月攀升,该公司在月份至月份的经济收入单位:百万元关于月份的数据如下表所示,并根据数据绘制了如下图所示的散点图.
月份
收入百万元
根据散点图判断,与均为正常数哪一个更适宜作为经济收入关于月份的回归方程类型?给出判断即可,不必说明理由
根据的结果及表中的数据,求出关于的回归方程,并预测该公司月份的经济收入.结果保留小数点后两位
从前个月的收入中抽取个,记收入超过百万元的个数为,求的分布列和数学期望.
参考数据:
其中,设,.
参考公式:对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计公式分别为,.
例3.( 2023·广东省湛江市月考) 为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内,,三类行业共个单位的生态环境治理成效进行了考核评估,考评分数达到分及其以上的单位被称为“星级”环保单位,未达到分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的个单位,其考评分数如下:
类行业:,,,,,;
类行业:,,,,,;
类行业:,,,,,,,.
Ⅰ计算该城区这三类行业中每类行业的单位个数;
Ⅱ若从抽取的类行业这个单位中,再随机选取个单位进行某项调查,求选出的这个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
【拓展提升】
练1-1(2023·湖北省黄冈市月考) 某公司为了对一种新产品进行合理定价,将该产品按亊先拟定的价格进行试销,得到如下数据:
单价 元
销量 件
由表中数据求得线性回归方程为若在这些样本点中任取一点,则它在回归直线右上方的概率为( )
A. B. C. D.
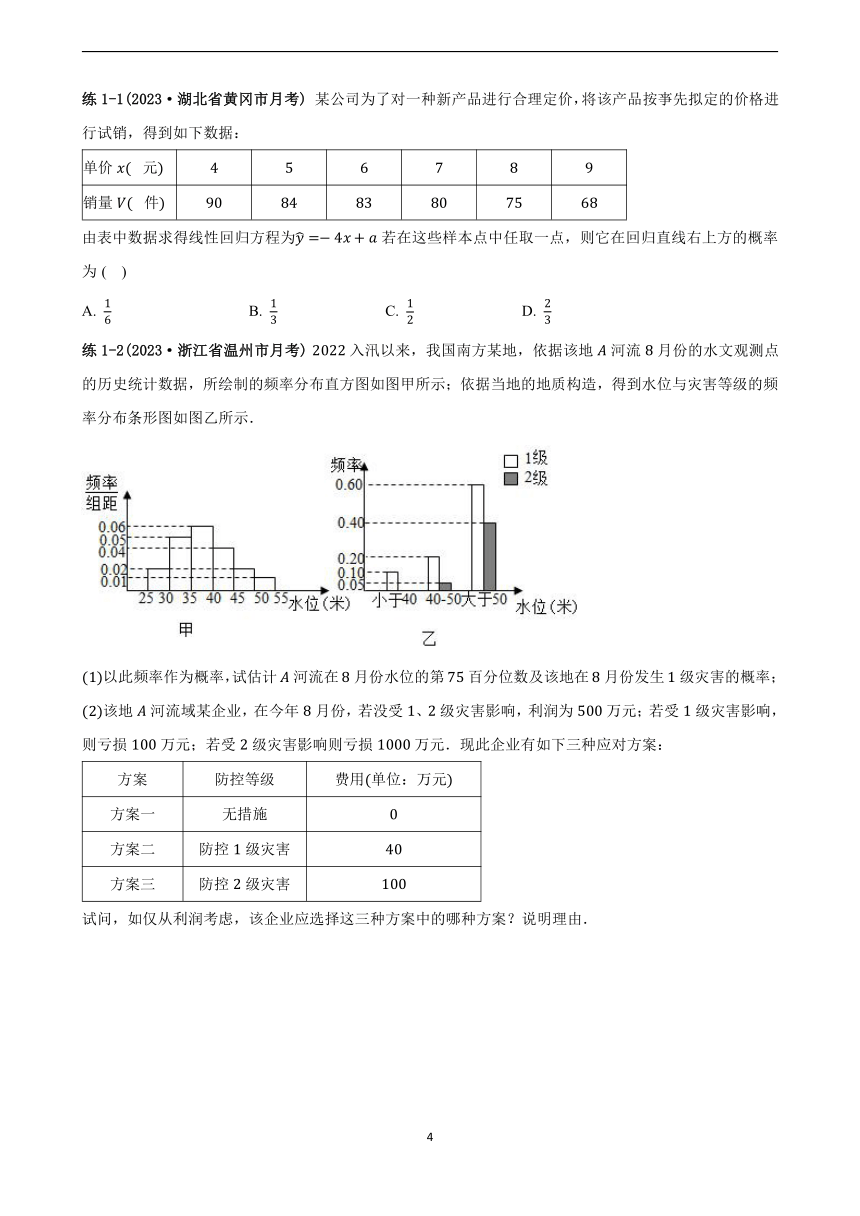
练1-2(2023·浙江省温州市月考) 入汛以来,我国南方某地,依据该地河流月份的水文观测点的历史统计数据,所绘制的频率分布直方图如图甲所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图乙所示.
以此频率作为概率,试估计河流在月份水位的第百分位数及该地在月份发生级灾害的概率;
该地河流域某企业,在今年月份,若没受、级灾害影响,利润为万元;若受级灾害影响,则亏损万元;若受级灾害影响则亏损万元.现此企业有如下三种应对方案:
方案 防控等级 费用单位:万元
方案一 无措施
方案二 防控级灾害
方案三 防控级灾害
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
【方法储备】
概率统计与函数的交汇问题,本质仍是以概率统计为主导,利用函数辅助求解,综合性较强.利用概率统计知识,求解概率、均值、方差等的最值,通常以概率为变量转化为函数问题,建立函数模型,利用单调性求最值.
【典例精讲】
例4.( 2023·安徽省合肥市模拟) 蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出吨该蔬菜获利元,未售出的蔬菜低价处理,每吨亏损元.统计该蔬菜以往个销售周期的市场需求量,绘制右图所示频率分布直方图.
Ⅰ求的值,并求个销售周期的平均市场需求量以各组的区间中点值代表该组的数值:
Ⅱ若经销商在下个销售周期购进了吨该蔬菜,设为该销售周期的利润单位:元,为该销售周期的市场需求量单位:吨求与的函数解析式,并估计销售的利润不少于元的概率.
例5. (2023·陕西省西安市模拟) 近日,河南突降暴雨,郑州、驻马店等多地陷入灾情.习近平总书记对防汛救灾工作作出重要指示,各地迅速向河南伸出援手,体现了“一方有难,八方支援”的人间真情.
降雨重现期是指在一定年代的降雨量记录资料统计期间内,大于或等于某暴雨强度的降雨出现一次的平均间隔时间.现已知近年来郑州市暴雨强度与降雨历时具有的关系大致是.
其中中间变量与降雨重现期年具有如图所示的关系.
现有两个回归模型可供选择:
①根据与成正相关关系,直接采用线性回归模型;
②根据与成正相关关系,且考虑模型拟合曲线的增减速率,采用回归模型.
相关数据统计如下表其中:
,, ,, ,,.
请选择合适的回归模型,求出暴雨强度、降雨历时、降雨重现期年具有的函数关系;
已知郑州月日时时降雨量曾经达到过请利用得到的函数关系,分析“今年河南的暴雨千年一遇”这种说法的合理性.参考数据:,
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为
,.
【拓展提升】
练2-1(2023·安徽省合肥市期末) 某企业为了解年广告费单位:万元对年销售额单位:万元的影响,统计了近年的年广告费和年销售额的数据,得到下面的表格:
年广告费
年销售额
由表中数据,变量,的相关系数,可判定变量,的线性相关关系较强.
建立关于的线性回归方程
已知该企业的年利润与,的关系为根据的结果,年广告费约为何值时小数点后保留一位,年利润的预报值最大
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,.
参考数据:,.
练2-2(2023·广东省广州市模拟) 一企业生产某种产品,通过加大技术创新投入降低了每件产品成本.为了调查年技术创新投入单位:千万元对每件产品成本单位:元的影响,对近年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
根据散点图可知,可用函数模型拟合与的关系,试建立关于的回归方程;
已知该产品的年销售额单位:千万元与每件产品成本的关系为该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据的结果回答:当年技术创新投入为何值时,年利润的预报值最大?注:年利润年销售额年投入成本
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为:,.
【方法储备】
概率统计与导数的综合问题上,解题的难点是建立函数模型,如独立性检验统计量、期望方差公式、正态分布函数和用分布列建立其他的函数的模型,利用导数研究单调性.
【典例精讲】
例6.( 2023·山西省太原市模拟) 某剧场的座位数量是固定的,管理人员统计了最近在该剧场举办的五场表演的票价单位:元和上座率上座人数与总座位数的比值的数据,其中,,,,,并根据统计数据得到如下的散点图:
Ⅰ由散点图判断与哪个模型能更好地对与的关系进行拟合给出判断即可,不必说明理由,并根据你的判断结果求回归方程;
Ⅱ根据Ⅰ所求的回归方程,预测票价为多少时,剧场的门票收入最多.
参考数据:,,,;设,
则,,,,,.
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为:,.
例7.( 2023·辽宁省沈阳市期中) 在年春节期间,为了进一步发挥电子商务在活跃消费市场方面的积极作用,保障人民群众度过一个平安健康快乐祥和的新春佳节,甲公司和乙公司在某购物平台上同时开启了打折促销,直播带年货活动,甲公司和乙公司所售商品类似,存在竞争关系.
现对某时间段名观看直播后选择这两个公司直播间购物的情况进行调查,得到如下数据:
选择甲公司直播间购物 选择乙公司直播间购物 合计
用户年龄段岁
用户年龄段岁
合计
是否有的把握认为选择哪家直播间购物与用户的年龄有关
若小李连续两天每天选择在甲、乙其中一个直播间进行购物,第一天等可能地从甲、乙两家中选一家直播间购物,如果第一天去甲直播间购物,那么第二天去甲直播间购物的概率为如果第一天去乙直播间购物,那么第二天去甲直播间购物的概率为,求小李第二天去乙直播间购物的概率
元旦期间,甲公司购物平台直播间进行“秒杀”活动,假设直播间每人下单成功的概率均为,每人下单成功与否互不影响,若从直播间中随机抽取五人,记五人中恰有人下单成功的概率为,求的最大值点.
参考公式:,其中.
独立性检验中几个常用的小概率值和相应的临界值表:
【拓展提升】
练3-1(2023·福建省泉州市月考) 港珠澳大桥海底隧道是当今世界上埋深最大、综合技术难度最高的沉管隧道,建设过程中突破了许多世界级难题,其建成标志着我国在隧道建设领域已达到世界领先水平.在开挖隧道施工过程中,若隧道拱顶下沉速率过快,无法保证工程施工的安全性,则需及时调整支护参数.某施工队对正在施工的隧道工程进行下沉量监控量测工作,通过对监控量测结果进行回归分析,建立前天隧道拱顶的累加总下沉量单位:毫米与时间单位:天的回归方程,通过回归方程预测是否需要调整支护参数.已知该隧道拱顶下沉的实测数据如下表所示:
研究人员制作相应散点图,通过观察,拟用函数进行拟合.令,计算得:,,,,,
.
请判断是否可以用线性回归模型拟合与的关系;通常时,认为可以用线性回归模型拟合变量间的关系
试建立与的回归方程,并预测前天该隧道拱顶的累加总下沉量;
已知当拱顶下沉速率超过毫米天,支护系统将超负荷,隧道有塌方风险.若规定每天下午点为调整支护参数的时间,试估计最迟在第几天需调整支护参数,才能避免塌方.
附:①相关系数;
②回归直线中斜率和截距的最小二乘估计公式分别为:,.
③参考数据:,.
练3-2(2023·浙江省杭州市联考) 某种产品以往各年的宣传费用支出万元与销售量万件之间有如下对应数据:
试求回归直线方程;
设该产品的单件售价与单件生产成本的差为元,若与销售量万件的函数关系是,试估计宣传费用支出为多少万元时,销售该产品的利润最大?注:销售利润销售额生产成本宣传费用
参考数据与公式:,,
【方法储备】
概率统计问题与数列的交汇问题,要准确把题中所涉及的事件进行分解,明确所求问题所属的事件类型是关键.解答此类问题,一是要根据题意建立数列模型;二是熟练的利用已知的求概率的方法进行概率计算.概率与数列的交汇问题的常见类型有:
①求通项公式:关键是找出概率或数学期望的递推关系式,根据数列部分由递推公式求通项公式的方法,求出概率或期望的通项公式;
②利用等差、等比数列的性质,研究单调性、最值或求极限;
③求和:利用数列中的倒序求和、错位求和、裂项求和等方法.
【典例精讲】
例8.( 2023·江苏省南通市联考) 随着时代发展和社会进步,教师职业越来越受青睐,考取教师资格证成为不少人的就业规划之一.当前,中小学教师资格考试分笔试和面试两部分.已知某市年共有名考生参加了中小学教师资格考试的笔试,现从中随机抽取人的笔试成绩满分视为分,得到如下数据:
不及格 及格
师范类毕业
非师范类毕业
Ⅰ能否有的把握认为考生的笔试成绩与是否为师范类毕业有关?
Ⅱ考生甲为提升笔试成绩,报名参加了某教师资格考试知识竞赛,该竞赛要回答,两类问题,每位参赛者回答次,每次回答一个问题,若回答正确,则下一个问题从类中随机抽取;若回答错误,则下一个问题从类中随机抽取.规定每位参赛者回答的第一个问题从类中抽取,已知考生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且每次回答问题正确与否是相互独立的,求考生甲第次回答正确的概率.
附:,其中.
【拓展提升】
练4-1(2023·重庆市市辖区模拟) 中围男篮历史上曾次参加亚运会,其中次夺得金牌,是亚运会夺冠次数最多的球队第届亚运会将于年月日至月日在杭州举办.
为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各名进行调查,得到列联表如下:
喜爱篮球 不喜爱 合计
男生
女生
合计
依据小概率值的独立性检验,能否认为喜爱篮球运动与性别有关
校篮球队中的甲、乙、丙三名球员将进行传球训练,第次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到记开始传球的人为第次触球者,第次触球者是甲的概率记为,即.
求,,并证明:为等比数列:
比较第次触球者是甲与第次触球者是乙的概率的大小.
参考公式:,其中为样本容量.
练4-2(2023·四川省成都市模拟) 某火锅店年月份生意日渐火爆,年月日至日该店的日销售量份如下表:
日期
日销售量份
由散点图可知,日销售量与日期之间有较好的线性相关关系,请根据该关系预计到年月几日该火锅店的日销售量可以超过份
该火锅店为了回馈和吸引更多的顾客,决定在年月日对来店吃火锅的每位顾客在结算时进行优惠,优惠政策为:如果选择的是辣锅底,则每位顾客优惠元,如果选择的是不辣锅底,则每位顾客优惠元,已知每位顾客选择辣锅底的概率均为,且顾客之间的选择是相互独立的.
从当天的顾客中随机抽取人,记优惠的总钱数为,求的分布列与数学期望;
(ⅱ)若对已经优惠的钱数进行累计,求累计钱数为元的概率.
参考公式:回归直线,
其中,.
【答案解析】
例1.解:
有兴趣 没兴趣 合计
男
女
合计
零假设 对羽毛球运动感兴趣与性别无关.
,
故根据小概率值 的独立性检验,假设成立,我们认为“对羽毛球运动是否有兴趣与性别无关”.
由题意可知随机变量的取值为,,,,
; ;
; ;
故的分布列为:
.
例2.解:根据散点图判断, 更适宜作为经济收入关于月份的回归方程类型;
因为 ,所以两边同时取常用对数,得 ,
设 ,所以 ,
因为 ,所以
所以 .
所以 ,即 ,所以 .
令 ,得: ,
故预测该公司月份的经济收入大约为百万元.
前个月的收入中,收入超过百万元的有个,所以的取值为,,,
所以的分布列为:
所以 .
例3.解:Ⅰ由题意,抽取的三类行业单位个数之比为.
由分层抽样的定义,有类行业单位个数为个;
类行业单位个数为个;
类行业单位个数为个.
,,三类行业单位的个数分别为,,.
Ⅱ记选出的这个单位中既有“星级”环保单位,又有“非星级”环保单位为事件.
在类行业的个单位中随机选取个单位的考核数据情形有:
,,,,,,,,,,,,,,,,,,,共种.
选出的这个单位都是“星级”环保单位的考核数据情形有:,,,共种.
这个单位都是“非星级”环保单位的考核数据情形有种.
这个单位都是“星级”环保单位或都是“非星级”环保单位的情形共种.
所求概率.
练1-1.解:,
,
过样本中心点,,
回归直线方程;
数据,,,,,.
个点中有个点在直线右上方,即,,.
从这些样本点中任取点,共有种不同的取法,
故这点恰好在回归直线右上方的概率为.
故选:.
练1-2.解:频率分布直方图中个小矩形的面积分别是,,,,,,
设月份的水位第百分位数为,则,
,
则,
月份的第百分位数为;
设该河流月份水位小于米为事件,水位在米至米为事件,水位大于米为事件,
,,,
设该地发生级灾害为事件,
由条形图可知:,,,
,,
,
;
由可知月份该河流不发生灾害的概率为
,
发生级灾害的概率为,发生级灾害的概率为,
设第种方案的企业利润为,
若选择方案一,则该企业在月份的平均利润
万元,
若选择方案二,则该企业在月份的平均利润
万元,
若选择方案三,则该企业在月份的平均利润
万元,
由于,
故企业应选择方案二.
例4.解:Ⅰ,解得,
个销售周期的平均市场需求量为:
.
Ⅱ由题意得,当,,
当时,
所以与的函数解析式为
设销售利润不少于元的时间记为.
当,,
当,,
所以,所以.
例5. 解:由图中散点图的走势,选择回归模型,
利用最小二乘法可得,
,
,
因此中间变量与降雨重现期的线性回归方程为,
结合题意可得,暴雨强度、降雨历时、降雨重现期年具有的函数关系是;
由题意可得,,并代入到中函数关系,可得
,解得年.
故可以认为“今年河南的暴雨千年一遇“.
练2-1.解:由表格数据,得,,
由公式得,
,
故关于的线性回归方程为.
由得,
设,所以,
所以,
故当时,取最大值,
所以万元时,年利润的预报值最大.
练2-2.解:令,则关于的线性回归方程为,
依题意,得,
,
则,
所以关于的回归方程为;
由,得,
设年利润为,
则,
当时,年利润取得最大值,此时,
所以当年技术创新投入为千万元时,年利润的预报值最大.
例6.解:Ⅰ 能更好地对与的关系进行拟合.
设 ,先求关于的线性回归方程
由已知得 ,
所以 ,
,
所以关于的线性回归方程为 ,
所以关于的回归方程为 .
Ⅱ设该剧场的总座位数为,由题意得门票收入为 .
设函数 ,则 ,
当 ,即 时,函数单调递减,
当 ,即 时,函数单调递增,
所以 在 处取最大值,
所以预测票价为元时,剧场的门票收入最多.
例7.解:
选择甲公司购物平台 选择乙公司购物平台 合计
用户年龄段岁
用户年龄段
合计
根据列联表可得,
又,,
所以有的把握认为选择哪家直播间购物与用户的年龄有关;
设“第一天去甲直播间购物”,“第一天去乙直播间购物”,“第二天去乙直播间购物”,
根据题意得,,,
则
由题意可知,
当时,,单调递增:
当时,,单调递减:
所以当时,有最大值,故.
练3-1.解:计算,得,,
结合题目数据代入公式,
可得,
因为,所以可以用线性回归模型拟合与的关系.
由,对等式两边取自然对数,得,
令,则,
结合题目数据代入公式,可得,
由,将样本中心点代入,
得,即,
即隧道拱顶累加总下沉量关于时间的回归方程为
令,计算得,
即预测前天该隧道拱顶的累加总下沉量为毫米.
到天时,拱顶累加总下沉量为,
对求导,得拱顶下沉速率,
依题意,当拱顶下沉速率超过毫米天时,,即,
所以,
由参考数据得,,即,
解得,
可知在第天时拱顶下沉速率就已经超过了毫米天
即最晚在第天时,需调整支护参数,才能避免塌方.
练3-2.解:依题意:,,
设回归直线方程为:,
,,
回归直线方程为
由题意得,销售利润万元,
即,
,
时,,
且时,;时,,
当时,最大,
当时,,
估计宣传费用为万元时,销售该产品的利润最大.
例8.解:Ⅰ补充列联表为
不及格 及格 合计
师范类毕业
非师范类毕业
合计
,
所以没有的把握认为考生的笔试成绩与是否为师范类毕业有关.
Ⅱ考生甲第次回答正确的概率只与第次回答是否正确有关,
则,
即,
所以,
又,
所以数列是以为首项,为公比的等比数列,
即,得,
所以考生甲第次回答正确的概率
练4-1.解:假设喜爱篮球运动与性别独立,即喜爱篮球运动与性别无关,
,
根据小概率值的独立性检验,我们推断不成立,
即认为喜爱篮球运动与性别有关,此推断犯错误的概率不超过.
由题意,,
第次触球者是甲的概率记为,则当时,第次触球者是甲的概率为,
第次触球者不是甲的概率为,
则,
从而,又,
是以为首项,公比为的等比数列,
故.
设第次触球者是乙的概率记为,
当时,,
,,
,所以第次触球者是甲的概率大.
练4-2.解:,,
,
,故,
,所以关于的线性回归方程为,
令,考虑实际问题取正整数,解得,
所以预计到年月日该火锅店的日销售量可以超过份.
的可能取值为,,,,,
,,
,,
,所以的分布列为
数学期望元.
由题意可知:已经优惠的钱数累计为元的概率为,
累计不到元的情况只有累计优惠了元,再优惠元,
概率为,而,,即,
,,,
数列是首项为,公比为的等比数列,
,,
累计钱数为元的概率为.
2
概率与统计问题主要考查学生的阅读理解能力和数据分析能力.要从已知数表、题干信息中经过阅读分析判断获取关键信息,搞清各数据、各事件间的关系,建立相应的数学模型.概率与统计问题在近几年的高考中背景取自现实,题型新颖,综合性增强.
【方法储备】
概率和统计综合问题主要包括:①概率与统计中列联表的综合问题;②概率与统计中线性回归方程的综合问题;③概率与统计指标的综合问题;④概率与简单随机抽样的综合问题;⑤概率与统计图的综合问题等几种类型.
【典例精讲】
例1.( 2023·黑龙江省齐齐哈尔市模拟) 羽毛球运动具有拼搏、进步、积极向上的意义,同时还要求运动员具备细心和迅速的敏锐性某大学羽毛球运动协会为了了解本校学生对羽毛球运动是否有兴趣,从该校学生中随机抽取了人进行调查,男女人数之比是:,其中女生对羽毛球运动有兴趣的占,而男生有人表示对羽毛球运动没有兴趣.
完成列联表,根据小概率值的独立性检验,能否认为“对羽毛球运动是否有兴趣与性别有关”?
有兴趣 没兴趣 合计
男
女
合计
为了提高同学们对羽毛球运动的参与度,该校举行一次羽毛球比赛比赛分两个阶段进行,第一阶段的比赛赛制采取单循环方式,每场比赛采取三局二胜制,然后由积分的多少选出进入第二阶段比赛的同学,每场积分规则如下:比赛中以:取胜的同学积分,负的同学积分;以:取胜的同学积分,负的同学积分其中,小强同学和小明同学的比赛倍受关注,设每局小强同学取胜的概率为,记小强同学所得积分为,求的分布列和期望.
附表:,其中.
例2.( 2023·辽宁省鞍山市模拟) 年,是人类首次成功从北坡登顶珠峰周年,也是中国首次精确测定并公布珠峰高程的周年.华为帮助中国移动开通珠峰峰顶,有助于测量信号的实时开通,为珠峰高程测量提供通信保障,也验证了超高海拔地区信号覆盖的可能性,在持续高风速下信号的稳定性,在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说:“华为公司价值体系的理想是为人类服务.”有人曾问,“在珠峰开通的意义在哪里?”我认为它是科学技术的一次珠峰登顶,告诉全世界,华为、中国的底气来自哪里现在的到来给人们的生活带来更加颠覆性的变革,某公司基于领先技术的支持,经济收入在短期内逐月攀升,该公司在月份至月份的经济收入单位:百万元关于月份的数据如下表所示,并根据数据绘制了如下图所示的散点图.
月份
收入百万元
根据散点图判断,与均为正常数哪一个更适宜作为经济收入关于月份的回归方程类型?给出判断即可,不必说明理由
根据的结果及表中的数据,求出关于的回归方程,并预测该公司月份的经济收入.结果保留小数点后两位
从前个月的收入中抽取个,记收入超过百万元的个数为,求的分布列和数学期望.
参考数据:
其中,设,.
参考公式:对于一组具有线性相关关系的数据,其回归直线的斜率和截距的最小二乘估计公式分别为,.
例3.( 2023·广东省湛江市月考) 为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内,,三类行业共个单位的生态环境治理成效进行了考核评估,考评分数达到分及其以上的单位被称为“星级”环保单位,未达到分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的个单位,其考评分数如下:
类行业:,,,,,;
类行业:,,,,,;
类行业:,,,,,,,.
Ⅰ计算该城区这三类行业中每类行业的单位个数;
Ⅱ若从抽取的类行业这个单位中,再随机选取个单位进行某项调查,求选出的这个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
【拓展提升】
练1-1(2023·湖北省黄冈市月考) 某公司为了对一种新产品进行合理定价,将该产品按亊先拟定的价格进行试销,得到如下数据:
单价 元
销量 件
由表中数据求得线性回归方程为若在这些样本点中任取一点,则它在回归直线右上方的概率为( )
A. B. C. D.
练1-2(2023·浙江省温州市月考) 入汛以来,我国南方某地,依据该地河流月份的水文观测点的历史统计数据,所绘制的频率分布直方图如图甲所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图乙所示.
以此频率作为概率,试估计河流在月份水位的第百分位数及该地在月份发生级灾害的概率;
该地河流域某企业,在今年月份,若没受、级灾害影响,利润为万元;若受级灾害影响,则亏损万元;若受级灾害影响则亏损万元.现此企业有如下三种应对方案:
方案 防控等级 费用单位:万元
方案一 无措施
方案二 防控级灾害
方案三 防控级灾害
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
【方法储备】
概率统计与函数的交汇问题,本质仍是以概率统计为主导,利用函数辅助求解,综合性较强.利用概率统计知识,求解概率、均值、方差等的最值,通常以概率为变量转化为函数问题,建立函数模型,利用单调性求最值.
【典例精讲】
例4.( 2023·安徽省合肥市模拟) 蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出吨该蔬菜获利元,未售出的蔬菜低价处理,每吨亏损元.统计该蔬菜以往个销售周期的市场需求量,绘制右图所示频率分布直方图.
Ⅰ求的值,并求个销售周期的平均市场需求量以各组的区间中点值代表该组的数值:
Ⅱ若经销商在下个销售周期购进了吨该蔬菜,设为该销售周期的利润单位:元,为该销售周期的市场需求量单位:吨求与的函数解析式,并估计销售的利润不少于元的概率.
例5. (2023·陕西省西安市模拟) 近日,河南突降暴雨,郑州、驻马店等多地陷入灾情.习近平总书记对防汛救灾工作作出重要指示,各地迅速向河南伸出援手,体现了“一方有难,八方支援”的人间真情.
降雨重现期是指在一定年代的降雨量记录资料统计期间内,大于或等于某暴雨强度的降雨出现一次的平均间隔时间.现已知近年来郑州市暴雨强度与降雨历时具有的关系大致是.
其中中间变量与降雨重现期年具有如图所示的关系.
现有两个回归模型可供选择:
①根据与成正相关关系,直接采用线性回归模型;
②根据与成正相关关系,且考虑模型拟合曲线的增减速率,采用回归模型.
相关数据统计如下表其中:
,, ,, ,,.
请选择合适的回归模型,求出暴雨强度、降雨历时、降雨重现期年具有的函数关系;
已知郑州月日时时降雨量曾经达到过请利用得到的函数关系,分析“今年河南的暴雨千年一遇”这种说法的合理性.参考数据:,
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为
,.
【拓展提升】
练2-1(2023·安徽省合肥市期末) 某企业为了解年广告费单位:万元对年销售额单位:万元的影响,统计了近年的年广告费和年销售额的数据,得到下面的表格:
年广告费
年销售额
由表中数据,变量,的相关系数,可判定变量,的线性相关关系较强.
建立关于的线性回归方程
已知该企业的年利润与,的关系为根据的结果,年广告费约为何值时小数点后保留一位,年利润的预报值最大
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,.
参考数据:,.
练2-2(2023·广东省广州市模拟) 一企业生产某种产品,通过加大技术创新投入降低了每件产品成本.为了调查年技术创新投入单位:千万元对每件产品成本单位:元的影响,对近年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得:,,,,.
根据散点图可知,可用函数模型拟合与的关系,试建立关于的回归方程;
已知该产品的年销售额单位:千万元与每件产品成本的关系为该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据的结果回答:当年技术创新投入为何值时,年利润的预报值最大?注:年利润年销售额年投入成本
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为:,.
【方法储备】
概率统计与导数的综合问题上,解题的难点是建立函数模型,如独立性检验统计量、期望方差公式、正态分布函数和用分布列建立其他的函数的模型,利用导数研究单调性.
【典例精讲】
例6.( 2023·山西省太原市模拟) 某剧场的座位数量是固定的,管理人员统计了最近在该剧场举办的五场表演的票价单位:元和上座率上座人数与总座位数的比值的数据,其中,,,,,并根据统计数据得到如下的散点图:
Ⅰ由散点图判断与哪个模型能更好地对与的关系进行拟合给出判断即可,不必说明理由,并根据你的判断结果求回归方程;
Ⅱ根据Ⅰ所求的回归方程,预测票价为多少时,剧场的门票收入最多.
参考数据:,,,;设,
则,,,,,.
参考公式:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为:,.
例7.( 2023·辽宁省沈阳市期中) 在年春节期间,为了进一步发挥电子商务在活跃消费市场方面的积极作用,保障人民群众度过一个平安健康快乐祥和的新春佳节,甲公司和乙公司在某购物平台上同时开启了打折促销,直播带年货活动,甲公司和乙公司所售商品类似,存在竞争关系.
现对某时间段名观看直播后选择这两个公司直播间购物的情况进行调查,得到如下数据:
选择甲公司直播间购物 选择乙公司直播间购物 合计
用户年龄段岁
用户年龄段岁
合计
是否有的把握认为选择哪家直播间购物与用户的年龄有关
若小李连续两天每天选择在甲、乙其中一个直播间进行购物,第一天等可能地从甲、乙两家中选一家直播间购物,如果第一天去甲直播间购物,那么第二天去甲直播间购物的概率为如果第一天去乙直播间购物,那么第二天去甲直播间购物的概率为,求小李第二天去乙直播间购物的概率
元旦期间,甲公司购物平台直播间进行“秒杀”活动,假设直播间每人下单成功的概率均为,每人下单成功与否互不影响,若从直播间中随机抽取五人,记五人中恰有人下单成功的概率为,求的最大值点.
参考公式:,其中.
独立性检验中几个常用的小概率值和相应的临界值表:
【拓展提升】
练3-1(2023·福建省泉州市月考) 港珠澳大桥海底隧道是当今世界上埋深最大、综合技术难度最高的沉管隧道,建设过程中突破了许多世界级难题,其建成标志着我国在隧道建设领域已达到世界领先水平.在开挖隧道施工过程中,若隧道拱顶下沉速率过快,无法保证工程施工的安全性,则需及时调整支护参数.某施工队对正在施工的隧道工程进行下沉量监控量测工作,通过对监控量测结果进行回归分析,建立前天隧道拱顶的累加总下沉量单位:毫米与时间单位:天的回归方程,通过回归方程预测是否需要调整支护参数.已知该隧道拱顶下沉的实测数据如下表所示:
研究人员制作相应散点图,通过观察,拟用函数进行拟合.令,计算得:,,,,,
.
请判断是否可以用线性回归模型拟合与的关系;通常时,认为可以用线性回归模型拟合变量间的关系
试建立与的回归方程,并预测前天该隧道拱顶的累加总下沉量;
已知当拱顶下沉速率超过毫米天,支护系统将超负荷,隧道有塌方风险.若规定每天下午点为调整支护参数的时间,试估计最迟在第几天需调整支护参数,才能避免塌方.
附:①相关系数;
②回归直线中斜率和截距的最小二乘估计公式分别为:,.
③参考数据:,.
练3-2(2023·浙江省杭州市联考) 某种产品以往各年的宣传费用支出万元与销售量万件之间有如下对应数据:
试求回归直线方程;
设该产品的单件售价与单件生产成本的差为元,若与销售量万件的函数关系是,试估计宣传费用支出为多少万元时,销售该产品的利润最大?注:销售利润销售额生产成本宣传费用
参考数据与公式:,,
【方法储备】
概率统计问题与数列的交汇问题,要准确把题中所涉及的事件进行分解,明确所求问题所属的事件类型是关键.解答此类问题,一是要根据题意建立数列模型;二是熟练的利用已知的求概率的方法进行概率计算.概率与数列的交汇问题的常见类型有:
①求通项公式:关键是找出概率或数学期望的递推关系式,根据数列部分由递推公式求通项公式的方法,求出概率或期望的通项公式;
②利用等差、等比数列的性质,研究单调性、最值或求极限;
③求和:利用数列中的倒序求和、错位求和、裂项求和等方法.
【典例精讲】
例8.( 2023·江苏省南通市联考) 随着时代发展和社会进步,教师职业越来越受青睐,考取教师资格证成为不少人的就业规划之一.当前,中小学教师资格考试分笔试和面试两部分.已知某市年共有名考生参加了中小学教师资格考试的笔试,现从中随机抽取人的笔试成绩满分视为分,得到如下数据:
不及格 及格
师范类毕业
非师范类毕业
Ⅰ能否有的把握认为考生的笔试成绩与是否为师范类毕业有关?
Ⅱ考生甲为提升笔试成绩,报名参加了某教师资格考试知识竞赛,该竞赛要回答,两类问题,每位参赛者回答次,每次回答一个问题,若回答正确,则下一个问题从类中随机抽取;若回答错误,则下一个问题从类中随机抽取.规定每位参赛者回答的第一个问题从类中抽取,已知考生甲能正确回答类问题的概率为,能正确回答类问题的概率为,且每次回答问题正确与否是相互独立的,求考生甲第次回答正确的概率.
附:,其中.
【拓展提升】
练4-1(2023·重庆市市辖区模拟) 中围男篮历史上曾次参加亚运会,其中次夺得金牌,是亚运会夺冠次数最多的球队第届亚运会将于年月日至月日在杭州举办.
为了解喜爱篮球运动是否与性别有关,某学校随机抽取了男生和女生各名进行调查,得到列联表如下:
喜爱篮球 不喜爱 合计
男生
女生
合计
依据小概率值的独立性检验,能否认为喜爱篮球运动与性别有关
校篮球队中的甲、乙、丙三名球员将进行传球训练,第次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到记开始传球的人为第次触球者,第次触球者是甲的概率记为,即.
求,,并证明:为等比数列:
比较第次触球者是甲与第次触球者是乙的概率的大小.
参考公式:,其中为样本容量.
练4-2(2023·四川省成都市模拟) 某火锅店年月份生意日渐火爆,年月日至日该店的日销售量份如下表:
日期
日销售量份
由散点图可知,日销售量与日期之间有较好的线性相关关系,请根据该关系预计到年月几日该火锅店的日销售量可以超过份
该火锅店为了回馈和吸引更多的顾客,决定在年月日对来店吃火锅的每位顾客在结算时进行优惠,优惠政策为:如果选择的是辣锅底,则每位顾客优惠元,如果选择的是不辣锅底,则每位顾客优惠元,已知每位顾客选择辣锅底的概率均为,且顾客之间的选择是相互独立的.
从当天的顾客中随机抽取人,记优惠的总钱数为,求的分布列与数学期望;
(ⅱ)若对已经优惠的钱数进行累计,求累计钱数为元的概率.
参考公式:回归直线,
其中,.
【答案解析】
例1.解:
有兴趣 没兴趣 合计
男
女
合计
零假设 对羽毛球运动感兴趣与性别无关.
,
故根据小概率值 的独立性检验,假设成立,我们认为“对羽毛球运动是否有兴趣与性别无关”.
由题意可知随机变量的取值为,,,,
; ;
; ;
故的分布列为:
.
例2.解:根据散点图判断, 更适宜作为经济收入关于月份的回归方程类型;
因为 ,所以两边同时取常用对数,得 ,
设 ,所以 ,
因为 ,所以
所以 .
所以 ,即 ,所以 .
令 ,得: ,
故预测该公司月份的经济收入大约为百万元.
前个月的收入中,收入超过百万元的有个,所以的取值为,,,
所以的分布列为:
所以 .
例3.解:Ⅰ由题意,抽取的三类行业单位个数之比为.
由分层抽样的定义,有类行业单位个数为个;
类行业单位个数为个;
类行业单位个数为个.
,,三类行业单位的个数分别为,,.
Ⅱ记选出的这个单位中既有“星级”环保单位,又有“非星级”环保单位为事件.
在类行业的个单位中随机选取个单位的考核数据情形有:
,,,,,,,,,,,,,,,,,,,共种.
选出的这个单位都是“星级”环保单位的考核数据情形有:,,,共种.
这个单位都是“非星级”环保单位的考核数据情形有种.
这个单位都是“星级”环保单位或都是“非星级”环保单位的情形共种.
所求概率.
练1-1.解:,
,
过样本中心点,,
回归直线方程;
数据,,,,,.
个点中有个点在直线右上方,即,,.
从这些样本点中任取点,共有种不同的取法,
故这点恰好在回归直线右上方的概率为.
故选:.
练1-2.解:频率分布直方图中个小矩形的面积分别是,,,,,,
设月份的水位第百分位数为,则,
,
则,
月份的第百分位数为;
设该河流月份水位小于米为事件,水位在米至米为事件,水位大于米为事件,
,,,
设该地发生级灾害为事件,
由条形图可知:,,,
,,
,
;
由可知月份该河流不发生灾害的概率为
,
发生级灾害的概率为,发生级灾害的概率为,
设第种方案的企业利润为,
若选择方案一,则该企业在月份的平均利润
万元,
若选择方案二,则该企业在月份的平均利润
万元,
若选择方案三,则该企业在月份的平均利润
万元,
由于,
故企业应选择方案二.
例4.解:Ⅰ,解得,
个销售周期的平均市场需求量为:
.
Ⅱ由题意得,当,,
当时,
所以与的函数解析式为
设销售利润不少于元的时间记为.
当,,
当,,
所以,所以.
例5. 解:由图中散点图的走势,选择回归模型,
利用最小二乘法可得,
,
,
因此中间变量与降雨重现期的线性回归方程为,
结合题意可得,暴雨强度、降雨历时、降雨重现期年具有的函数关系是;
由题意可得,,并代入到中函数关系,可得
,解得年.
故可以认为“今年河南的暴雨千年一遇“.
练2-1.解:由表格数据,得,,
由公式得,
,
故关于的线性回归方程为.
由得,
设,所以,
所以,
故当时,取最大值,
所以万元时,年利润的预报值最大.
练2-2.解:令,则关于的线性回归方程为,
依题意,得,
,
则,
所以关于的回归方程为;
由,得,
设年利润为,
则,
当时,年利润取得最大值,此时,
所以当年技术创新投入为千万元时,年利润的预报值最大.
例6.解:Ⅰ 能更好地对与的关系进行拟合.
设 ,先求关于的线性回归方程
由已知得 ,
所以 ,
,
所以关于的线性回归方程为 ,
所以关于的回归方程为 .
Ⅱ设该剧场的总座位数为,由题意得门票收入为 .
设函数 ,则 ,
当 ,即 时,函数单调递减,
当 ,即 时,函数单调递增,
所以 在 处取最大值,
所以预测票价为元时,剧场的门票收入最多.
例7.解:
选择甲公司购物平台 选择乙公司购物平台 合计
用户年龄段岁
用户年龄段
合计
根据列联表可得,
又,,
所以有的把握认为选择哪家直播间购物与用户的年龄有关;
设“第一天去甲直播间购物”,“第一天去乙直播间购物”,“第二天去乙直播间购物”,
根据题意得,,,
则
由题意可知,
当时,,单调递增:
当时,,单调递减:
所以当时,有最大值,故.
练3-1.解:计算,得,,
结合题目数据代入公式,
可得,
因为,所以可以用线性回归模型拟合与的关系.
由,对等式两边取自然对数,得,
令,则,
结合题目数据代入公式,可得,
由,将样本中心点代入,
得,即,
即隧道拱顶累加总下沉量关于时间的回归方程为
令,计算得,
即预测前天该隧道拱顶的累加总下沉量为毫米.
到天时,拱顶累加总下沉量为,
对求导,得拱顶下沉速率,
依题意,当拱顶下沉速率超过毫米天时,,即,
所以,
由参考数据得,,即,
解得,
可知在第天时拱顶下沉速率就已经超过了毫米天
即最晚在第天时,需调整支护参数,才能避免塌方.
练3-2.解:依题意:,,
设回归直线方程为:,
,,
回归直线方程为
由题意得,销售利润万元,
即,
,
时,,
且时,;时,,
当时,最大,
当时,,
估计宣传费用为万元时,销售该产品的利润最大.
例8.解:Ⅰ补充列联表为
不及格 及格 合计
师范类毕业
非师范类毕业
合计
,
所以没有的把握认为考生的笔试成绩与是否为师范类毕业有关.
Ⅱ考生甲第次回答正确的概率只与第次回答是否正确有关,
则,
即,
所以,
又,
所以数列是以为首项,为公比的等比数列,
即,得,
所以考生甲第次回答正确的概率
练4-1.解:假设喜爱篮球运动与性别独立,即喜爱篮球运动与性别无关,
,
根据小概率值的独立性检验,我们推断不成立,
即认为喜爱篮球运动与性别有关,此推断犯错误的概率不超过.
由题意,,
第次触球者是甲的概率记为,则当时,第次触球者是甲的概率为,
第次触球者不是甲的概率为,
则,
从而,又,
是以为首项,公比为的等比数列,
故.
设第次触球者是乙的概率记为,
当时,,
,,
,所以第次触球者是甲的概率大.
练4-2.解:,,
,
,故,
,所以关于的线性回归方程为,
令,考虑实际问题取正整数,解得,
所以预计到年月日该火锅店的日销售量可以超过份.
的可能取值为,,,,,
,,
,,
,所以的分布列为
数学期望元.
由题意可知:已经优惠的钱数累计为元的概率为,
累计不到元的情况只有累计优惠了元,再优惠元,
概率为,而,,即,
,,,
数列是首项为,公比为的等比数列,
,,
累计钱数为元的概率为.
2
同课章节目录
