江苏省苏州工业园区星海实验初级中学2023-2024学年第一学期初二数学期中考试试卷(图片版,无答案)
文档属性
| 名称 | 江苏省苏州工业园区星海实验初级中学2023-2024学年第一学期初二数学期中考试试卷(图片版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 440.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览


文档简介
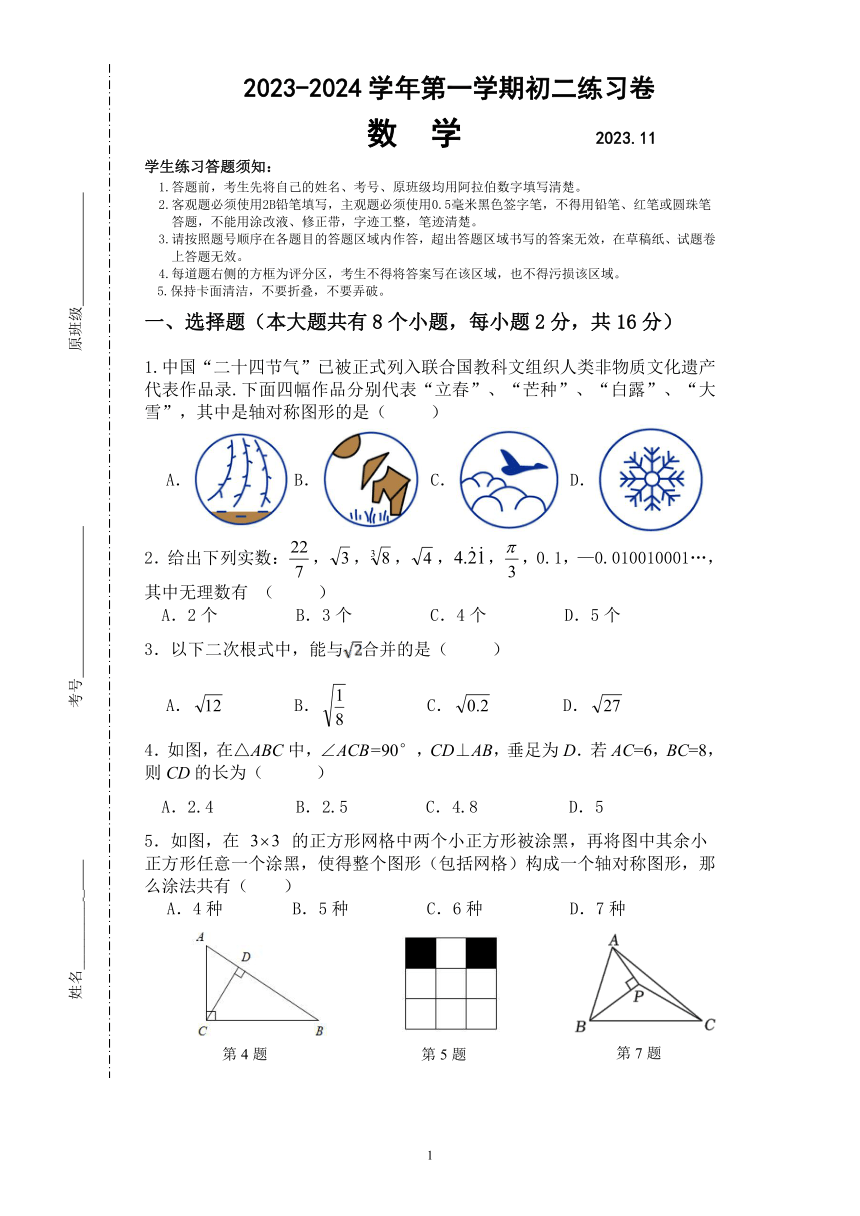
2023-2024 学年第一学期初二练习卷
数 学 2023.11
学生练习答题须知:
1.答题前,考生先将自己的姓名、考号、原班级均用阿拉伯数字填写清楚。
2.客观题必须使用2B铅笔填写,主观题必须使用0.5毫米黑色签字笔,不得用铅笔、红笔或圆珠笔
答题,不能用涂改液、修正带,字迹工整,笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷
上答题无效。
4.每道题右侧的方框为评分区,考生不得将答案写在该区域,也不得污损该区域。
5.保持卡面清洁,不要折叠,不要弄破。
一、选择题(本大题共有 8 个小题,每小题 2 分,共 16 分)
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产
代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大
雪”,其中是轴对称图形的是( )
A. B. C. D.
22
2.给出下列实数: , 3,3 8, 4 ,4.2 1 , ,0.1,—0.010010001…,
7 3
其中无理数有 ( )
A.2个 B.3个 C.4个 D.5个
3.以下二次根式中,能与 合并的是( )
A. 12 1B. C. 0.2 D. 27
8
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为 D.若 AC=6,BC=8,
则 CD的长为( )
A.2.4 B.2.5 C.4.8 D.5
5.如图,在 3 3 的正方形网格中两个小正方形被涂黑,再将图中其余小
正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那
么涂法共有( )
A.4种 B.5种 C.6种 D.7种
第 4题 第 5题 第 7题
1
姓名_________ _ 考号 原班级
6.在△ABC中以下条件能判定△ABC是直角三角形的个数有( )个
条件①:∠A=∠C-∠B;
条件②:三角形三边 a,b,c的比 3:4:5;
条件③:∠A:∠B:∠C=3:1:5;
条件④:a=5、b=12、c=13.
条件⑤:三角形三边 a,b,c满足 b2=a2-c2
A.2 B.3 C.4 D.5 第 8题
2
7.如图,已知 BP是∠ABC的平分线,AP⊥BP,若 S△BPC=10cm ,则△ABC
的面积等于 ( )
2 2 2
A.20cm B.30cm C.25cm D.不能确定
8.如图,在△ABC中,∠BAC=60°,∠BAC的平分线 AD与边 BC的垂直
平分线相交于点 D,DE⊥AB交 AB的延长线于点 E,DF⊥AC于点 F,现有
下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;
其中正确的有( )
A.2个 B.3个 C.4个 D.1个
二、填空题(本大题共有 8 个小题,每小题 2 分,共 16 分)
9.式子 2x 3 成立的条件是 .
10.81 的平方根是 .
11.若等腰三角形的周长为 16cm,其中一边长为 4cm,则该等腰三角形的底边
长为 cm.
12.如图,DE是△ABC的边 AB的垂直平分线,垂足为点 D,DE交 AC于
点 E,且 AC=9,△BEC的周长为 14,则 BC的长为 .
第 12题 第 13题 第 14题
13. 如图,正方形 ABCD的边长为 4,点 F在线段 AD上,AF=1,点 E在线
段 CD上,连接 EF,此时∠AFB=∠EFB,则 DE的长度为__________.
14.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合 2寸,
问门广几何?”意思是:如图推开两扇门( AD和BC),门边沿 D,C两点
到门槛 AB的距高是 1尺(1尺=10 寸),两扇门的间隙CD为 2寸,则门槛
AB长为__________寸. 1
15.如图,在△ABC中,∠A=32°,分别以点 A、C为圆心,大于 2 AC长
为半径画弧,两弧分别相交于点 M、N,直线 MN与 AC相交于点 E,过点 C
作 CD⊥AB,垂足为点 D,CD与 BE相交于点 F,若 BD=CE,则∠BFC的
度数为 .
2
第 15题 第 16题
16.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=4,若 D是 BC边上的
动点,则 2AD+DC的最小值是 .
三、解答题(共 68分)
17.计算(3分):
18. 求下列各式中的 x的值:(每小题 3分,共 6分)
(1)5x2 10 0 (2)3 x 3 4 375
19. (6 分)已知5a 2的立方根是 3,3a b 1的算术平方根是 4,c是 13的
整数部分.
(1)求 a,b,c的值;
(2)求3a b c的平方根.
20. (6 分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF 的对称轴 l;
(2)结合所画图形,在直线 l上画出点 P,使 PA+PC最小;
(3)如果每一个小正方形的边长为 1,请直接写出 ABC的面
积=______.
21.(4分)图 1、图 2是两张形状、大小完全相同的方格纸,
方格纸的每个小正方形的边长均为1,点 A,B在小正方形的顶点上.
(1)在图 1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角
形,并且面积为4;(画一个即可)
(2)在图 2中画出△ABC(点C在小正方形的顶点上),使△ABC为钝角三角
形,并且面积为4.(画一个即可)
3
22.(6分)如图,公路上 A、B两点相距 50km,C、D为两村庄,DA AB于
A,CB AB于 B,已知DA 30km,CB 20km,现在要在公路 AB上建一个土
特产品市场 E,使得C、D两村庄到市场 E的距离相等,则市场 E应建在距 A
多少千米处 并判断此时△DEC的形状,请说明
理由.
23.(6 分)如图,在四边形 ABCD中,AB=5,AD=AC=12,
BAD BCD 90 .M、N分别是对角线 BD,AC的中点.
(1)请判断 MN和 AC的位置关系,并证明;
(2)求线段 MN的长.
24.(8分)定义:用一条直线分割一个三角形,如果能分割出等腰三角形,
那么就称这条直线为该三角形的一条等腰分割线.
如图,Rt△ABC中, ACB 90 .
(1)如图(1),若 O为 AB的中点,则直线 OC_____△ABC的等腰分割线.(填
“是”或“不是”)
(2)如图(2)已知△ABC的一条等腰分割线 BP交边 AC于点 P,且 PB=PA,
若∠A=40°,请求出∠PBC的度数.
(3)如图(3),若 AC=4,BC=3,点 M是边 AB上的一点,如果直线 CM是
△ABC的等腰分割线,这样的点 M共有______个.
4
25.(9 分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点
M以 2厘米 秒的速度运动.
如果点 M在线段 CB上由点 C向点 B运动,点 N在线段
BA上由 B点向 A点运动.它们同时出发,若点 N的运动速
度与点 M的运动速度相等.
经过 3秒后,△BMN和△CDM是否全等?请说明理由.
当两点的运动时间为多少时,△BMN是一个直角三角形?
若点 N的运动速度与点 M的运动速度不相等,点 N从点 B出发,点 M以原
来的运动速度从点 C同时出发,都顺时针沿△ABC三边运动,经过 25 秒点 M与
点 N第一次相遇,则点 N的运动速度是______厘米 秒. 直接写出答案
26. (14 分)如图(1),Rt△ABC中,∠ACB=90°,AC=6,BC=8,点 D在 BC
,
边上,将△ABD沿直线 AD翻折,点 B的对应点 B 恰好落在 AC延长线上,
B,连 D.
(1)求 CD的长;
(2)如图(2),点 E在线段 AD BE EB,上,连 , ,BB,,当△EBB,是等腰直
角三角形时
①求证:点 E在∠ACB的平分线上;
②求点 E到 AC边的距离.
(3)如图(3),在(2)的条件下,点 P从点 B出发以每秒 2个单位长度的速
度沿 BC往点 C运动,连 PE,过点 E作 EP的垂线,交直线 AC于点 Q,问点 P
运动多少秒时,△AEQ是等腰三角形?
B B B
P
D D
E D E
B, A B
,
B, C A C Q C
A
1 图(2) 图(3)图( )
B B
D
E D E
B, C A B, C A
备用图 备用图
5
数 学 2023.11
学生练习答题须知:
1.答题前,考生先将自己的姓名、考号、原班级均用阿拉伯数字填写清楚。
2.客观题必须使用2B铅笔填写,主观题必须使用0.5毫米黑色签字笔,不得用铅笔、红笔或圆珠笔
答题,不能用涂改液、修正带,字迹工整,笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷
上答题无效。
4.每道题右侧的方框为评分区,考生不得将答案写在该区域,也不得污损该区域。
5.保持卡面清洁,不要折叠,不要弄破。
一、选择题(本大题共有 8 个小题,每小题 2 分,共 16 分)
1.中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产
代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大
雪”,其中是轴对称图形的是( )
A. B. C. D.
22
2.给出下列实数: , 3,3 8, 4 ,4.2 1 , ,0.1,—0.010010001…,
7 3
其中无理数有 ( )
A.2个 B.3个 C.4个 D.5个
3.以下二次根式中,能与 合并的是( )
A. 12 1B. C. 0.2 D. 27
8
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为 D.若 AC=6,BC=8,
则 CD的长为( )
A.2.4 B.2.5 C.4.8 D.5
5.如图,在 3 3 的正方形网格中两个小正方形被涂黑,再将图中其余小
正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那
么涂法共有( )
A.4种 B.5种 C.6种 D.7种
第 4题 第 5题 第 7题
1
姓名_________ _ 考号 原班级
6.在△ABC中以下条件能判定△ABC是直角三角形的个数有( )个
条件①:∠A=∠C-∠B;
条件②:三角形三边 a,b,c的比 3:4:5;
条件③:∠A:∠B:∠C=3:1:5;
条件④:a=5、b=12、c=13.
条件⑤:三角形三边 a,b,c满足 b2=a2-c2
A.2 B.3 C.4 D.5 第 8题
2
7.如图,已知 BP是∠ABC的平分线,AP⊥BP,若 S△BPC=10cm ,则△ABC
的面积等于 ( )
2 2 2
A.20cm B.30cm C.25cm D.不能确定
8.如图,在△ABC中,∠BAC=60°,∠BAC的平分线 AD与边 BC的垂直
平分线相交于点 D,DE⊥AB交 AB的延长线于点 E,DF⊥AC于点 F,现有
下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE;
其中正确的有( )
A.2个 B.3个 C.4个 D.1个
二、填空题(本大题共有 8 个小题,每小题 2 分,共 16 分)
9.式子 2x 3 成立的条件是 .
10.81 的平方根是 .
11.若等腰三角形的周长为 16cm,其中一边长为 4cm,则该等腰三角形的底边
长为 cm.
12.如图,DE是△ABC的边 AB的垂直平分线,垂足为点 D,DE交 AC于
点 E,且 AC=9,△BEC的周长为 14,则 BC的长为 .
第 12题 第 13题 第 14题
13. 如图,正方形 ABCD的边长为 4,点 F在线段 AD上,AF=1,点 E在线
段 CD上,连接 EF,此时∠AFB=∠EFB,则 DE的长度为__________.
14.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合 2寸,
问门广几何?”意思是:如图推开两扇门( AD和BC),门边沿 D,C两点
到门槛 AB的距高是 1尺(1尺=10 寸),两扇门的间隙CD为 2寸,则门槛
AB长为__________寸. 1
15.如图,在△ABC中,∠A=32°,分别以点 A、C为圆心,大于 2 AC长
为半径画弧,两弧分别相交于点 M、N,直线 MN与 AC相交于点 E,过点 C
作 CD⊥AB,垂足为点 D,CD与 BE相交于点 F,若 BD=CE,则∠BFC的
度数为 .
2
第 15题 第 16题
16.如图,在△ABC中,∠BAC=90°,∠B=60°,AB=4,若 D是 BC边上的
动点,则 2AD+DC的最小值是 .
三、解答题(共 68分)
17.计算(3分):
18. 求下列各式中的 x的值:(每小题 3分,共 6分)
(1)5x2 10 0 (2)3 x 3 4 375
19. (6 分)已知5a 2的立方根是 3,3a b 1的算术平方根是 4,c是 13的
整数部分.
(1)求 a,b,c的值;
(2)求3a b c的平方根.
20. (6 分)如图,网格中的△ABC与△DEF为轴对称图形.
(1)利用网格线作出△ABC与△DEF 的对称轴 l;
(2)结合所画图形,在直线 l上画出点 P,使 PA+PC最小;
(3)如果每一个小正方形的边长为 1,请直接写出 ABC的面
积=______.
21.(4分)图 1、图 2是两张形状、大小完全相同的方格纸,
方格纸的每个小正方形的边长均为1,点 A,B在小正方形的顶点上.
(1)在图 1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角
形,并且面积为4;(画一个即可)
(2)在图 2中画出△ABC(点C在小正方形的顶点上),使△ABC为钝角三角
形,并且面积为4.(画一个即可)
3
22.(6分)如图,公路上 A、B两点相距 50km,C、D为两村庄,DA AB于
A,CB AB于 B,已知DA 30km,CB 20km,现在要在公路 AB上建一个土
特产品市场 E,使得C、D两村庄到市场 E的距离相等,则市场 E应建在距 A
多少千米处 并判断此时△DEC的形状,请说明
理由.
23.(6 分)如图,在四边形 ABCD中,AB=5,AD=AC=12,
BAD BCD 90 .M、N分别是对角线 BD,AC的中点.
(1)请判断 MN和 AC的位置关系,并证明;
(2)求线段 MN的长.
24.(8分)定义:用一条直线分割一个三角形,如果能分割出等腰三角形,
那么就称这条直线为该三角形的一条等腰分割线.
如图,Rt△ABC中, ACB 90 .
(1)如图(1),若 O为 AB的中点,则直线 OC_____△ABC的等腰分割线.(填
“是”或“不是”)
(2)如图(2)已知△ABC的一条等腰分割线 BP交边 AC于点 P,且 PB=PA,
若∠A=40°,请求出∠PBC的度数.
(3)如图(3),若 AC=4,BC=3,点 M是边 AB上的一点,如果直线 CM是
△ABC的等腰分割线,这样的点 M共有______个.
4
25.(9 分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点
M以 2厘米 秒的速度运动.
如果点 M在线段 CB上由点 C向点 B运动,点 N在线段
BA上由 B点向 A点运动.它们同时出发,若点 N的运动速
度与点 M的运动速度相等.
经过 3秒后,△BMN和△CDM是否全等?请说明理由.
当两点的运动时间为多少时,△BMN是一个直角三角形?
若点 N的运动速度与点 M的运动速度不相等,点 N从点 B出发,点 M以原
来的运动速度从点 C同时出发,都顺时针沿△ABC三边运动,经过 25 秒点 M与
点 N第一次相遇,则点 N的运动速度是______厘米 秒. 直接写出答案
26. (14 分)如图(1),Rt△ABC中,∠ACB=90°,AC=6,BC=8,点 D在 BC
,
边上,将△ABD沿直线 AD翻折,点 B的对应点 B 恰好落在 AC延长线上,
B,连 D.
(1)求 CD的长;
(2)如图(2),点 E在线段 AD BE EB,上,连 , ,BB,,当△EBB,是等腰直
角三角形时
①求证:点 E在∠ACB的平分线上;
②求点 E到 AC边的距离.
(3)如图(3),在(2)的条件下,点 P从点 B出发以每秒 2个单位长度的速
度沿 BC往点 C运动,连 PE,过点 E作 EP的垂线,交直线 AC于点 Q,问点 P
运动多少秒时,△AEQ是等腰三角形?
B B B
P
D D
E D E
B, A B
,
B, C A C Q C
A
1 图(2) 图(3)图( )
B B
D
E D E
B, C A B, C A
备用图 备用图
5
同课章节目录
