青岛版九年级数学上册 3.4.4切线长定理课件 14张PPT
文档属性
| 名称 | 青岛版九年级数学上册 3.4.4切线长定理课件 14张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 11:25:47 | ||
图片预览





文档简介
(共14张PPT)
3.4.4切线长定理
2
学习目标
1.了解切线长的概念。
2、能证明切线长定理,并能用切线长定理进行计算和证明.
切线的性质及判定
复习引入
2.过圆上一点可以作圆的几条切线?那么过圆外一点可以作圆的几条切线呢?
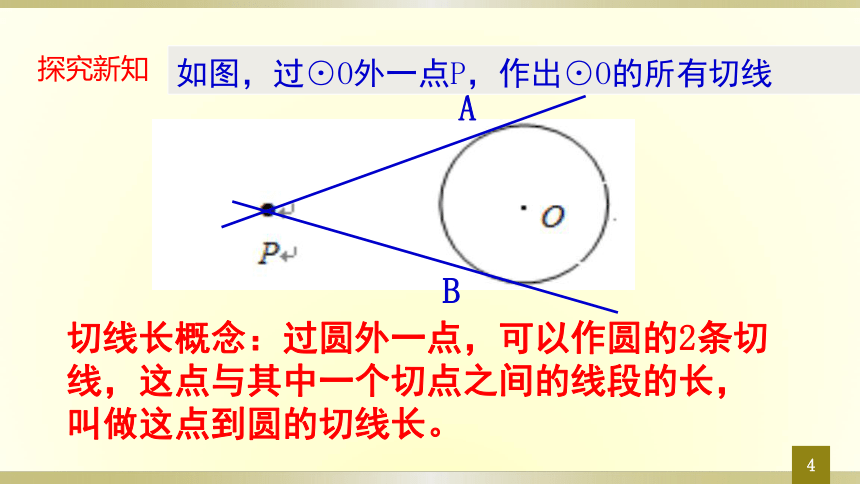
如图,过⊙O外一点P,作出⊙O的所有切线
探究新知
A
B
切线长概念:过圆外一点,可以作圆的2条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长。
思考:切线与切线长是同一个概念吗?
圆的切线是一条直线,是一个图形,切线长则是一条线段的长度,是一个数量。
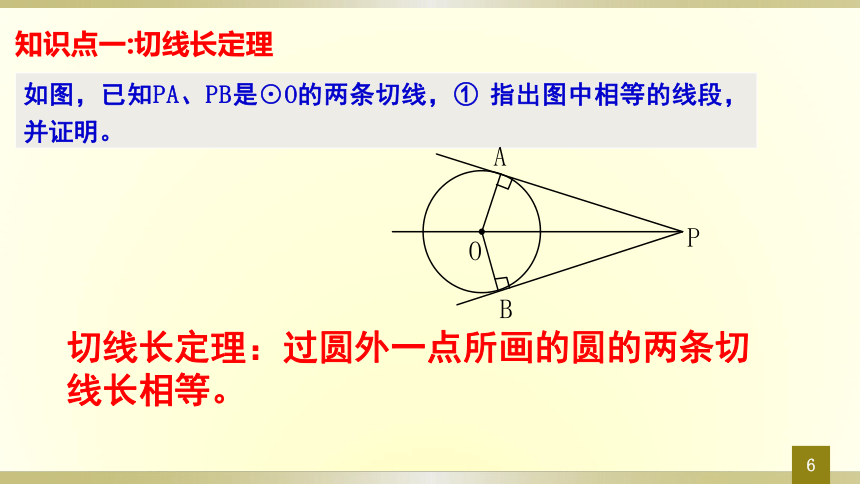
如图,已知PA、PB是⊙O的两条切线,① 指出图中相等的线段,并证明。
知识点一:切线长定理
切线长定理:过圆外一点所画的圆的两条切线长相等。
例4、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A B是切点,BC是⊙O的直径
(1)求证:AC ∥OP:
( 2 )如果∠APB=700,求AC的度数
⌒
A
C
P
B
o
如图,⊙O与△ABC的边BC相切,切点为点D,与AB、AC的延长线相切,切点分别为点E、F,则图中相等的线段有_______________________,若AF=10,则⊿ABC的周长为 ,若⊿ABC的周长
为30,则AF的长为 .
对应练习一
FC=CD,BD=BE,AF=AE
20
15
如图,已知PA、PB是⊙O的两条切线,连接AB交OP于C,
②试找出图中与∠APO相等的角;图中有几条角平分线?
③试找出图中与∠APO互余的角;
④试找出图中与∠APB互补的角;
⑤思考OP与AB的位置关系并证明。
知识点二:切线长定理基本图
C
挑战自我
如图是一个用来测量球形物体直径的V型架,其中PA与PB是经过圆外一点P的两条切线,切点分别是A、B,∠P=60 ,如果一个乒乓球放入V型架里,量的PA=4.5cm,怎样求乒乓球的直径(精确到0.1cm)
P
A
B
O
练习1、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;(2)如果∠APB=70?,求弧AC的度数.
解:连接OA,AB交OP于D.
(1) ∵ PA、PB是切线
∴ PA=PB
又∵ OA=OB
∴OP垂直平分AB
∵BC为直径
∴ ∠CAB=90
∴∠CAB=∠ODB
∴AC∥OP
D
练习1、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;(2)如果∠APB=70?,求弧AC的度数.
解:连接OA,AB交OP于D.
D
(2) ∵ PA、PB是切线
∴∠OAP=∠OBP=90
∴∠BOA=360 -∠OAP-
∠OBP-∠APB=110
∴ ∠COA=70
∴弧AC的度数为70
1. 如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=70°.则∠P=________.
练习二
40?
课堂小结
1、这节课你有哪些收获?
2、学习到了哪些知识?哪些数学方法、思想?
3.4.4切线长定理
2
学习目标
1.了解切线长的概念。
2、能证明切线长定理,并能用切线长定理进行计算和证明.
切线的性质及判定
复习引入
2.过圆上一点可以作圆的几条切线?那么过圆外一点可以作圆的几条切线呢?
如图,过⊙O外一点P,作出⊙O的所有切线
探究新知
A
B
切线长概念:过圆外一点,可以作圆的2条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长。
思考:切线与切线长是同一个概念吗?
圆的切线是一条直线,是一个图形,切线长则是一条线段的长度,是一个数量。
如图,已知PA、PB是⊙O的两条切线,① 指出图中相等的线段,并证明。
知识点一:切线长定理
切线长定理:过圆外一点所画的圆的两条切线长相等。
例4、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A B是切点,BC是⊙O的直径
(1)求证:AC ∥OP:
( 2 )如果∠APB=700,求AC的度数
⌒
A
C
P
B
o
如图,⊙O与△ABC的边BC相切,切点为点D,与AB、AC的延长线相切,切点分别为点E、F,则图中相等的线段有_______________________,若AF=10,则⊿ABC的周长为 ,若⊿ABC的周长
为30,则AF的长为 .
对应练习一
FC=CD,BD=BE,AF=AE
20
15
如图,已知PA、PB是⊙O的两条切线,连接AB交OP于C,
②试找出图中与∠APO相等的角;图中有几条角平分线?
③试找出图中与∠APO互余的角;
④试找出图中与∠APB互补的角;
⑤思考OP与AB的位置关系并证明。
知识点二:切线长定理基本图
C
挑战自我
如图是一个用来测量球形物体直径的V型架,其中PA与PB是经过圆外一点P的两条切线,切点分别是A、B,∠P=60 ,如果一个乒乓球放入V型架里,量的PA=4.5cm,怎样求乒乓球的直径(精确到0.1cm)
P
A
B
O
练习1、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;(2)如果∠APB=70?,求弧AC的度数.
解:连接OA,AB交OP于D.
(1) ∵ PA、PB是切线
∴ PA=PB
又∵ OA=OB
∴OP垂直平分AB
∵BC为直径
∴ ∠CAB=90
∴∠CAB=∠ODB
∴AC∥OP
D
练习1、如图,P为⊙O外一点,PA、PB是⊙O的两条切线,A、B是切点,BC是⊙O的直径.
(1)求证:AC∥OP;(2)如果∠APB=70?,求弧AC的度数.
解:连接OA,AB交OP于D.
D
(2) ∵ PA、PB是切线
∴∠OAP=∠OBP=90
∴∠BOA=360 -∠OAP-
∠OBP-∠APB=110
∴ ∠COA=70
∴弧AC的度数为70
1. 如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=70°.则∠P=________.
练习二
40?
课堂小结
1、这节课你有哪些收获?
2、学习到了哪些知识?哪些数学方法、思想?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
