青岛版九年级数学第3章3.7正多边形与圆的关系(1) 课件(29张PPT)
文档属性
| 名称 | 青岛版九年级数学第3章3.7正多边形与圆的关系(1) 课件(29张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
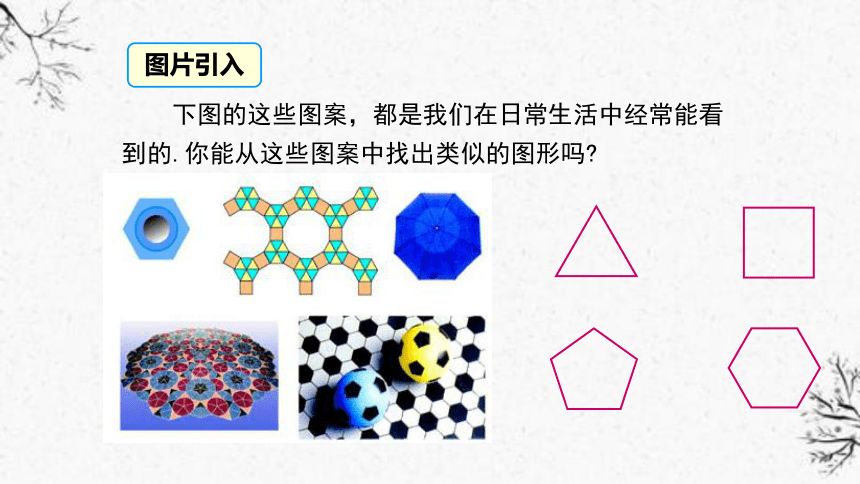
下图的这些图案,都是我们在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗
图片引入
3.7 正多边形与圆
1. 了解正多边形的中心、半径、边心距、中心角等概念,了解正多边形与圆的关系。
2. 探索正多边形的性质,能利用正多边形的性质进行有关的计算。
3.了解画正多边形的方法,会用基本作图作圆的内接正方形和正六边形。
学习目标
正多边形的概念及相关计算
一
观察下面多边形,它们的边、角有什么特点?
各边相等,各内角也相等.
观察与思考
知识要点
各边相等,各内角也相等的多边形叫做正多边形.
正多边形
各边相等
各角相等
缺一不可
如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
思考:
菱形是正多边形吗 矩形是正多边形呢
正多边形的对称性
一
(1)它们是轴对称图形吗?如果是,它们有几条对称轴?各条对称轴有怎样的特征?
3
4
5
6
归纳:正多边形都是轴对称图形,一个正n边形共有n条对称轴。
正多边形各条对称轴相交于一点,这点到正多边形各个
顶点的距离相等,到各边的距离也相等。
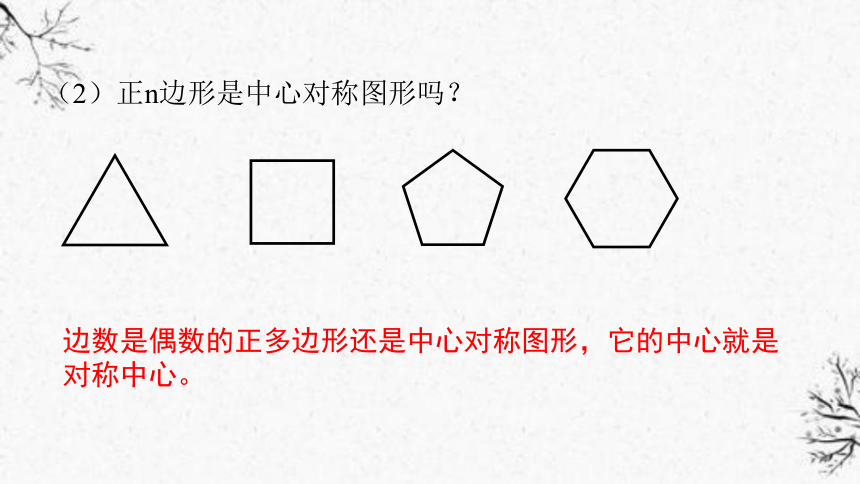
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
(2)正n边形是中心对称图形吗?
B
A
C
D
E
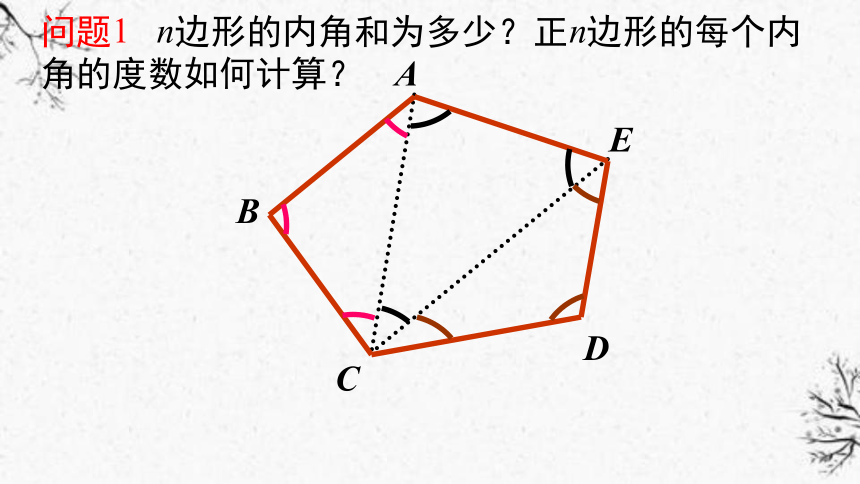
问题1 n边形的内角和为多少?正n边形的每个内角的度数如何计算?
B
A
C
D
G
F
E
n边形的内角和为
正n边形的每个内角的度数为
n边形外角和=
n个平角-n边形内角和
问题2 n边形的外角和为多少?已知正n边形的内角为a度,如何求n的值?
6
E
B
C
D
1
2
3
4
5
A
n边形外角和=
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
问题2 n边形的外角和为多少?已知正n边形的内角为a度,如何求n的值?
n边形的外角和为360°
正n边形的每一个外角:
1.若一个正n边形的每个内角为144°,则这个正n边形的是正____边形.
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
十
练一练
C
正多边形有没有外接圆?
任何正多边形都有一个外接圆和一个内切圆,这两个圆是
同心圆,圆心是各对称轴的交点。
正多边形与圆
三
有没有内切圆?
它们的圆心有
什么样的特征?
O
O
O
O
O
如图,一个正六边形和它的外接圆、内切圆:
一个正多边形的外接圆和内切圆的公共圆心叫做正多边形的中心。
E
F
C
D
.
O
A
B
2、外接圆的半径叫
做正多边形的半径。
O
A
B
C
D
E
F
3、内切圆的半径叫
做正多边形的边心距。
E
F
C
D
.
O
A
B
4、正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角。
O
A
B
C
D
E
F
正n边形的中心角:
E
F
C
D
.
O
中心角
半径
边心距
正多边形的内角:
正多边形的半径:
正多边形的中心角:
A
B
正多边形的面积:
外接圆的半径
正多边形的边长、边心距和半径的关系:
M
正多边形的边心距:
内切圆的半径
5.如图,边AB是圆O内接正六边形的一边,点C在 上,
且BC是圆O内接正八边形的一边,若AC是圆O内接正n边形的一边,则n= 。
练一练
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( ).
A. 4 B. 5 C. 6 D. 7
B
2.边长为a的正六边形的内切圆的半径为( )
A.2a B.a C. a D. a
3.用一张圆形的纸剪一个边长为4 cm的正六边形,则这个圆形纸片的半径最小应为_______cm.
1.正六边形内接与圆,它的边所对的圆周角是( )
A. 60 0 B. 1200 C.600或1200 D.300或1500
2.边长为10的正六边形的边心距为 .
例1
一个正六边形花坛的半径为R,求花坛的边长a,周长p和面积S.
2.有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积.
面积
2.如图,六边形ABCDEF为圆O的内接正六边形, ,则图中阴影部分的面积是( )
A. B.
C. D.
例2 利用尺规作图,作出已知圆的内接正方形和内接正六边形.
解:内接正方形的做法:
(1)用直尺作圆的一条直径AC;
A
C
O
(2)作与AC垂直的直径BD;
B
D
(3)顺次连接所得的圆上四点.
四边形ABCD即为所求作的正方形.
再逐次平分各边所对的弧,就可以作出正八边形、正十六边型等.
正多边形的画法
四
O
解:内接正六方形的做法:
(1)用直尺作圆的一条直径AD;
(2)以点A为圆心,OA为半径作圆,
与⊙O交于点B、F;
(4)顺次连接所得的圆上六点.
六边形ABCDEF即为所求作的正六边形.
A
D
B
F
(3)以点D为圆心,OD为半径作圆,
与⊙O交与点C、E.
C
E
如果再逐次等分各边所对的弧,就可以作出正十二边形、正二十四边型等.
方法归纳:用等分圆周的方法作正多边形:①用量角
器等分圆周;②用尺规等分圆周(特殊正n边形).
课堂检测
2.边长为a的正六边形的内切圆的半径为( )
A.2a B.a C. a D. a
1.下列说法错误的是( )
A.圆内接正n边形的中心角为
B.各边相等,各角也相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的多边形是正多边形
D
C
4.如图,正六边形ABCDE内接于圆O,若直线PA与圆O相切于点A,则的度数为 。
课堂小结
正多边形与圆
正多边形
正多边形与圆的关系
各边相等
各角相等
缺一不可
内接正多边形
外切正多边形
下图的这些图案,都是我们在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗
图片引入
3.7 正多边形与圆
1. 了解正多边形的中心、半径、边心距、中心角等概念,了解正多边形与圆的关系。
2. 探索正多边形的性质,能利用正多边形的性质进行有关的计算。
3.了解画正多边形的方法,会用基本作图作圆的内接正方形和正六边形。
学习目标
正多边形的概念及相关计算
一
观察下面多边形,它们的边、角有什么特点?
各边相等,各内角也相等.
观察与思考
知识要点
各边相等,各内角也相等的多边形叫做正多边形.
正多边形
各边相等
各角相等
缺一不可
如果一个正多边形有n条边,那么这个正多边形叫做正n边形.
思考:
菱形是正多边形吗 矩形是正多边形呢
正多边形的对称性
一
(1)它们是轴对称图形吗?如果是,它们有几条对称轴?各条对称轴有怎样的特征?
3
4
5
6
归纳:正多边形都是轴对称图形,一个正n边形共有n条对称轴。
正多边形各条对称轴相交于一点,这点到正多边形各个
顶点的距离相等,到各边的距离也相等。
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
(2)正n边形是中心对称图形吗?
B
A
C
D
E
问题1 n边形的内角和为多少?正n边形的每个内角的度数如何计算?
B
A
C
D
G
F
E
n边形的内角和为
正n边形的每个内角的度数为
n边形外角和=
n个平角-n边形内角和
问题2 n边形的外角和为多少?已知正n边形的内角为a度,如何求n的值?
6
E
B
C
D
1
2
3
4
5
A
n边形外角和=
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
问题2 n边形的外角和为多少?已知正n边形的内角为a度,如何求n的值?
n边形的外角和为360°
正n边形的每一个外角:
1.若一个正n边形的每个内角为144°,则这个正n边形的是正____边形.
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
十
练一练
C
正多边形有没有外接圆?
任何正多边形都有一个外接圆和一个内切圆,这两个圆是
同心圆,圆心是各对称轴的交点。
正多边形与圆
三
有没有内切圆?
它们的圆心有
什么样的特征?
O
O
O
O
O
如图,一个正六边形和它的外接圆、内切圆:
一个正多边形的外接圆和内切圆的公共圆心叫做正多边形的中心。
E
F
C
D
.
O
A
B
2、外接圆的半径叫
做正多边形的半径。
O
A
B
C
D
E
F
3、内切圆的半径叫
做正多边形的边心距。
E
F
C
D
.
O
A
B
4、正多边形每一边所对的外接圆的圆心角叫做正多边形的中心角。
O
A
B
C
D
E
F
正n边形的中心角:
E
F
C
D
.
O
中心角
半径
边心距
正多边形的内角:
正多边形的半径:
正多边形的中心角:
A
B
正多边形的面积:
外接圆的半径
正多边形的边长、边心距和半径的关系:
M
正多边形的边心距:
内切圆的半径
5.如图,边AB是圆O内接正六边形的一边,点C在 上,
且BC是圆O内接正八边形的一边,若AC是圆O内接正n边形的一边,则n= 。
练一练
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( ).
A. 4 B. 5 C. 6 D. 7
B
2.边长为a的正六边形的内切圆的半径为( )
A.2a B.a C. a D. a
3.用一张圆形的纸剪一个边长为4 cm的正六边形,则这个圆形纸片的半径最小应为_______cm.
1.正六边形内接与圆,它的边所对的圆周角是( )
A. 60 0 B. 1200 C.600或1200 D.300或1500
2.边长为10的正六边形的边心距为 .
例1
一个正六边形花坛的半径为R,求花坛的边长a,周长p和面积S.
2.有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面积.
面积
2.如图,六边形ABCDEF为圆O的内接正六边形, ,则图中阴影部分的面积是( )
A. B.
C. D.
例2 利用尺规作图,作出已知圆的内接正方形和内接正六边形.
解:内接正方形的做法:
(1)用直尺作圆的一条直径AC;
A
C
O
(2)作与AC垂直的直径BD;
B
D
(3)顺次连接所得的圆上四点.
四边形ABCD即为所求作的正方形.
再逐次平分各边所对的弧,就可以作出正八边形、正十六边型等.
正多边形的画法
四
O
解:内接正六方形的做法:
(1)用直尺作圆的一条直径AD;
(2)以点A为圆心,OA为半径作圆,
与⊙O交于点B、F;
(4)顺次连接所得的圆上六点.
六边形ABCDEF即为所求作的正六边形.
A
D
B
F
(3)以点D为圆心,OD为半径作圆,
与⊙O交与点C、E.
C
E
如果再逐次等分各边所对的弧,就可以作出正十二边形、正二十四边型等.
方法归纳:用等分圆周的方法作正多边形:①用量角
器等分圆周;②用尺规等分圆周(特殊正n边形).
课堂检测
2.边长为a的正六边形的内切圆的半径为( )
A.2a B.a C. a D. a
1.下列说法错误的是( )
A.圆内接正n边形的中心角为
B.各边相等,各角也相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的多边形是正多边形
D
C
4.如图,正六边形ABCDE内接于圆O,若直线PA与圆O相切于点A,则的度数为 。
课堂小结
正多边形与圆
正多边形
正多边形与圆的关系
各边相等
各角相等
缺一不可
内接正多边形
外切正多边形
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
