高一(下)数学(必修③人教A版)第一章:算法初步(学案)(安徽省巢湖地区)
文档属性
| 名称 | 高一(下)数学(必修③人教A版)第一章:算法初步(学案)(安徽省巢湖地区) |  | |
| 格式 | rar | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-16 09:25:00 | ||
图片预览


文档简介
高一(下)数学(必修③·人教A版)第一章:算法初步(学案)
§1.1.1算法的概念
1、 基础梳理
1、算法的概念:在数学中,算法通常是指 。现在,算法通常可以编成 ,让计算机执行并解决问题。
2.计算机解决任何问题都依赖于算法,只有将解决问题的过程 ,并用计算机能够接受的“语言” ,计算机才能够 。
2、 合作探究
1、 你能举出更多的算法的例子吗?
2、 与一般的解决问题的过程相比,你认为算法最重要的特征是什么?
3、 自学检测
1、 跟根据算法的思想,用自然语言写出烧开水的过程。
2、 下列关于算法的说法中,,正确的有( )
①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是清楚的,不能有歧义;④算法执行后一定产生确定的结果.
A.1个 B.2个 C.3个 D.4个
3、现在河的岸边有三头牛和三只虎要过河,它们都会划船,只有一条船,船上一次只能载它们其中的两个,虎数大于牛数则虎就要吃牛,两者数目相等或是牛数大于虎数便相安无事。 设计安全渡河的算法。
4、 学生反馈
§1.1.1程序框图(第一课时)
一、基础梳理
1、完成下列表格:
图形符号 名称 功能
起止框(终端框) 表示一个算法的起始和结束
输入输出框 表示一个算法输入和输出的信息
处理框(执行框) 赋值、计算
判断框 判断某一条件是否成立,它有两个出口:“是”或“否”。条件成立时,程序沿着“是”这个分支走下去;当条件不成立时,程序沿着“否”这个分支进行。
流程线 连接程序框
连接点 当一个程序框图很大,一页纸写不下时,用来连接程序框图的两部分。一般在连接处标上相同的数字序号。
2、程序框图又称 ,是一种用 来表示算法的图形。
3、尽管算法千差万别,但它们都是由 、 、 这三种基本的逻辑结构构成的。
1、
二、合作探究
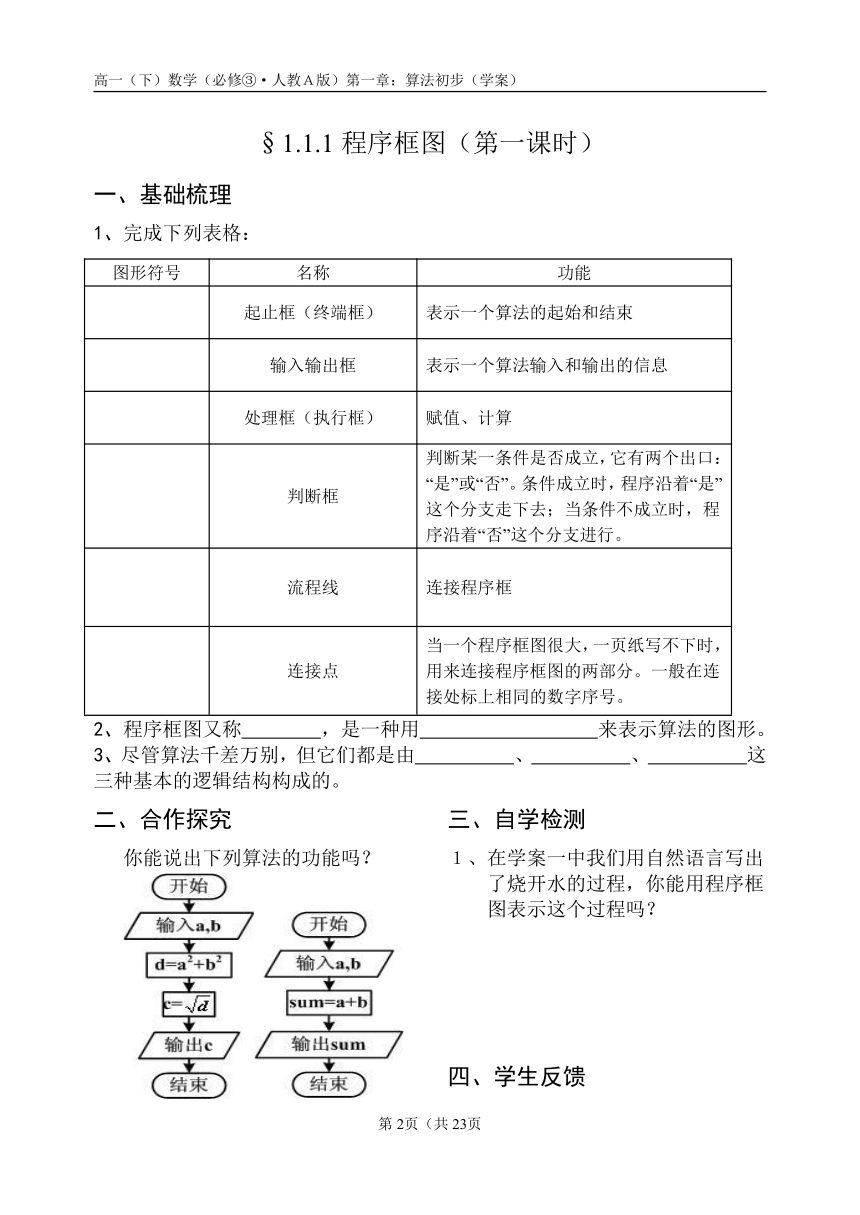
你能说出下列算法的功能吗?
三、自学检测
1、 在学案一中我们用自然语言写出了烧开水的过程,你能用程序框图表示这个过程吗?
四、学生反馈
2、
§1.1.1程序框图(第二课时)
一、基础梳理
1、在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件 有不同的流向,这种先根据条件做出判断,再决定执行哪种操作的结构叫 。
2、条件结构在程序框图中用判断框来表示,在判断框内写上条件,它有 个出口。
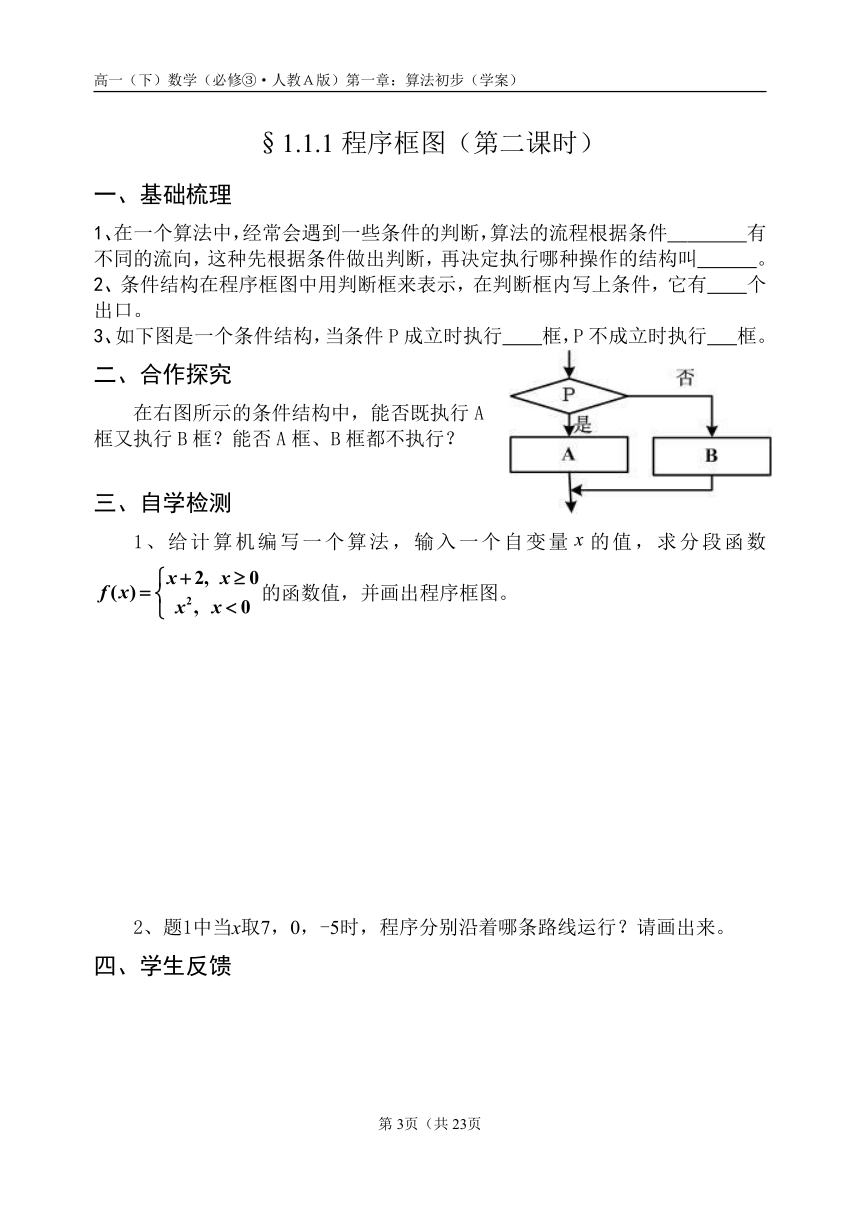
3、如下图是一个条件结构,当条件P成立时执行 框,P不成立时执行 框。
二、合作探究
在右图所示的条件结构中,能否既执行A框又执行B框?能否A框、B框都不执行?
三、自学检测
1、给计算机编写一个算法,输入一个自变量的值,求分段函数的函数值,并画出程序框图。
2、题1中当x取7,0,-5时,程序分别沿着哪条路线运行?请画出来。
四、学生反馈
§1.1.1程序框图(第三课时)
一、基础梳理
1、当型型循环结构在执行循环体之 ,对循环条件进行判断,当条件 时执行循环体, 时则停止循环,执行循环结构后面的步骤。
2、直到型循环结构在 之后,对循环条件进行判断,当条件 时执行循环体, 则停止循环,执行循环结构后面的步骤。
3、试说明计数变量和累加变量的作用。
二、合作探究
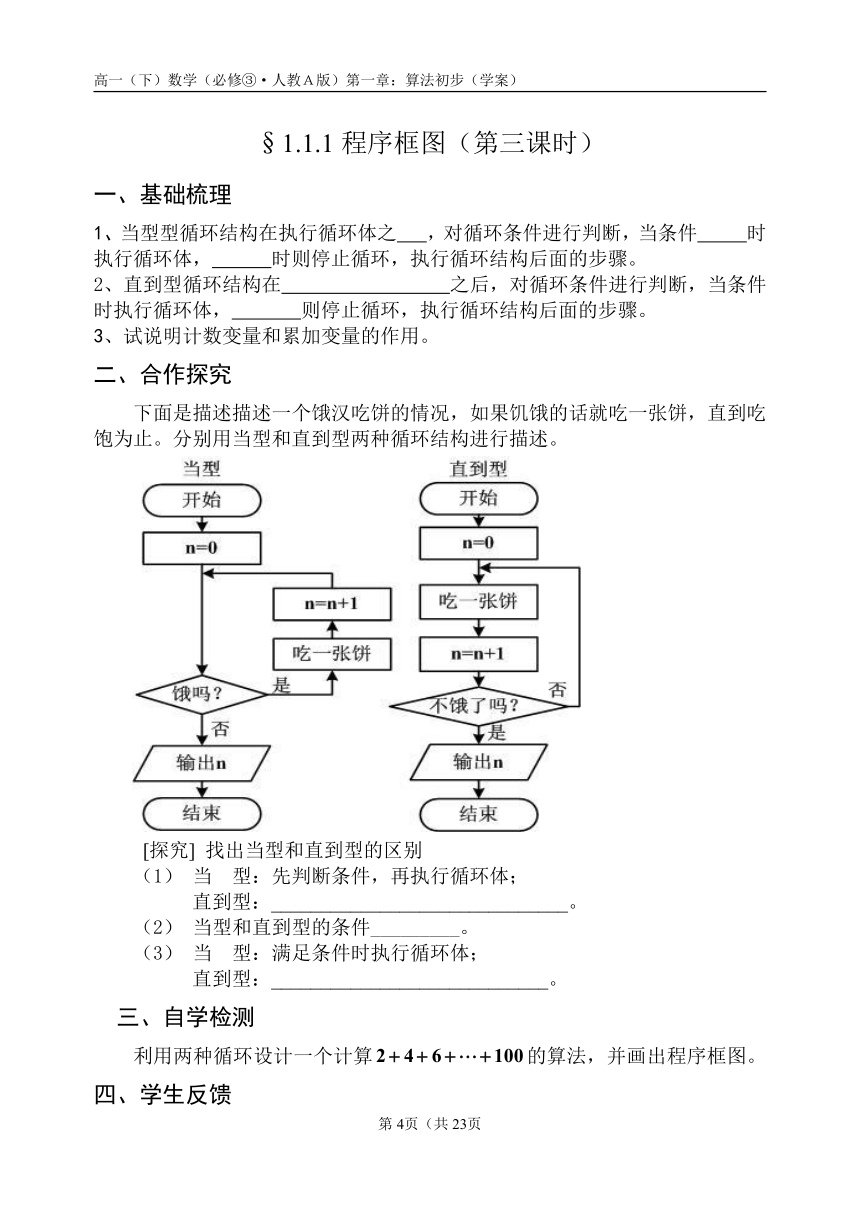
下面是描述描述一个饿汉吃饼的情况,如果饥饿的话就吃一张饼,直到吃饱为止。分别用当型和直到型两种循环结构进行描述。
[探究] 找出当型和直到型的区别
(1) 当 型:先判断条件,再执行循环体;
直到型:______________________________。
(2) 当型和直到型的条件_________。
(3) 当 型:满足条件时执行循环体;
直到型:____________________________。
三、自学检测
利用两种循环设计一个计算的算法,并画出程序框图。四、学生反馈
§1.2.1输入、输出语句和赋值语句(第一课时)
一、基础梳理
1、输入语句的一般格式:
2、输出语句的一般格式:
3、赋值语句的一般格式:
注意标点哦!
附:程序中常用符号
函数名 算术运算符
符号 LOG(x) SQR(x) ABS(x) ^ *,/ MOD,\ +,-
作用 lg(x) |x| 乘方 乘法,除法 求余数,求商 加法,减法
关系运算符 逻辑运算符
符号 = < > >= <= < , > AND OR NOT
作用 赋值 小于,大于 且 或 非
二、合作探究
1、“变量”和“表达式”有什么联系和区别?
2、你是怎么理解赋值语句中的“=”号的,它与“等于”号一样吗?
三、自学检测
1、已知y=x2-3x+1,编写程序,根据输入的x计算并输出y值。
四、学生反馈
课题:1.2.2条件语句(第二课时)
一、基础梳理
1、条件语句的一般格式:(实线框中填语句,虚线框中画框图)
IF-THEN-ELSE格式
IF-THEN格式
二、合作探究
条件结构中,有两个分支,能否两个分支都执行或两个分支都不执行?
三、自学检测
1、编写一个程序,输入3个数,找出其中最大的1个并输出。
四、学生反馈
课题:1.2.3循环语句(第三课时)
一、基础梳理
1、算法中的循环结构是由循环语句来实现的。对应于程序框图中的两种循环结构,一般程序设计语言中也有 型( 型)和 ( 型)两种语句结构。即WHILE语句和UNTIL语句。
(1)WHILE语句的一般格式是:(实线框中填语句,虚线框中画框图)
(2)UNTIL语句的一般格式是:
二、合作探究
试说明WHILE型循环与UNTIL型循环的区别和联系。
三、自学检测
1、设计一个计算的算法,画出程序框图,写出程序。
2、设计一个算法,求的值.,画出程序框图,写出程序。
四、学生反馈
课题:§1.3算法案例(第一课时)
一、基础梳理
1、辗转相除法是用于求 。它是由欧几里德在公元前300年左右首先提出的,因而又叫欧几里德算法。
2、所谓辗转相除法,就是对于给定的两个数,用 除以 。若余数不为零,则将 构成一对新数,继续上面的除法,直到大数被小数除尽,则这时 就是原来两个数的最大公约数。
二、合作探究
用当型循环结构构造算法,求两个正整数的最大公约数吗?试写出算法步骤、程序框图各程序。
三、自学检测
1、转相除法求下列各组数的最大公约数,并在自己编写的BASIC程序中验证。
(1)225;135 (2)98;196 (3)72;168 (4)153;119
四、学生反馈
课题:§1.3算法案例(第二课时)
一、基础梳理
1、更相减损术是我国古代数学专著 中介绍的一种求两个数的最大公约数的方法.其步骤是:第一步,任意给定两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步;第二步,以 ,接着把所得的 与 比较,并以大数减小数.继续这个操作,直到所得的数 为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数。
二、合作探究
把更相减损术与辗转相除法比较,你有什么发现?你能根据更相减损术设计程序,求两个正整数的最大公约数吗?
三、自学检测
1、用更相减损术求294与84最大公约数。
2、分别用辗转相除法和更相减损术求228与1995的最大公约数。
四、学生反馈
课题:§1.3算法案例(第三课时)
一、基础梳理
1、秦九韶算法是我国南宋数学家 在他的代表作 中提出的一种用于计算一元n次多项式的值的算法。
二、合作探究
用秦九韶算法求n次多项式当(是任意实数)时的值,需要多少次乘法运算,多少次加法运算?
三、自学检测
1、利用秦九韶算法计算
当时的值,并统计需要多少次乘法计算和多少次加法计算?
四、学生反馈
课题:§1.3算法案例(第四课时)
一、基础梳理
1、进位制是人们为了计数和运算方便而约定的记数系统.“满几进一”就是 ,几进制的基数就是
2、将k进制数化为十进制数的算法是:先把k进制数写成 的形式,再 .
3、将十进制数化为k进制数的算法是 ,即 ,直到商为零为止,然后 就是相应的k进制数.
二、合作探究
若表示一个k进制数,请你把它写成各位上数字与k的幂的乘积之和的形式。
三、自学检测
1、完成下列进位制的转化
①将十进制数4095化为七进制数;
②将21043(5)转化为十进制数。
2、将八进制数74(8)转化为二进制数。
四、学生反馈
第一章 算法初步测试题(A组)
一、选择题 (每小题5分,共50分)
1.已知直角三角形两直角边长为,,求斜边长的一个算法分下列三步:
①计算;②输入直角三角形两直角边长,的值;
③输出斜边长的值,其中正确的顺序是 ( )
A.①②③ B.②③① C.①③② D.②①③
2.给出以下一个算法的程序框图(如下图所示),该程序框图的功能是 ( )
A.求输出三数的最大数 B.求输出三数的最小数
C.将按从小到大排列 D.将按从大到小排列
3.右边的程序框图,能判断任意输入的数的奇偶性:其中判断框内的条件是( )
A. B. C. D.
4.将两个数=8,=7交换,使=7,=8,使用赋值语句正确的一组 ( )
A. B.
C. =,= D. =,=,=
5.下列给出的输入语句、输出语句和赋值语句
⑴输出语句INPUT ;; (2)输入语句INPUT =3
(3)赋值语句3=B (4)赋值语句A=B=2
则其中正确的个数是, ( )
A.0个 B. 1个 C. 2个 D. 3个
6.直到型循环结构为 ( )
7.下边程序执行后输出的结果是 ( )
A. -1 B. 0 C. 1 D. 2
8.当时,下面的程序段结果是 ( )
A. 3 B. 7 C. 15 D. 17
9.下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( )
___________
A. B. C. D.
10.下列各数中最小的数是 ( )
A. B. C. D.
二、填空题 (每小题5分,共20分)
11.如图⑵程序框图箭头a指向①处时,输出 s=__________.
箭头a指向②处时,输出 s=__________.
12.此题程序运行结果为___________。
13.若输入的数字是“37”,输出的结果是________________.
14.2183 和1947的最大公约数是___________________.
三、解答题 (每小题10分,共30分)15.已知= 编写一个程序,对每输入的一个值,都得到相应的函数值.
16.用WHILE语句求的值。
17.设个人月收入在5000元以内的个人所得税档次为(单位: 元):
0%
10%
25%
设某人的月收入为元,试编一段程序,计算他应交的个人所得税.
18.求100~999中的水仙花数,所谓水仙花数是一个三位数,它的各位数字的立方和等于该数,例如153是一个水仙花数,因为.试编一段程序,找出所有的水仙花数.
第一章 算法初步测试题(B组)
一、选择题
1.在输入语句中,若同时输入多个变量,则变量之间的分隔符号是 ( )
A.逗号 B.空格 C.分号 D.顿号
2.以下条件表达示正确的是 ( )
A. B. C. D.
3.二进制数10111转化为五进制数是 ( )
A.41 B.25 C.21 D.43
4.在语句PRINT 3,3+2的结果是 ( )
A.3,3+2 B.3 5 C.3,5 D.3 2+3
5.用秦九韶算法在计算时,要用到的乘法和加法的次数分别为 ( )
A.4,3 B.6,4 C.4,4 D.3,4
6.下列输入语句正确的是 ( )
A.INPUT B.INPUT “”;,“”;
C.INPUT 2,3,4 D.INPUT
7.将表示成计算机程序表达式为了 ( )
A. B.
C. D.
8.
PRINT
END
以上程序输出的结果是 ( )
A.3,4 B. 4,4 C.3,3 D.4,3
9.三位七进制的数表示的最大的十进制的数是 ( )
A.322 B.332 C.342 D.352
10.INPUT
MOD 10
PRINT
END
若,则以上程序运行后的结果是 ( )
A.0.5 B.3 C.1.5 D.4.5
二、填空题
11.=_____________________.
12.一个完整的程序框图至少应该包含_________________________.
13.5280和2155的最大公约数是__________________________.
14.用二分法求方程的近似根,精确度为,则循环结构中止的条件是_______________.
三、解答题
15.用秦九韶算法计算函数在时的函数值.
16.铁路托运行李,从甲地到乙地,按规定每张客票托运行李不超过50㎏时,每千克0.2元,超过50㎏时,超过部分按每千克0.25元计算,画出计算行李价格的算法框图.
17.某次考试,满分100分,按规定者为良好,者为及格,小于60者不及格,画出当输入一个同学的成绩时,输出这个同学属于良好、及格还是不及格的程序框图.
18.输入3个数,输出其中最大的公约数,编程序完成上述功能.
19.编程序,求和
20.利用,编写程序求的近似值(精确到0.001).
第一章算法初步测试题(A组)
一、选择题 DBABA DBCAA
二、填空题11.5,15 12. 13.73 14.59
三、解答题
15.程序如下:
Input x
If x>=0 then
y=x*x-1
Else
y=2*x*x-5
End if
Print y
End
16. 程序如下:
i=0
s=0
While i<=63
s=s+2^i
i=i+1
Wend
Print s
End
17. 分析:设个人所得税为元,则
解: INPUT“请输入个人月收入X= ”;X
IF x>0 AND X<=1000 THEN
ELSE
IF x>1000 AND x<=3000 THEN
ELSE
IF x>3000 AND x<=5000 THEN
END IF
END IF
END IF
PRINT“个人月收入X=”;X
PRINT“个人所得税y=”;y
END
18.解: I=100
DO
A=I\100
B=(I-100*A)\10
C=I-A*100-B*10
IF I=A*A*A+B*B*B+C*C*C THEN
PRINT I
END IF
I=I+1
LOOP UNTIL I>999
END
第一章算法初步测试题(B组)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B C A A B C D
二、填空题
11. 75
12. 终端框、处理框
13. 5
14.
三、解答题
15. 解=,
∴,
∴,
,
,
即.
16. 程序框图:
17.程序框图:
18.解: INPUT m,n,k
r= m MOD n
WHILE r<>0
m=n
n=r
r= m MOD n
WEND
r= k MOD n
WHILE r<>0
k=n
n=r
r= k MOD n
WEND
PRINT n
END
19.解:s=0
n=1
t=1
WHILE n<=20
s=s+t
n=n+1
t=t * n
WEND
PRINT s
END
20.解:p=0
n=1
WHILE 4/n>0.001
IF n MOD 4=1 THEN
p=p+4/n
ELSE
p=p-4/n
END IF
n=n+2
WEND
PRINT p
END
>?
输入
开始
是
结束
输出
>?
否
是
开始
输入
除以2的余数
输出“是偶数”
是
输出“是奇数”
否
结束
第2题图
第3题图
否
满足条件?
否
是
循环体
AA
满足条件?
循环体
是
否
循环体
满足条件?
否
是
循环体
满足条件?
A
B
C
是
否
D
=2
=3
=4
=
=+2
=+4
PRINT “=”;d
第12题
INPUT x
IF x>9 AND x<100 THEN
a=x\10
b=x MOD 10
x=10*b+a
PRINT x
END IF
END
第13题程序
开始
i=1
s=0
s=s+i
i=i+1
i≤5
Y
①
②
a
N
结束
11题
输出s
开始
输入
输出
结束
是
否
开始
输入
输出良好
结束
输出及格
输出不及格
否
是
是
否
第1页(共23页
§1.1.1算法的概念
1、 基础梳理
1、算法的概念:在数学中,算法通常是指 。现在,算法通常可以编成 ,让计算机执行并解决问题。
2.计算机解决任何问题都依赖于算法,只有将解决问题的过程 ,并用计算机能够接受的“语言” ,计算机才能够 。
2、 合作探究
1、 你能举出更多的算法的例子吗?
2、 与一般的解决问题的过程相比,你认为算法最重要的特征是什么?
3、 自学检测
1、 跟根据算法的思想,用自然语言写出烧开水的过程。
2、 下列关于算法的说法中,,正确的有( )
①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是清楚的,不能有歧义;④算法执行后一定产生确定的结果.
A.1个 B.2个 C.3个 D.4个
3、现在河的岸边有三头牛和三只虎要过河,它们都会划船,只有一条船,船上一次只能载它们其中的两个,虎数大于牛数则虎就要吃牛,两者数目相等或是牛数大于虎数便相安无事。 设计安全渡河的算法。
4、 学生反馈
§1.1.1程序框图(第一课时)
一、基础梳理
1、完成下列表格:
图形符号 名称 功能
起止框(终端框) 表示一个算法的起始和结束
输入输出框 表示一个算法输入和输出的信息
处理框(执行框) 赋值、计算
判断框 判断某一条件是否成立,它有两个出口:“是”或“否”。条件成立时,程序沿着“是”这个分支走下去;当条件不成立时,程序沿着“否”这个分支进行。
流程线 连接程序框
连接点 当一个程序框图很大,一页纸写不下时,用来连接程序框图的两部分。一般在连接处标上相同的数字序号。
2、程序框图又称 ,是一种用 来表示算法的图形。
3、尽管算法千差万别,但它们都是由 、 、 这三种基本的逻辑结构构成的。
1、
二、合作探究
你能说出下列算法的功能吗?
三、自学检测
1、 在学案一中我们用自然语言写出了烧开水的过程,你能用程序框图表示这个过程吗?
四、学生反馈
2、
§1.1.1程序框图(第二课时)
一、基础梳理
1、在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件 有不同的流向,这种先根据条件做出判断,再决定执行哪种操作的结构叫 。
2、条件结构在程序框图中用判断框来表示,在判断框内写上条件,它有 个出口。
3、如下图是一个条件结构,当条件P成立时执行 框,P不成立时执行 框。
二、合作探究
在右图所示的条件结构中,能否既执行A框又执行B框?能否A框、B框都不执行?
三、自学检测
1、给计算机编写一个算法,输入一个自变量的值,求分段函数的函数值,并画出程序框图。
2、题1中当x取7,0,-5时,程序分别沿着哪条路线运行?请画出来。
四、学生反馈
§1.1.1程序框图(第三课时)
一、基础梳理
1、当型型循环结构在执行循环体之 ,对循环条件进行判断,当条件 时执行循环体, 时则停止循环,执行循环结构后面的步骤。
2、直到型循环结构在 之后,对循环条件进行判断,当条件 时执行循环体, 则停止循环,执行循环结构后面的步骤。
3、试说明计数变量和累加变量的作用。
二、合作探究
下面是描述描述一个饿汉吃饼的情况,如果饥饿的话就吃一张饼,直到吃饱为止。分别用当型和直到型两种循环结构进行描述。
[探究] 找出当型和直到型的区别
(1) 当 型:先判断条件,再执行循环体;
直到型:______________________________。
(2) 当型和直到型的条件_________。
(3) 当 型:满足条件时执行循环体;
直到型:____________________________。
三、自学检测
利用两种循环设计一个计算的算法,并画出程序框图。四、学生反馈
§1.2.1输入、输出语句和赋值语句(第一课时)
一、基础梳理
1、输入语句的一般格式:
2、输出语句的一般格式:
3、赋值语句的一般格式:
注意标点哦!
附:程序中常用符号
函数名 算术运算符
符号 LOG(x) SQR(x) ABS(x) ^ *,/ MOD,\ +,-
作用 lg(x) |x| 乘方 乘法,除法 求余数,求商 加法,减法
关系运算符 逻辑运算符
符号 = < > >= <= < , > AND OR NOT
作用 赋值 小于,大于 且 或 非
二、合作探究
1、“变量”和“表达式”有什么联系和区别?
2、你是怎么理解赋值语句中的“=”号的,它与“等于”号一样吗?
三、自学检测
1、已知y=x2-3x+1,编写程序,根据输入的x计算并输出y值。
四、学生反馈
课题:1.2.2条件语句(第二课时)
一、基础梳理
1、条件语句的一般格式:(实线框中填语句,虚线框中画框图)
IF-THEN-ELSE格式
IF-THEN格式
二、合作探究
条件结构中,有两个分支,能否两个分支都执行或两个分支都不执行?
三、自学检测
1、编写一个程序,输入3个数,找出其中最大的1个并输出。
四、学生反馈
课题:1.2.3循环语句(第三课时)
一、基础梳理
1、算法中的循环结构是由循环语句来实现的。对应于程序框图中的两种循环结构,一般程序设计语言中也有 型( 型)和 ( 型)两种语句结构。即WHILE语句和UNTIL语句。
(1)WHILE语句的一般格式是:(实线框中填语句,虚线框中画框图)
(2)UNTIL语句的一般格式是:
二、合作探究
试说明WHILE型循环与UNTIL型循环的区别和联系。
三、自学检测
1、设计一个计算的算法,画出程序框图,写出程序。
2、设计一个算法,求的值.,画出程序框图,写出程序。
四、学生反馈
课题:§1.3算法案例(第一课时)
一、基础梳理
1、辗转相除法是用于求 。它是由欧几里德在公元前300年左右首先提出的,因而又叫欧几里德算法。
2、所谓辗转相除法,就是对于给定的两个数,用 除以 。若余数不为零,则将 构成一对新数,继续上面的除法,直到大数被小数除尽,则这时 就是原来两个数的最大公约数。
二、合作探究
用当型循环结构构造算法,求两个正整数的最大公约数吗?试写出算法步骤、程序框图各程序。
三、自学检测
1、转相除法求下列各组数的最大公约数,并在自己编写的BASIC程序中验证。
(1)225;135 (2)98;196 (3)72;168 (4)153;119
四、学生反馈
课题:§1.3算法案例(第二课时)
一、基础梳理
1、更相减损术是我国古代数学专著 中介绍的一种求两个数的最大公约数的方法.其步骤是:第一步,任意给定两个正整数;判断它们是否都是偶数.若是,用2约简;若不是,执行第二步;第二步,以 ,接着把所得的 与 比较,并以大数减小数.继续这个操作,直到所得的数 为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数。
二、合作探究
把更相减损术与辗转相除法比较,你有什么发现?你能根据更相减损术设计程序,求两个正整数的最大公约数吗?
三、自学检测
1、用更相减损术求294与84最大公约数。
2、分别用辗转相除法和更相减损术求228与1995的最大公约数。
四、学生反馈
课题:§1.3算法案例(第三课时)
一、基础梳理
1、秦九韶算法是我国南宋数学家 在他的代表作 中提出的一种用于计算一元n次多项式的值的算法。
二、合作探究
用秦九韶算法求n次多项式当(是任意实数)时的值,需要多少次乘法运算,多少次加法运算?
三、自学检测
1、利用秦九韶算法计算
当时的值,并统计需要多少次乘法计算和多少次加法计算?
四、学生反馈
课题:§1.3算法案例(第四课时)
一、基础梳理
1、进位制是人们为了计数和运算方便而约定的记数系统.“满几进一”就是 ,几进制的基数就是
2、将k进制数化为十进制数的算法是:先把k进制数写成 的形式,再 .
3、将十进制数化为k进制数的算法是 ,即 ,直到商为零为止,然后 就是相应的k进制数.
二、合作探究
若表示一个k进制数,请你把它写成各位上数字与k的幂的乘积之和的形式。
三、自学检测
1、完成下列进位制的转化
①将十进制数4095化为七进制数;
②将21043(5)转化为十进制数。
2、将八进制数74(8)转化为二进制数。
四、学生反馈
第一章 算法初步测试题(A组)
一、选择题 (每小题5分,共50分)
1.已知直角三角形两直角边长为,,求斜边长的一个算法分下列三步:
①计算;②输入直角三角形两直角边长,的值;
③输出斜边长的值,其中正确的顺序是 ( )
A.①②③ B.②③① C.①③② D.②①③
2.给出以下一个算法的程序框图(如下图所示),该程序框图的功能是 ( )
A.求输出三数的最大数 B.求输出三数的最小数
C.将按从小到大排列 D.将按从大到小排列
3.右边的程序框图,能判断任意输入的数的奇偶性:其中判断框内的条件是( )
A. B. C. D.
4.将两个数=8,=7交换,使=7,=8,使用赋值语句正确的一组 ( )
A. B.
C. =,= D. =,=,=
5.下列给出的输入语句、输出语句和赋值语句
⑴输出语句INPUT ;; (2)输入语句INPUT =3
(3)赋值语句3=B (4)赋值语句A=B=2
则其中正确的个数是, ( )
A.0个 B. 1个 C. 2个 D. 3个
6.直到型循环结构为 ( )
7.下边程序执行后输出的结果是 ( )
A. -1 B. 0 C. 1 D. 2
8.当时,下面的程序段结果是 ( )
A. 3 B. 7 C. 15 D. 17
9.下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( )
___________
A. B. C. D.
10.下列各数中最小的数是 ( )
A. B. C. D.
二、填空题 (每小题5分,共20分)
11.如图⑵程序框图箭头a指向①处时,输出 s=__________.
箭头a指向②处时,输出 s=__________.
12.此题程序运行结果为___________。
13.若输入的数字是“37”,输出的结果是________________.
14.2183 和1947的最大公约数是___________________.
三、解答题 (每小题10分,共30分)15.已知= 编写一个程序,对每输入的一个值,都得到相应的函数值.
16.用WHILE语句求的值。
17.设个人月收入在5000元以内的个人所得税档次为(单位: 元):
0%
10%
25%
设某人的月收入为元,试编一段程序,计算他应交的个人所得税.
18.求100~999中的水仙花数,所谓水仙花数是一个三位数,它的各位数字的立方和等于该数,例如153是一个水仙花数,因为.试编一段程序,找出所有的水仙花数.
第一章 算法初步测试题(B组)
一、选择题
1.在输入语句中,若同时输入多个变量,则变量之间的分隔符号是 ( )
A.逗号 B.空格 C.分号 D.顿号
2.以下条件表达示正确的是 ( )
A. B. C. D.
3.二进制数10111转化为五进制数是 ( )
A.41 B.25 C.21 D.43
4.在语句PRINT 3,3+2的结果是 ( )
A.3,3+2 B.3 5 C.3,5 D.3 2+3
5.用秦九韶算法在计算时,要用到的乘法和加法的次数分别为 ( )
A.4,3 B.6,4 C.4,4 D.3,4
6.下列输入语句正确的是 ( )
A.INPUT B.INPUT “”;,“”;
C.INPUT 2,3,4 D.INPUT
7.将表示成计算机程序表达式为了 ( )
A. B.
C. D.
8.
END
以上程序输出的结果是 ( )
A.3,4 B. 4,4 C.3,3 D.4,3
9.三位七进制的数表示的最大的十进制的数是 ( )
A.322 B.332 C.342 D.352
10.INPUT
MOD 10
END
若,则以上程序运行后的结果是 ( )
A.0.5 B.3 C.1.5 D.4.5
二、填空题
11.=_____________________.
12.一个完整的程序框图至少应该包含_________________________.
13.5280和2155的最大公约数是__________________________.
14.用二分法求方程的近似根,精确度为,则循环结构中止的条件是_______________.
三、解答题
15.用秦九韶算法计算函数在时的函数值.
16.铁路托运行李,从甲地到乙地,按规定每张客票托运行李不超过50㎏时,每千克0.2元,超过50㎏时,超过部分按每千克0.25元计算,画出计算行李价格的算法框图.
17.某次考试,满分100分,按规定者为良好,者为及格,小于60者不及格,画出当输入一个同学的成绩时,输出这个同学属于良好、及格还是不及格的程序框图.
18.输入3个数,输出其中最大的公约数,编程序完成上述功能.
19.编程序,求和
20.利用,编写程序求的近似值(精确到0.001).
第一章算法初步测试题(A组)
一、选择题 DBABA DBCAA
二、填空题11.5,15 12. 13.73 14.59
三、解答题
15.程序如下:
Input x
If x>=0 then
y=x*x-1
Else
y=2*x*x-5
End if
Print y
End
16. 程序如下:
i=0
s=0
While i<=63
s=s+2^i
i=i+1
Wend
Print s
End
17. 分析:设个人所得税为元,则
解: INPUT“请输入个人月收入X= ”;X
IF x>0 AND X<=1000 THEN
ELSE
IF x>1000 AND x<=3000 THEN
ELSE
IF x>3000 AND x<=5000 THEN
END IF
END IF
END IF
PRINT“个人月收入X=”;X
PRINT“个人所得税y=”;y
END
18.解: I=100
DO
A=I\100
B=(I-100*A)\10
C=I-A*100-B*10
IF I=A*A*A+B*B*B+C*C*C THEN
PRINT I
END IF
I=I+1
LOOP UNTIL I>999
END
第一章算法初步测试题(B组)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B C A A B C D
二、填空题
11. 75
12. 终端框、处理框
13. 5
14.
三、解答题
15. 解=,
∴,
∴,
,
,
即.
16. 程序框图:
17.程序框图:
18.解: INPUT m,n,k
r= m MOD n
WHILE r<>0
m=n
n=r
r= m MOD n
WEND
r= k MOD n
WHILE r<>0
k=n
n=r
r= k MOD n
WEND
PRINT n
END
19.解:s=0
n=1
t=1
WHILE n<=20
s=s+t
n=n+1
t=t * n
WEND
PRINT s
END
20.解:p=0
n=1
WHILE 4/n>0.001
IF n MOD 4=1 THEN
p=p+4/n
ELSE
p=p-4/n
END IF
n=n+2
WEND
PRINT p
END
>?
输入
开始
是
结束
输出
>?
否
是
开始
输入
除以2的余数
输出“是偶数”
是
输出“是奇数”
否
结束
第2题图
第3题图
否
满足条件?
否
是
循环体
AA
满足条件?
循环体
是
否
循环体
满足条件?
否
是
循环体
满足条件?
A
B
C
是
否
D
=2
=3
=4
=
=+2
=+4
PRINT “=”;d
第12题
INPUT x
IF x>9 AND x<100 THEN
a=x\10
b=x MOD 10
x=10*b+a
PRINT x
END IF
END
第13题程序
开始
i=1
s=0
s=s+i
i=i+1
i≤5
Y
①
②
a
N
结束
11题
输出s
开始
输入
输出
结束
是
否
开始
输入
输出良好
结束
输出及格
输出不及格
否
是
是
否
第1页(共23页
