1.6利用三角函数测高分层练习-北师大版数学九年级下册(文字版,有答案)
文档属性
| 名称 | 1.6利用三角函数测高分层练习-北师大版数学九年级下册(文字版,有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 457.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 13:00:49 | ||
图片预览


文档简介
1.6利用三角函数测高分层练习-北师大版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,小明想测量斜坡旁一棵垂直于地面的树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,斜坡顶点到地面的垂直高度,则树的高度是( )
A.20 B.30 C.30 D.40
2.已知在△中,,,那么边的长等于( )
A.; B.; C.; D.;
3.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
A.9m B.6m C. D.
4.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
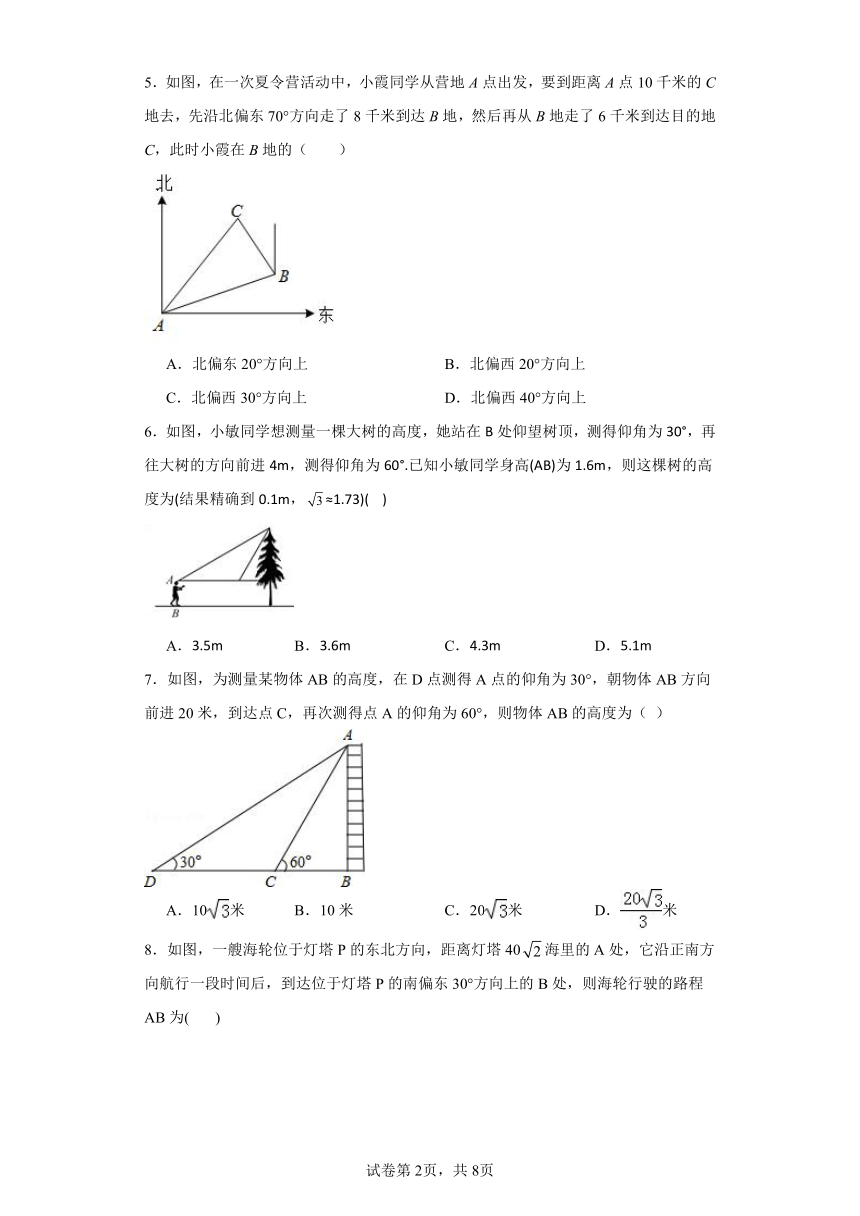
5.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
6.如图,小敏同学想测量一棵大树的高度,她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°.已知小敏同学身高(AB)为1.6m,则这棵树的高度为(结果精确到0.1m,≈1.73)( )
A.3.5m B.3.6m C.4.3m D.5.1m
7.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米 B.10米 C.20米 D.米
8.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )
A.(40+40)海里 B.(80)海里
C.(40+20)海里 D.80海里
9.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
10.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
二、填空题
11.如图,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i(即tanα)就是 .
12.如右图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,已知AB=6,AD=5,BC=4,则CE=
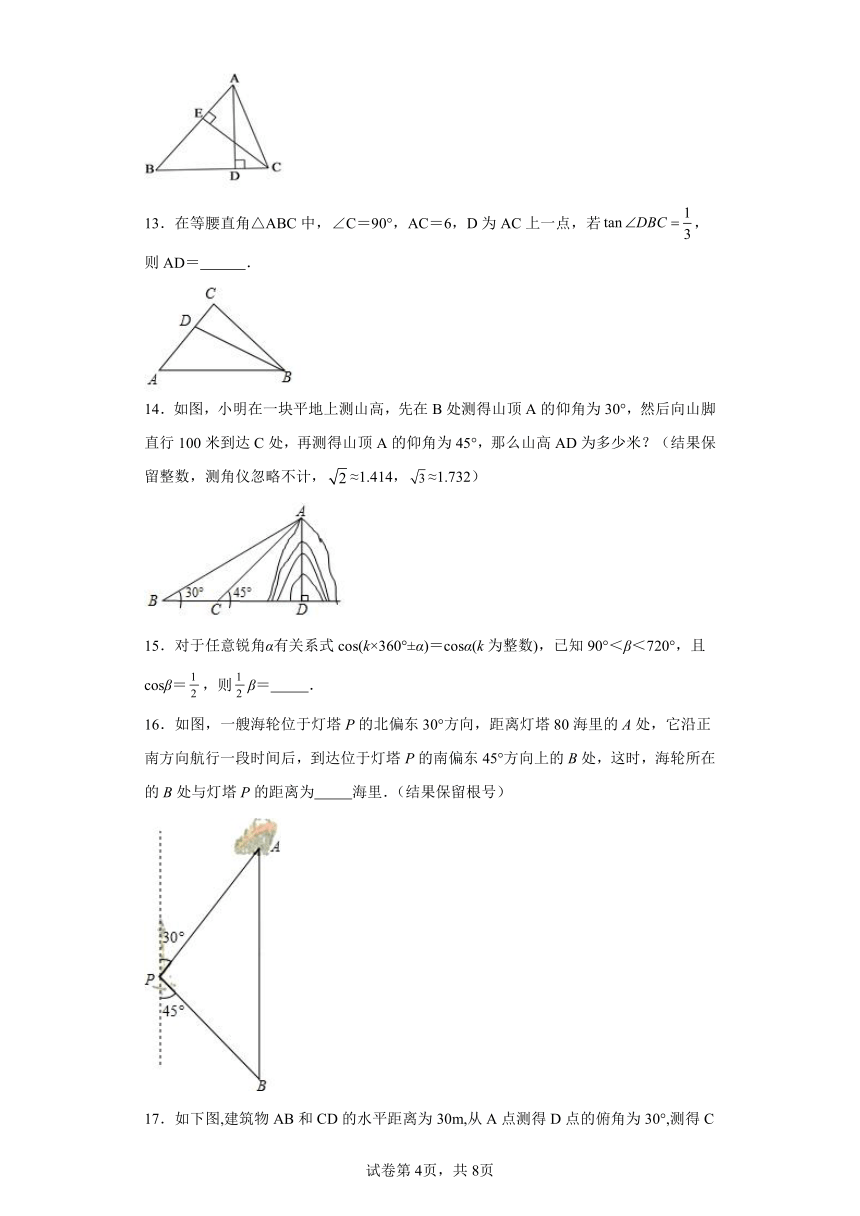
13.在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若,则AD= .
14.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为多少米?(结果保留整数,测角仪忽略不计,≈1.414,≈1.732)
15.对于任意锐角α有关系式cos(k×360°±α)=cosα(k为整数),已知90°<β<720°,且cosβ=,则β= .
16.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为 海里.(结果保留根号)
17.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为 m.
18.如图,小阳发现电线杆的影子落在土坡的坡面和地面上,量得,米,与地面成角,且此时测得米的影长为米,则电线杆的高度为 米.
19.已知:分别是的高,角平分线,,则的度数为 度.
20.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
三、应用题
21.如图,一条河的两岸平行,小刚在点处观测河对岸点的一棵树,测得;他沿河岸走了米到达点,此时观测河对岸点的另一棵树,测得,已知河宽米,求两棵树之间的距离.(结果保留根号)
22.如图,小林同学为了测量某世界名楼的高度,他站在G处仰望楼顶C,仰角为,走到点F处仰望楼顶C,仰角为,眼睛D、B离同一水平地面的高度为1.6米,米.请求出楼顶C离地面的高度约是多少米?(取1.732,取1.414,按四舍五入法将结果精确到0.1).
23.如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
24.钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
四、证明题
25.如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6,,求AB的长.
26.如图1,是H市人工天鹅湖畔的一尊雕塑A,雕塑A及另三个雕塑B、C、D的在湖岸边的平面分布如图2,某班综合实践小组分别在雕塑A、B两处设置观测点.在A处测得:雕塑B在西北方向,雕塑C在正北,雕塑D在北60°东;在B处测得:雕塑C在东北方向,雕塑D在正东.
(1)求证:AB=CB,AD=CD;
(2)已知AB=800米,求B、D之间的距离.(结果精确到1米)
(参考数据:≈1.73,≈1.41,≈2.45)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.C
5.B
6.D
7.A
8.A
9.C
10.C
11.0.6
12.
13.4
14.137.
15.210°或60°或240°或150°或330°或120°或300°
16.40
17.20m
18.(14+2)米
19.20或50
20.80
21.两棵树之间的距离为米
22.楼顶C离地面的高度约是48.9米.
23.m.
24.26m.
25.(1)略;(2)8.
26.(1)AB=CB,AD=CD;
(2)BD之间的距离为1544米.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,小明想测量斜坡旁一棵垂直于地面的树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,斜坡顶点到地面的垂直高度,则树的高度是( )
A.20 B.30 C.30 D.40
2.已知在△中,,,那么边的长等于( )
A.; B.; C.; D.;
3.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
A.9m B.6m C. D.
4.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
5.如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
6.如图,小敏同学想测量一棵大树的高度,她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°.已知小敏同学身高(AB)为1.6m,则这棵树的高度为(结果精确到0.1m,≈1.73)( )
A.3.5m B.3.6m C.4.3m D.5.1m
7.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米 B.10米 C.20米 D.米
8.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )
A.(40+40)海里 B.(80)海里
C.(40+20)海里 D.80海里
9.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
10.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10 m,楼高AB=24 m,则树CD高约为( )
A.5 m B.6 m C.7 m D.8 m
二、填空题
11.如图,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i(即tanα)就是 .
12.如右图所示,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,已知AB=6,AD=5,BC=4,则CE=
13.在等腰直角△ABC中,∠C=90°,AC=6,D为AC上一点,若,则AD= .
14.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为多少米?(结果保留整数,测角仪忽略不计,≈1.414,≈1.732)
15.对于任意锐角α有关系式cos(k×360°±α)=cosα(k为整数),已知90°<β<720°,且cosβ=,则β= .
16.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为 海里.(结果保留根号)
17.如下图,建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为 m.
18.如图,小阳发现电线杆的影子落在土坡的坡面和地面上,量得,米,与地面成角,且此时测得米的影长为米,则电线杆的高度为 米.
19.已知:分别是的高,角平分线,,则的度数为 度.
20.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
三、应用题
21.如图,一条河的两岸平行,小刚在点处观测河对岸点的一棵树,测得;他沿河岸走了米到达点,此时观测河对岸点的另一棵树,测得,已知河宽米,求两棵树之间的距离.(结果保留根号)
22.如图,小林同学为了测量某世界名楼的高度,他站在G处仰望楼顶C,仰角为,走到点F处仰望楼顶C,仰角为,眼睛D、B离同一水平地面的高度为1.6米,米.请求出楼顶C离地面的高度约是多少米?(取1.732,取1.414,按四舍五入法将结果精确到0.1).
23.如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
24.钟楼是云南大学的标志性建筑之一,某校教学兴趣小组要测量钟楼的高度,如图,他们在点A处测得钟楼最高点C的仰角为45°,再往钟楼方向前进至点B处测得最高点C的仰角为54°,AB=7m,根据这个兴趣小组测得的数据,计算钟楼的高度CD.(tan36°≈0.73,结果保留整数).
四、证明题
25.如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6,,求AB的长.
26.如图1,是H市人工天鹅湖畔的一尊雕塑A,雕塑A及另三个雕塑B、C、D的在湖岸边的平面分布如图2,某班综合实践小组分别在雕塑A、B两处设置观测点.在A处测得:雕塑B在西北方向,雕塑C在正北,雕塑D在北60°东;在B处测得:雕塑C在东北方向,雕塑D在正东.
(1)求证:AB=CB,AD=CD;
(2)已知AB=800米,求B、D之间的距离.(结果精确到1米)
(参考数据:≈1.73,≈1.41,≈2.45)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.B
4.C
5.B
6.D
7.A
8.A
9.C
10.C
11.0.6
12.
13.4
14.137.
15.210°或60°或240°或150°或330°或120°或300°
16.40
17.20m
18.(14+2)米
19.20或50
20.80
21.两棵树之间的距离为米
22.楼顶C离地面的高度约是48.9米.
23.m.
24.26m.
25.(1)略;(2)8.
26.(1)AB=CB,AD=CD;
(2)BD之间的距离为1544米.
答案第1页,共2页
答案第1页,共2页
