1.1锐角三角函数分层练习-北师大版数学九年级下册(文字版,有答案)
文档属性
| 名称 | 1.1锐角三角函数分层练习-北师大版数学九年级下册(文字版,有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 905.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 13:01:56 | ||
图片预览

文档简介
1.1锐角三角函数分层练习-北师大版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数上图象上有一点(在第一象限),函数的图象上有一点(在第二象限),是坐标原点,若,且,则( )
A. B. C. D.
2.在Rt中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
3.如图,格点图中每个小正方形的边长都是1,的顶点A,B,C都在格点上,则( )
A. B. C. D.
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
A. B. C. D.h﹣sinα
5.如图,在正方形中,点E为对角线上一点,连接,连接并延长至点F,使得,连接交于点G,若,则( )
A. B. C. D.
6.如图,四边形中,,,,分别为,的中点,则( )
A. B.2 C. D.
7.计算sin30°·cos60°的结果是( )
A. B. C. D.
8.如图,在菱形中,,,分别交、于点、,,连结,以下结论:①;②点到的距离是;③与的面积比为;④的面积为,其中一定成立的个数为( )
A.1 B.2 C.3 D.4
9.如图,在中,,于点,为上一点,使得.若,则( )
A. B. C. D.
10.在RtABC中,∠C=90°,已知∠A及边BC=a,则RtABC的斜边长应为( )
A.asinA B. C.acosA D.
二、填空题
11.某防洪堤坝的横断面是梯形,已知背水坡的坡长为,坡角为,则坝高为 .
12.如图,在菱形ABCD中,AB=6,∠B是锐角,点E是AB的中点,点F在BC上,BF=2,连结ED,EF,DF.若∠DEF=90°,则DF的长为 ,cos∠ABC的值为 .
13.如图,点E是矩形边上一点,于点F,若,则的长为 .
14.如图,点A、B、C为正方形网格中的3个格点,则sin∠ACB= .
15.(1)下列实数中:①,②,③6,④0,⑤-1.010010001,其中是无理数的有 (填序号).
(2)若一个n边形每一个内角都等于135°,则n= .
(3)如图,正比例函数与反比例函数的图象有一个交点,轴于点.平移直线,使其经过点,得到直线,则直线对应的函数表达式是 .
(4)如图,点在等边的内部,且,,,将线段绕点顺时针旋转得到,连接,则的值为 .
16.如图,在直角坐标平面内,O为原点,点A的坐标为,点B在第一象限内,,.则点B的坐标为 ; .
17.如图,在4×4的网格中,每个小正方形的边长均为1,的顶点A、B、C都在格点上,则的正切值为 .
18.已知为锐角,tan2sin 30,那么 °.
19.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于
20.如图,在中,,点D是的中点,连接,过点D作交于点E,若,,则的长为 .
三、应用题
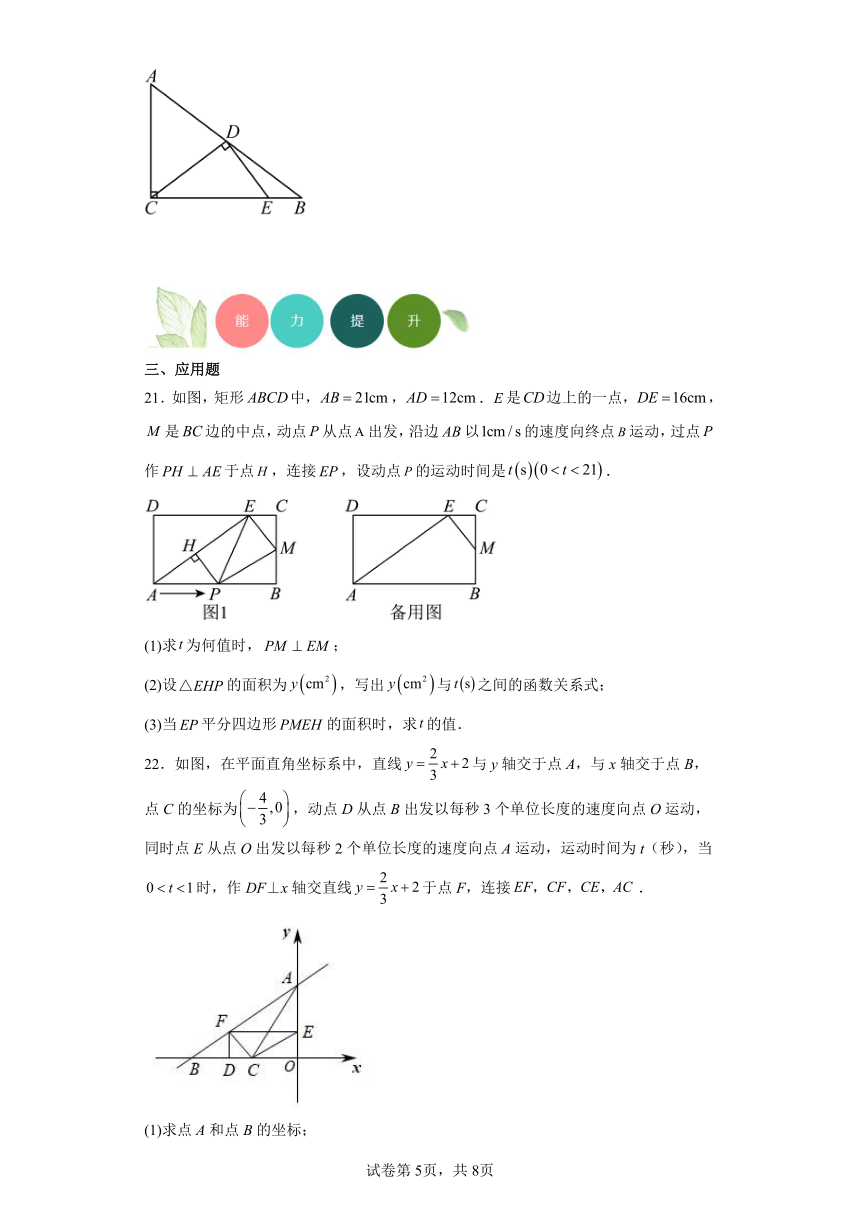
21.如图,矩形中,,是边上的一点,,是边的中点,动点从点出发,沿边以的速度向终点运动,过点作于点,连接,设动点的运动时间是.
(1)求为何值时,;
(2)设的面积为,写出与之间的函数关系式;
(3)当平分四边形的面积时,求的值.
22.如图,在平面直角坐标系中,直线与y轴交于点A,与x轴交于点B,点C的坐标为,动点D从点B出发以每秒3个单位长度的速度向点O运动,同时点E从点O出发以每秒2个单位长度的速度向点A运动,运动时间为t(秒),当时,作DF⊥x轴交直线于点F,连接.
(1)求点A和点B的坐标;
(2)求证:四边形是矩形;
(3)当与相似时,请直接写出t的值.
23.如图1,在平面直角坐标系中,直线:与轴交于点A,与轴交于点,直线与轴交于点,与直线交于,,.
(1)求直线的解析式.
(2)在直线上是否存在点,使的周长为?若存在,求出点的坐标,若不存在,请说明理由.
(3)如图2,连接,将沿直线翻折得到.若点为直线上一动点,在平面内是否存在点,使待以、、、为顶点的四边形为菱形,若存在,求出的坐标,若不存在,请说明理由.
24.如图1,在平面直角坐标系中,直线与直线相交于点,为线段上一动点(不与点重合),过点作轴交直线于点.与的重叠面积为.关于的函数图象如图2所示.
(1)的长为_______________;的面积为_______________.
(2)求关于的函数解析式,并直接写出自变量的取值范围.
25.综合与探究
问题情境:
数学活动课上,老师给出如下基础模型:如图①,已知,,过点C任作一条直线l(不与重合),过点A作于点D,过点B作于点E,当点A、B在直线l同侧时,易证(下列解题可直接用此结论).
(1)如图②,当点A、B在直线l异侧时,求证:.
模型应用:
在平面直角坐标系中,已知直线l:(k为常数,)与x轴交于点A,与y轴的负半轴交于点B,以AB为边、B为直角顶点作直角三角形且.
(2)若直线l经过点,当点C在第三象限时,点C的坐标为______.
(3)若点D是函数图象上的点,且轴,当点C在第四象限时,连接交y轴于点E,求点C、D的坐标(用含k的式子表示)及的长.
四、计算题
26.(1)计算:.
(2)解不等式:.
27.计算:.
五、证明题
28.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
29.如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=,求CP的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.C
3.C
4.A
5.A
6.C
7.A
8.B
9.C
10.B
11.30m
12. 8
13.6
14.
15. ② 8
16. /
17.
18.45
19.
20.15
21.(1)
(2)
(3)
22.(1),
(2)略
(3)t的值为
23.(1)
(2),或,
(3),或,或,或
24.(1),
(2)
25.(1)略
(2)
(3),,
26.(1) ; (2)
27.
28.(1)略;(2)
29.(1)略;(2)4.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数上图象上有一点(在第一象限),函数的图象上有一点(在第二象限),是坐标原点,若,且,则( )
A. B. C. D.
2.在Rt中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
3.如图,格点图中每个小正方形的边长都是1,的顶点A,B,C都在格点上,则( )
A. B. C. D.
4.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为( )
A. B. C. D.h﹣sinα
5.如图,在正方形中,点E为对角线上一点,连接,连接并延长至点F,使得,连接交于点G,若,则( )
A. B. C. D.
6.如图,四边形中,,,,分别为,的中点,则( )
A. B.2 C. D.
7.计算sin30°·cos60°的结果是( )
A. B. C. D.
8.如图,在菱形中,,,分别交、于点、,,连结,以下结论:①;②点到的距离是;③与的面积比为;④的面积为,其中一定成立的个数为( )
A.1 B.2 C.3 D.4
9.如图,在中,,于点,为上一点,使得.若,则( )
A. B. C. D.
10.在RtABC中,∠C=90°,已知∠A及边BC=a,则RtABC的斜边长应为( )
A.asinA B. C.acosA D.
二、填空题
11.某防洪堤坝的横断面是梯形,已知背水坡的坡长为,坡角为,则坝高为 .
12.如图,在菱形ABCD中,AB=6,∠B是锐角,点E是AB的中点,点F在BC上,BF=2,连结ED,EF,DF.若∠DEF=90°,则DF的长为 ,cos∠ABC的值为 .
13.如图,点E是矩形边上一点,于点F,若,则的长为 .
14.如图,点A、B、C为正方形网格中的3个格点,则sin∠ACB= .
15.(1)下列实数中:①,②,③6,④0,⑤-1.010010001,其中是无理数的有 (填序号).
(2)若一个n边形每一个内角都等于135°,则n= .
(3)如图,正比例函数与反比例函数的图象有一个交点,轴于点.平移直线,使其经过点,得到直线,则直线对应的函数表达式是 .
(4)如图,点在等边的内部,且,,,将线段绕点顺时针旋转得到,连接,则的值为 .
16.如图,在直角坐标平面内,O为原点,点A的坐标为,点B在第一象限内,,.则点B的坐标为 ; .
17.如图,在4×4的网格中,每个小正方形的边长均为1,的顶点A、B、C都在格点上,则的正切值为 .
18.已知为锐角,tan2sin 30,那么 °.
19.如图,△ABC的顶点都是正方形网格中的格点,则cos∠ACB等于
20.如图,在中,,点D是的中点,连接,过点D作交于点E,若,,则的长为 .
三、应用题
21.如图,矩形中,,是边上的一点,,是边的中点,动点从点出发,沿边以的速度向终点运动,过点作于点,连接,设动点的运动时间是.
(1)求为何值时,;
(2)设的面积为,写出与之间的函数关系式;
(3)当平分四边形的面积时,求的值.
22.如图,在平面直角坐标系中,直线与y轴交于点A,与x轴交于点B,点C的坐标为,动点D从点B出发以每秒3个单位长度的速度向点O运动,同时点E从点O出发以每秒2个单位长度的速度向点A运动,运动时间为t(秒),当时,作DF⊥x轴交直线于点F,连接.
(1)求点A和点B的坐标;
(2)求证:四边形是矩形;
(3)当与相似时,请直接写出t的值.
23.如图1,在平面直角坐标系中,直线:与轴交于点A,与轴交于点,直线与轴交于点,与直线交于,,.
(1)求直线的解析式.
(2)在直线上是否存在点,使的周长为?若存在,求出点的坐标,若不存在,请说明理由.
(3)如图2,连接,将沿直线翻折得到.若点为直线上一动点,在平面内是否存在点,使待以、、、为顶点的四边形为菱形,若存在,求出的坐标,若不存在,请说明理由.
24.如图1,在平面直角坐标系中,直线与直线相交于点,为线段上一动点(不与点重合),过点作轴交直线于点.与的重叠面积为.关于的函数图象如图2所示.
(1)的长为_______________;的面积为_______________.
(2)求关于的函数解析式,并直接写出自变量的取值范围.
25.综合与探究
问题情境:
数学活动课上,老师给出如下基础模型:如图①,已知,,过点C任作一条直线l(不与重合),过点A作于点D,过点B作于点E,当点A、B在直线l同侧时,易证(下列解题可直接用此结论).
(1)如图②,当点A、B在直线l异侧时,求证:.
模型应用:
在平面直角坐标系中,已知直线l:(k为常数,)与x轴交于点A,与y轴的负半轴交于点B,以AB为边、B为直角顶点作直角三角形且.
(2)若直线l经过点,当点C在第三象限时,点C的坐标为______.
(3)若点D是函数图象上的点,且轴,当点C在第四象限时,连接交y轴于点E,求点C、D的坐标(用含k的式子表示)及的长.
四、计算题
26.(1)计算:.
(2)解不等式:.
27.计算:.
五、证明题
28.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
29.如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=,求CP的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.C
3.C
4.A
5.A
6.C
7.A
8.B
9.C
10.B
11.30m
12. 8
13.6
14.
15. ② 8
16. /
17.
18.45
19.
20.15
21.(1)
(2)
(3)
22.(1),
(2)略
(3)t的值为
23.(1)
(2),或,
(3),或,或,或
24.(1),
(2)
25.(1)略
(2)
(3),,
26.(1) ; (2)
27.
28.(1)略;(2)
29.(1)略;(2)4.
答案第1页,共2页
答案第1页,共2页
