2.2二次函数的图像与性质分层练习-北师大版数学九年级下册(文字版,有答案)
文档属性
| 名称 | 2.2二次函数的图像与性质分层练习-北师大版数学九年级下册(文字版,有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 694.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 13:02:48 | ||
图片预览

文档简介
2.2二次函数的图像与性质分层练习-北师大版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于二次函数的图象及性质,下列说法正确的是( )
A.对称轴是直线 B.当时,y取得最小值,且最小值为
C.顶点坐标为 D.当时,y的值随x值的增大而增大
2.如图,已知抛物线的部分图像如图所示,抛物线与轴的交点在2和3之间(不含端点).则下列结论:①;②时,;③的最大值;④.其中正确的有( )个.
A.1 B.2 C.3 D.4
3.二次函数y=﹣x2+ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是( )
A.a=4 B.当x>2.5时,y随x的增大而减小
C.当x=﹣1时,b>5 D.当b=8时,函数最大值为10
4.如图,小红在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出同心圆与横线的一些交点.她发现这些点的位置有一定的规律,于是以圆心为原点,如图建立平面直角坐标系,相邻横线的间距为一个单位长度.则所描的点都在二次函数( )的图象上.
A. B. C. D.
5.二次函数y=(x-k)2与一次函数y=kx在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
6.对于抛物线,下列说法正确的是( )
A.图象开口向下,对称轴是直线 B.顶点坐标为
C.当时,函数取得最大值3 D.当时,y随x的增大而增大
7.抛物线的顶点坐标是( )
A. B. C. D.
8.二次函数y=ax +bx+c(a,b,c为常数)中的x与y的部分对应值如表所示:
x -1 0 1 3
y 3 3
下列结论:
(1)abc<0
(2)当x>1时,y的值随x值的增大而减小;
(3)16a+4b+c<0
(4)x=3是方程ax +(b-1)x+c=0的一个根;其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
9.将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上,如图所示,则两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)是( )
A.1 B.2 C.3 D.4
10.下列关于抛物线的说法,正确的是( )
A.开口向下 B.顶点坐标是
C.有最小值1 D.对称轴是直线
二、填空题
11.将抛物线先向左平移2个单位长度,再向上平移5个单位长度,所得抛物线的关系式为 .
12.若点三点在抛物线的图象上,则的大小关系是 (用“<”连接).
13.二次函数的图像的顶点坐标是 .
14.如图,抛物线y=ax2+bx与直线y=kx相交于O,A(3,2)两点,则不等式ax2+bx﹣kx<0的解集是 .
15.二次函数的图像经过原点,则a的值是 .
16.把抛物线的图象向右平移2个单位长度,再向下平移1个单位长度,则所得图象的顶点坐标为 .
17.抛物线沿着轴正方向看,在轴的左侧部分是 .(填“上升”或“下降”)
18.如图抛物线与轴交于,两点,与轴交于点,点是抛物线对称轴上任意一点,若点、、分别是、、的中点,连接,,则的最小值为 .
19.如图,矩形中,,点,分别是,上的点,且,若,,则的面积的最小值为 .
20.若点在二次函数()的图像上,则代数式的值为 .
三、应用题
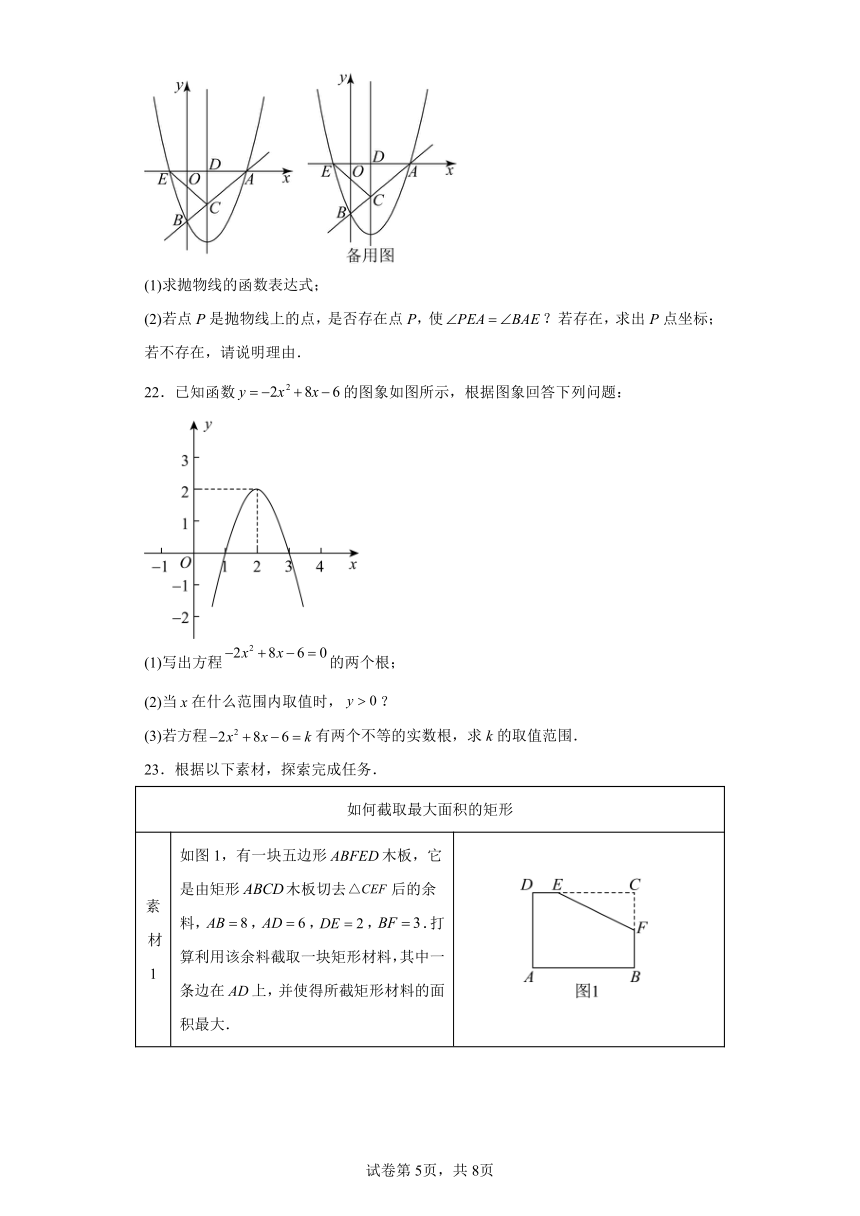
21.如图,抛物线与x轴正半轴交于点,与y轴交于点B,点C在直线上,过点C作轴于点,将沿所在直线翻折,点A恰好落在抛物线上的点E处.
(1)求抛物线的函数表达式;
(2)若点P是抛物线上的点,是否存在点P,使?若存在,求出P点坐标;若不存在,请说明理由.
22.已知函数的图象如图所示,根据图象回答下列问题:
(1)写出方程的两个根;
(2)当x在什么范围内取值时,?
(3)若方程有两个不等的实数根,求k的取值范围.
23.根据以下素材,探索完成任务.
如何截取最大面积的矩形
素材1 如图1,有一块五边形木板,它是由矩形木板切去后的余料,,,,.打算利用该余料截取一块矩形材料,其中一条边在上,并使得所截矩形材料的面积最大.
素材2 如图2,还有另一块木板,,,,,,且和之间的距离为6,点D到直线的距离为2,曲线是反比例函数图象的一部分.
问题解决
任务1 初步探究 在图1中,若截取的矩形有一边是,则截取的矩形面积是 . 若截取的矩形有一边是,则截取的矩形面积是 .
任务2 计算最大值 在图1中,发现可以截取出比任务1得到的面积更大的矩形,请你画出截取的矩形,并计算出该矩形面积的最大值.
任务3 拟定设计方案 在图2中建立合适的平面直角坐标系,求出曲线的函数表达式,利用该余料截取一块矩形材料,其中一条边在上,求所截矩形面积的最大
24.已知抛物线,
(1)若把该抛物线向右平移1个单位,再向上移动2个单位,则平移后抛物线解析式为 ;
(2)若把该抛物线绕它的顶点旋转,则旋转后的抛物线解析式为 .
25.如图,用长为的篱笆,一面利用墙(墙的最大可用长度为),围成中间隔有一道篱笆(平行于)的矩形花圃,设花圈的一边的长为,面积为,
(1)求y与x之间的函数关系式;
(2)如果围成的矩形的边的长度不小于.
①求自变量x的取值范围;
②求面积y的取值范围.
四、证明题
26.阅读材料,回答问题:
材料一 等于半径长的圆弧所对的圆心角叫做1弧度的角,用弧度作单位来度量角的制度叫做弧度制,弧度制和角度制都是度量角的常见方法,且二者之间可以互相转化.例如:一个完整的圆的弧度是,所以,则可以推知,……
材料二 在实际生活中经常会遇到角的旋转量不在0°-360°这个区间的情况,为了描述这种现实状况,我们把角的概念加以推广.任意一个角均可以表示为,其中k为整数,通过这个公式就可以将旋转量不在0°-360°这个区间的角度转化为旋转量在0°-360°这个区间的角.例如,则390°可以转化为30°,又例如,则可以转化为,
材料三 数学中,把称为正弦函数,把称为余弦函数.其中x为自变量,,为参数,当,,时,其函数图像如下图:
(1)设,,,按照从大到小正确排列a,b,c.
(2),,求证:
(3)“西气东输”,我国距离最长、口径最大的输气管道,西起塔里木盆地的轮南,东至上海.全线采用自动化控制,供气范围覆盖中原、华东、长江三角洲地区.在“西气东输”过程中,管线布置人员发现管线需要经过一个拐角为90°的拐弯峡谷,其宽为20m,峡谷的俯视图如图所示.现工作人员需要运输一根管道(图中AB)通过此峡谷,且运输时管道需保持水平.则在不损坏管道的情况下,此峡谷最大可以通过的多长的管道?
27.如图,在△ABC中,AD⊥BC于点D,E为BD上一点,过点E作EF⊥BC交AB于点F,过点F作FG⊥EF分别交AD,AC于点N,G,过点G作GH∥EF交BC于点H.
(1)求证:△AFG∽△ABC;
(2)若AD=3,BC=9,设EF的长度为x,四边形EFGH的面积为y,求y与x之间的函数表达式,并求y的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.D
4.B
5.B
6.C
7.C
8.B
9.B
10.C
11.(或)
12.
13.
14.0<x<3
15.1
16.
17.上升
18.
19.46
20.
21.(1)
(2)存在点P,使,P点坐标为或.
22.(1),
(2)
(3)
23.任务一:12,24;任务二:;任务三:函数表达式为,最大面积是42
24.
25.(1);
(2)①自变量的取值范围为;②面积的取值范围为.
26.(1)
(2)略
(3)
27.(1)略
(2)y=-3x2+9x (0<x<3),y最大值为
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.关于二次函数的图象及性质,下列说法正确的是( )
A.对称轴是直线 B.当时,y取得最小值,且最小值为
C.顶点坐标为 D.当时,y的值随x值的增大而增大
2.如图,已知抛物线的部分图像如图所示,抛物线与轴的交点在2和3之间(不含端点).则下列结论:①;②时,;③的最大值;④.其中正确的有( )个.
A.1 B.2 C.3 D.4
3.二次函数y=﹣x2+ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是( )
A.a=4 B.当x>2.5时,y随x的增大而减小
C.当x=﹣1时,b>5 D.当b=8时,函数最大值为10
4.如图,小红在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出同心圆与横线的一些交点.她发现这些点的位置有一定的规律,于是以圆心为原点,如图建立平面直角坐标系,相邻横线的间距为一个单位长度.则所描的点都在二次函数( )的图象上.
A. B. C. D.
5.二次函数y=(x-k)2与一次函数y=kx在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
6.对于抛物线,下列说法正确的是( )
A.图象开口向下,对称轴是直线 B.顶点坐标为
C.当时,函数取得最大值3 D.当时,y随x的增大而增大
7.抛物线的顶点坐标是( )
A. B. C. D.
8.二次函数y=ax +bx+c(a,b,c为常数)中的x与y的部分对应值如表所示:
x -1 0 1 3
y 3 3
下列结论:
(1)abc<0
(2)当x>1时,y的值随x值的增大而减小;
(3)16a+4b+c<0
(4)x=3是方程ax +(b-1)x+c=0的一个根;其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
9.将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上,如图所示,则两条抛物线、对称轴和y轴围成的图形的面积S(图中阴影部分)是( )
A.1 B.2 C.3 D.4
10.下列关于抛物线的说法,正确的是( )
A.开口向下 B.顶点坐标是
C.有最小值1 D.对称轴是直线
二、填空题
11.将抛物线先向左平移2个单位长度,再向上平移5个单位长度,所得抛物线的关系式为 .
12.若点三点在抛物线的图象上,则的大小关系是 (用“<”连接).
13.二次函数的图像的顶点坐标是 .
14.如图,抛物线y=ax2+bx与直线y=kx相交于O,A(3,2)两点,则不等式ax2+bx﹣kx<0的解集是 .
15.二次函数的图像经过原点,则a的值是 .
16.把抛物线的图象向右平移2个单位长度,再向下平移1个单位长度,则所得图象的顶点坐标为 .
17.抛物线沿着轴正方向看,在轴的左侧部分是 .(填“上升”或“下降”)
18.如图抛物线与轴交于,两点,与轴交于点,点是抛物线对称轴上任意一点,若点、、分别是、、的中点,连接,,则的最小值为 .
19.如图,矩形中,,点,分别是,上的点,且,若,,则的面积的最小值为 .
20.若点在二次函数()的图像上,则代数式的值为 .
三、应用题
21.如图,抛物线与x轴正半轴交于点,与y轴交于点B,点C在直线上,过点C作轴于点,将沿所在直线翻折,点A恰好落在抛物线上的点E处.
(1)求抛物线的函数表达式;
(2)若点P是抛物线上的点,是否存在点P,使?若存在,求出P点坐标;若不存在,请说明理由.
22.已知函数的图象如图所示,根据图象回答下列问题:
(1)写出方程的两个根;
(2)当x在什么范围内取值时,?
(3)若方程有两个不等的实数根,求k的取值范围.
23.根据以下素材,探索完成任务.
如何截取最大面积的矩形
素材1 如图1,有一块五边形木板,它是由矩形木板切去后的余料,,,,.打算利用该余料截取一块矩形材料,其中一条边在上,并使得所截矩形材料的面积最大.
素材2 如图2,还有另一块木板,,,,,,且和之间的距离为6,点D到直线的距离为2,曲线是反比例函数图象的一部分.
问题解决
任务1 初步探究 在图1中,若截取的矩形有一边是,则截取的矩形面积是 . 若截取的矩形有一边是,则截取的矩形面积是 .
任务2 计算最大值 在图1中,发现可以截取出比任务1得到的面积更大的矩形,请你画出截取的矩形,并计算出该矩形面积的最大值.
任务3 拟定设计方案 在图2中建立合适的平面直角坐标系,求出曲线的函数表达式,利用该余料截取一块矩形材料,其中一条边在上,求所截矩形面积的最大
24.已知抛物线,
(1)若把该抛物线向右平移1个单位,再向上移动2个单位,则平移后抛物线解析式为 ;
(2)若把该抛物线绕它的顶点旋转,则旋转后的抛物线解析式为 .
25.如图,用长为的篱笆,一面利用墙(墙的最大可用长度为),围成中间隔有一道篱笆(平行于)的矩形花圃,设花圈的一边的长为,面积为,
(1)求y与x之间的函数关系式;
(2)如果围成的矩形的边的长度不小于.
①求自变量x的取值范围;
②求面积y的取值范围.
四、证明题
26.阅读材料,回答问题:
材料一 等于半径长的圆弧所对的圆心角叫做1弧度的角,用弧度作单位来度量角的制度叫做弧度制,弧度制和角度制都是度量角的常见方法,且二者之间可以互相转化.例如:一个完整的圆的弧度是,所以,则可以推知,……
材料二 在实际生活中经常会遇到角的旋转量不在0°-360°这个区间的情况,为了描述这种现实状况,我们把角的概念加以推广.任意一个角均可以表示为,其中k为整数,通过这个公式就可以将旋转量不在0°-360°这个区间的角度转化为旋转量在0°-360°这个区间的角.例如,则390°可以转化为30°,又例如,则可以转化为,
材料三 数学中,把称为正弦函数,把称为余弦函数.其中x为自变量,,为参数,当,,时,其函数图像如下图:
(1)设,,,按照从大到小正确排列a,b,c.
(2),,求证:
(3)“西气东输”,我国距离最长、口径最大的输气管道,西起塔里木盆地的轮南,东至上海.全线采用自动化控制,供气范围覆盖中原、华东、长江三角洲地区.在“西气东输”过程中,管线布置人员发现管线需要经过一个拐角为90°的拐弯峡谷,其宽为20m,峡谷的俯视图如图所示.现工作人员需要运输一根管道(图中AB)通过此峡谷,且运输时管道需保持水平.则在不损坏管道的情况下,此峡谷最大可以通过的多长的管道?
27.如图,在△ABC中,AD⊥BC于点D,E为BD上一点,过点E作EF⊥BC交AB于点F,过点F作FG⊥EF分别交AD,AC于点N,G,过点G作GH∥EF交BC于点H.
(1)求证:△AFG∽△ABC;
(2)若AD=3,BC=9,设EF的长度为x,四边形EFGH的面积为y,求y与x之间的函数表达式,并求y的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.D
4.B
5.B
6.C
7.C
8.B
9.B
10.C
11.(或)
12.
13.
14.0<x<3
15.1
16.
17.上升
18.
19.46
20.
21.(1)
(2)存在点P,使,P点坐标为或.
22.(1),
(2)
(3)
23.任务一:12,24;任务二:;任务三:函数表达式为,最大面积是42
24.
25.(1);
(2)①自变量的取值范围为;②面积的取值范围为.
26.(1)
(2)略
(3)
27.(1)略
(2)y=-3x2+9x (0<x<3),y最大值为
答案第1页,共2页
答案第1页,共2页
