2.5二次函数与一元二次方程分层练习-北师大版数学九年级下册(文字版,有答案)
文档属性
| 名称 | 2.5二次函数与一元二次方程分层练习-北师大版数学九年级下册(文字版,有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 681.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-10 13:04:49 | ||
图片预览




文档简介
2.5二次函数与一元二次方程分层练习-北师大版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,抛物线的顶点为,与轴的一个交点坐标为.下列结论:①;②;③当时,;④若,则方程没有实数根.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
2.如图,二次函数:与一次函数:y=mx+n(m≠0)的图象交于A,B两点,则一元二次方程的解为( )
A. B., C., D.
3.如果关于的分式方程有整数解,且二次函数的图象与轴有交点,那么符合条件的所有整数的个数有( )
A.2个 B.3个 C.4个 D.5个
4.抛物线的顶点为,且经过点,其部分图象如图所示.对于此抛物线有如下四个结论:①;②;③;④方程的两根为.其中所有正确结论个数是( )
A.4个 B.3个 C.2个 D.1个
5.抛物线上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有( )个.
x … 0 1 …
y … 3 3 …
①当时,y随x的增大而减小.
②抛物线的对称轴为直线.
③当时,.
④方程一个正数解满足.
A.1 B.2 C.3 D.4
6.抛物线(是常数),,顶点坐标为.给出下列结论:①若点与点在该抛物线上,当时,则;②关于的一元二次方程无实数解,那么( )
A.①正确,②正确 B.①正确,②错误 C.①错误,②正确 D.①错误,②错误
7.抛物线y=ax2+bx+c(b<a<0)与x轴只有一个公共点,以下四个结论,正确的是( )
A.抛物线对称轴在y轴右侧
B.关于x的方程ax2+bx+c﹣2=0有实数根
C.a+b+c>0
D.的最小值为﹣1
8.如下表给出了二次函数中,,的一些对应值,则可以估计一元二次方程的一个近似解(精确到)为( )
A. B. C. D.
9.二次函数(、、是常数,且)的自变量与函数值的部分对应值如表:
1 2
3 4 3
有下列四个结论:①;②抛物线的对称轴是直线;③0和1是方程的两个根;④若,则.其中正确结论的个数是( ).
A.4 B.3 C.2 D.1
10.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下:
x 1.1 1.2 1.3 1.4 1.5 1.6
y -1.59 -1.16 -0.71 -0.24 0.25 0.76
则一元二次方程ax2+bx+c=0的一个解x满足条件( )
A.1.2<x<1.3 B.1.3<x<1.4 C.1.4<x<1.5 D.1.5<x<1.6
二、填空题
11.若二次函数的图象经过点(-1,0)和(3,0),则方程的解为 .
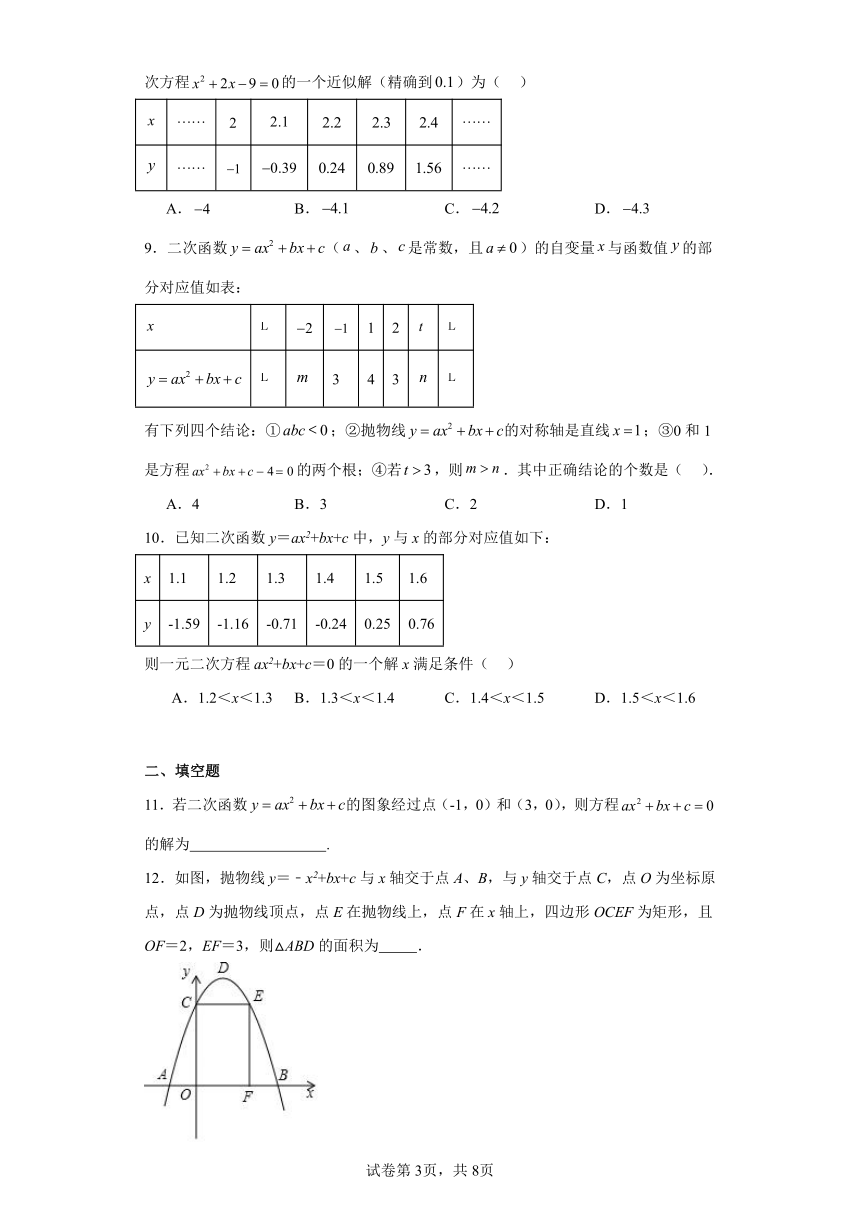
12.如图,抛物线y=﹣x2+bx+c与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,则△ABD的面积为 .
13.已知二次函数y=x2-3x+m(m是常数)的图象与x轴的一个交点为(1,0),则不等式x2-3x+m>0的解集是 .
14.方程有 个实数根.
15.如图,在平面直角坐标系xOy中,抛物线y=-2x2+bx+c与x轴交于A,B两点.若顶点C到x轴的距离为6,则线段AB的长为 .
16.如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
17.已知自变量为的二次函数经过、两点,若方程的一个根为,则其另一个根为 .
18.已知抛物线C1:y=x2-3x-10及抛物线C2:y=x2-(2a+2)x+a2+2a(a为常数),当-219.如图所示,已知二次函数的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线.直线与抛物线交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①;②;③;请写出所有正确选项的序号 .
20.我们约定:为函数的关联数,当其图像与坐标轴交点的横、纵坐标均为整时,该交点为“整交点”,若关联数为的函数图像与轴有两个整交点(为正整数),则这个函数图像上整交点的坐标为 .
三、应用题
21.某公园有一个小型喷泉,水柱从垂直于地面的喷水枪喷出,水柱落于地面的路径形状可以看作是抛物线的一部分.记喷出的水柱距喷水枪的水平距离为(单x位:m),距地面的垂直高度为y(单位:m),现测得x与y的几组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6 …
垂直高度y/m 0.7 1.6 2.3 2.8 3.1 3.2 3.1 …
请根据测得的数据,解决以下问题:
(1)在平面直角坐标系中,描出以表中各组对应数据为坐标的点,并画出该函数的图象;
(2)结合表中所给数据或所画图象,得出水柱最高点距离地面的垂直高度为 m;
(3)求所画图象对应的二次函数表达式;
(4)公园准备在水柱下方的地面上竖直安装一根高的石柱,使该喷水枪喷出的水柱恰好经过石柱顶端,则石柱距喷水枪的水平距离为 m.(注:不考虑石柱粗细等其他因素)
22.已知抛物线与轴交于两点(点在点左侧).
(1)抛物线对称轴为 ,点坐标为 ;
(2)当时,不等式的解集为 ;
(3)已知点,连接所得的线段与该抛物线有交点,求的取值范围.
23.前掷实心球是陕西省某市高中阶段学校招生体育考试的选考项目.小明投掷实心球训练,他尝试利用数学模型来研究实心球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,实心球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处,小明某次试投时的数据如图所示.
(1)根据图中信息,求出实心球路径所在抛物线的表达式.
(2)根据陕西省某市高中招生体育考试评分标准(男生),若实心球投球距离(实心球落地点与出手点的水平距离的长度)不小于,成绩为满分分.请通过计算,判断小明此次试投的成绩是否能达到满分.(参考数据:)
24.综合与探究
问题情境:
某商店购进一种冬季取暖的“小太阳”取暖器,每台进价为元,这种取暖器的销售价为每台元时,每周可售出台.
探究发现:
①销售定价每增加元时,每周的销售量将减少台;
②销售定价每降低元时,每周的销售量将增多台.
问题解决:
若商店准备把这种取暖器销售价定为每台元,每周销售获利为元.
(1)当时,这周的“小太阳”取暖器的销售量为______台,每周销售获利为______元.
(2)求与的函数关系式(不必写出的取值范围),并求出销售价定为多少时,这周销售“小太阳”取暖器获利最大,最大利润是多少?
(3)若该商店在某周销售这种“小太阳”取暖器获利元,求的值.
25.“急行跳远”是田径运动项目之一.运动员起跳后的腾空路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到落入沙坑的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.
某中学一名运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离 0 1 1.5 2 2.5 3
竖直高度 0 0.75 0.9375 1 0.9375 0.75
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系;
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系.记该运动员第一次训练落入沙坑点的水平距离为,第二次训练落入沙坑点的水平距离为,则________(填“”“”或“”).
四、计算题
26.某商场销售一种学生用计算器,进价为每台 20 元,售价为每台 30 元,每周可卖 160 台,如果每台售价每上涨 2 元,每周就会少卖 20 台,但厂家规定最高每台售价不能超过 33 元,设每台售价上x 元,每周的销售利润为 y 元.
(1)直接写出 y 与 x 之间的函数关系式;
(2)当计算器定价为多少元时,商场每周的利润恰好为 1680 元?
27.扶贫工作小组对果农进行精准扶贫,在果农与水果店之间牵线搭桥,帮助果农将一种有机生态水果拓宽了市场.已知某水果店从果农处直接以每千克24元的价格批发这种水果,然后在市场上销售.调查发现,若每千克销售价为41元,则每天可售出300千克,若每千克销售价每降低1元,每天可多售出60千克.
(1)当每千克销售价定为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计)
(2)为了让果农更快地将水果产品转化为收入,水果店在保证每天利润为6300元的情况下,可将每千克销售价定为多少元?
五、证明题
28.已知二次函数(a,m为然数,且).
(1)求证:不论a,m为何值,该函数的图象与x轴总有两个公共点;
(2)将该函数的图象绕原点旋转,则所得到的图象对应的函数表达式为________.
29.在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若抛物线与x轴的交点分别为A(x1,0),B(x2,0)且AB=2,求此抛物线的解析式;
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有且只有两个交点,求m的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.C
3.A
4.B
5.C
6.A
7.D
8.C
9.B
10.C
11.
12.8.
13.x<1或x>2
14.
15.2
16.m≥﹣4.
17.-5或3
18.<≤
19.①②③
20.或
21.(1)略
(2)3.2
(3)
(4)1或9
22.(1),
(2)或
(3)
23.(1)
(2)能达到满分
24.(1),;(2)当销售定价为元时,利润最大,最大为元;(3)当为或时,每周获利可达元
25.(1);
(2)<
26.(1)y=-10x2+60x+1600;(2)定价为32元时,最大利润为1680元.
27.(1)当每千克平均销售价为35元时,一天的利润最大,最大利润是7260元.
(2)每千克销售价定为31元.
28.(1)略
(2)
29.(1)略;(2)y=x2﹣8x+15;(3)m≥1
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,抛物线的顶点为,与轴的一个交点坐标为.下列结论:①;②;③当时,;④若,则方程没有实数根.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
2.如图,二次函数:与一次函数:y=mx+n(m≠0)的图象交于A,B两点,则一元二次方程的解为( )
A. B., C., D.
3.如果关于的分式方程有整数解,且二次函数的图象与轴有交点,那么符合条件的所有整数的个数有( )
A.2个 B.3个 C.4个 D.5个
4.抛物线的顶点为,且经过点,其部分图象如图所示.对于此抛物线有如下四个结论:①;②;③;④方程的两根为.其中所有正确结论个数是( )
A.4个 B.3个 C.2个 D.1个
5.抛物线上部分点的横坐标x和纵坐标y的对应值如下表,则下列说法中正确的有( )个.
x … 0 1 …
y … 3 3 …
①当时,y随x的增大而减小.
②抛物线的对称轴为直线.
③当时,.
④方程一个正数解满足.
A.1 B.2 C.3 D.4
6.抛物线(是常数),,顶点坐标为.给出下列结论:①若点与点在该抛物线上,当时,则;②关于的一元二次方程无实数解,那么( )
A.①正确,②正确 B.①正确,②错误 C.①错误,②正确 D.①错误,②错误
7.抛物线y=ax2+bx+c(b<a<0)与x轴只有一个公共点,以下四个结论,正确的是( )
A.抛物线对称轴在y轴右侧
B.关于x的方程ax2+bx+c﹣2=0有实数根
C.a+b+c>0
D.的最小值为﹣1
8.如下表给出了二次函数中,,的一些对应值,则可以估计一元二次方程的一个近似解(精确到)为( )
A. B. C. D.
9.二次函数(、、是常数,且)的自变量与函数值的部分对应值如表:
1 2
3 4 3
有下列四个结论:①;②抛物线的对称轴是直线;③0和1是方程的两个根;④若,则.其中正确结论的个数是( ).
A.4 B.3 C.2 D.1
10.已知二次函数y=ax2+bx+c中,y与x的部分对应值如下:
x 1.1 1.2 1.3 1.4 1.5 1.6
y -1.59 -1.16 -0.71 -0.24 0.25 0.76
则一元二次方程ax2+bx+c=0的一个解x满足条件( )
A.1.2<x<1.3 B.1.3<x<1.4 C.1.4<x<1.5 D.1.5<x<1.6
二、填空题
11.若二次函数的图象经过点(-1,0)和(3,0),则方程的解为 .
12.如图,抛物线y=﹣x2+bx+c与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,则△ABD的面积为 .
13.已知二次函数y=x2-3x+m(m是常数)的图象与x轴的一个交点为(1,0),则不等式x2-3x+m>0的解集是 .
14.方程有 个实数根.
15.如图,在平面直角坐标系xOy中,抛物线y=-2x2+bx+c与x轴交于A,B两点.若顶点C到x轴的距离为6,则线段AB的长为 .
16.如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是 .
17.已知自变量为的二次函数经过、两点,若方程的一个根为,则其另一个根为 .
18.已知抛物线C1:y=x2-3x-10及抛物线C2:y=x2-(2a+2)x+a2+2a(a为常数),当-2
20.我们约定:为函数的关联数,当其图像与坐标轴交点的横、纵坐标均为整时,该交点为“整交点”,若关联数为的函数图像与轴有两个整交点(为正整数),则这个函数图像上整交点的坐标为 .
三、应用题
21.某公园有一个小型喷泉,水柱从垂直于地面的喷水枪喷出,水柱落于地面的路径形状可以看作是抛物线的一部分.记喷出的水柱距喷水枪的水平距离为(单x位:m),距地面的垂直高度为y(单位:m),现测得x与y的几组对应数据如下:
水平距离x/m 0 1 2 3 4 5 6 …
垂直高度y/m 0.7 1.6 2.3 2.8 3.1 3.2 3.1 …
请根据测得的数据,解决以下问题:
(1)在平面直角坐标系中,描出以表中各组对应数据为坐标的点,并画出该函数的图象;
(2)结合表中所给数据或所画图象,得出水柱最高点距离地面的垂直高度为 m;
(3)求所画图象对应的二次函数表达式;
(4)公园准备在水柱下方的地面上竖直安装一根高的石柱,使该喷水枪喷出的水柱恰好经过石柱顶端,则石柱距喷水枪的水平距离为 m.(注:不考虑石柱粗细等其他因素)
22.已知抛物线与轴交于两点(点在点左侧).
(1)抛物线对称轴为 ,点坐标为 ;
(2)当时,不等式的解集为 ;
(3)已知点,连接所得的线段与该抛物线有交点,求的取值范围.
23.前掷实心球是陕西省某市高中阶段学校招生体育考试的选考项目.小明投掷实心球训练,他尝试利用数学模型来研究实心球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,实心球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处,小明某次试投时的数据如图所示.
(1)根据图中信息,求出实心球路径所在抛物线的表达式.
(2)根据陕西省某市高中招生体育考试评分标准(男生),若实心球投球距离(实心球落地点与出手点的水平距离的长度)不小于,成绩为满分分.请通过计算,判断小明此次试投的成绩是否能达到满分.(参考数据:)
24.综合与探究
问题情境:
某商店购进一种冬季取暖的“小太阳”取暖器,每台进价为元,这种取暖器的销售价为每台元时,每周可售出台.
探究发现:
①销售定价每增加元时,每周的销售量将减少台;
②销售定价每降低元时,每周的销售量将增多台.
问题解决:
若商店准备把这种取暖器销售价定为每台元,每周销售获利为元.
(1)当时,这周的“小太阳”取暖器的销售量为______台,每周销售获利为______元.
(2)求与的函数关系式(不必写出的取值范围),并求出销售价定为多少时,这周销售“小太阳”取暖器获利最大,最大利润是多少?
(3)若该商店在某周销售这种“小太阳”取暖器获利元,求的值.
25.“急行跳远”是田径运动项目之一.运动员起跳后的腾空路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从起跳到落入沙坑的过程中,运动员的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系.
某中学一名运动员进行了两次训练.
(1)第一次训练时,该运动员的水平距离x与竖直高度y的几组数据如下:
水平距离 0 1 1.5 2 2.5 3
竖直高度 0 0.75 0.9375 1 0.9375 0.75
根据上述数据,直接写出该运动员竖直高度的最大值,并求出满足的函数关系;
(2)第二次训练时,该运动员的竖直高度y与水平距离x近似满足函数关系.记该运动员第一次训练落入沙坑点的水平距离为,第二次训练落入沙坑点的水平距离为,则________(填“”“”或“”).
四、计算题
26.某商场销售一种学生用计算器,进价为每台 20 元,售价为每台 30 元,每周可卖 160 台,如果每台售价每上涨 2 元,每周就会少卖 20 台,但厂家规定最高每台售价不能超过 33 元,设每台售价上x 元,每周的销售利润为 y 元.
(1)直接写出 y 与 x 之间的函数关系式;
(2)当计算器定价为多少元时,商场每周的利润恰好为 1680 元?
27.扶贫工作小组对果农进行精准扶贫,在果农与水果店之间牵线搭桥,帮助果农将一种有机生态水果拓宽了市场.已知某水果店从果农处直接以每千克24元的价格批发这种水果,然后在市场上销售.调查发现,若每千克销售价为41元,则每天可售出300千克,若每千克销售价每降低1元,每天可多售出60千克.
(1)当每千克销售价定为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计)
(2)为了让果农更快地将水果产品转化为收入,水果店在保证每天利润为6300元的情况下,可将每千克销售价定为多少元?
五、证明题
28.已知二次函数(a,m为然数,且).
(1)求证:不论a,m为何值,该函数的图象与x轴总有两个公共点;
(2)将该函数的图象绕原点旋转,则所得到的图象对应的函数表达式为________.
29.在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若抛物线与x轴的交点分别为A(x1,0),B(x2,0)且AB=2,求此抛物线的解析式;
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有且只有两个交点,求m的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.C
3.A
4.B
5.C
6.A
7.D
8.C
9.B
10.C
11.
12.8.
13.x<1或x>2
14.
15.2
16.m≥﹣4.
17.-5或3
18.<≤
19.①②③
20.或
21.(1)略
(2)3.2
(3)
(4)1或9
22.(1),
(2)或
(3)
23.(1)
(2)能达到满分
24.(1),;(2)当销售定价为元时,利润最大,最大为元;(3)当为或时,每周获利可达元
25.(1);
(2)<
26.(1)y=-10x2+60x+1600;(2)定价为32元时,最大利润为1680元.
27.(1)当每千克平均销售价为35元时,一天的利润最大,最大利润是7260元.
(2)每千克销售价定为31元.
28.(1)略
(2)
29.(1)略;(2)y=x2﹣8x+15;(3)m≥1
答案第1页,共2页
答案第1页,共2页
